資料結構-八大排序演算法
目錄
最近在面試過程中,發現很多公司還是很注重基礎的,對於基本的排序要求掌握的比較紮實,能夠任意寫出各種排序,對各種排序效能進行比較,那就隨手總結一下吧。
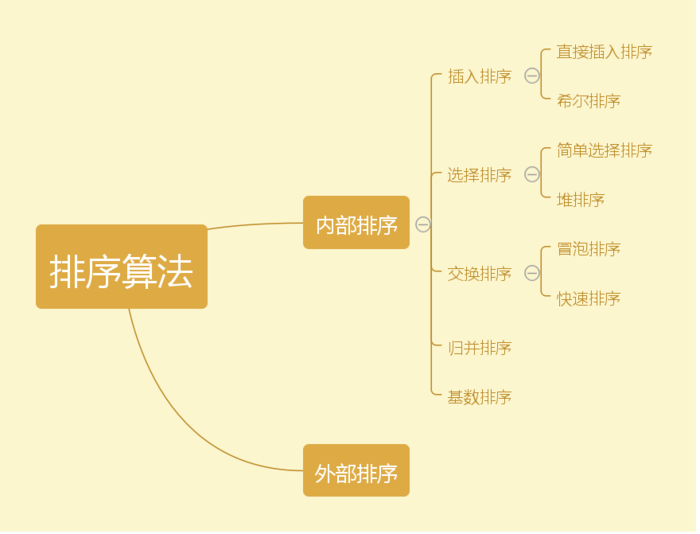
排序分類一覽
型別一 交換排序
氣泡排序
特點:穩定,每一次都會有一個數字到最終的位置
void swap(int &a,int &b)
{
int c = a;
a = b;
b = c;
}
void bubbleSort(int a[],int num)
{
for(int i=0;i<num-1;i++)
for(int j=0;j<num-i-1;j++)
if(a[j]>a[j+1])swap(a[j],a[j+1]);
}
快速排序
特點:不穩定,每次中間的數字會有序,如果資料量太大的話,可能會爆棧。

int qivotPosition(int a[],int low,int high) { int temp = a[low]; while(low<high) { while(low<high&&a[high]>=temp)high--; a[low] = a[high]; while(low<high&&a[low]<=temp)low++; a[high] = a[low]; } a[low] = temp; return low; } void quickSort(int a[],int low,int high) { if(low<high) { int qivot = qivotPosition(a,low,high); quickSort(a,low,qivot-1); quickSort(a,qivot+1,high); } }
比較
| 排序方法 | 平均時間複雜度 | 空間複雜度 | 穩定性 |
|---|---|---|---|
| 氣泡排序 | O(n2) | O(1) | 是 |
| 快速排序 | O(nlogn) | O(logn) | 否 |
型別二 插入排序
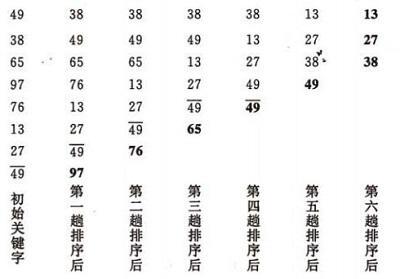
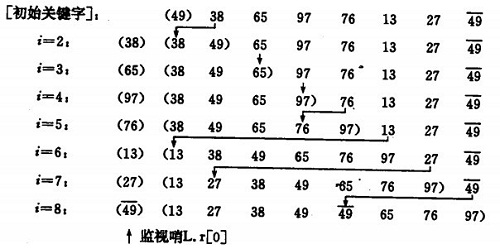
直接插入排序
特點:穩定,前面的一部分總是有序的,資料量比較小的時候適用。
void directInsert(int a[],int num)
{
int temp;
for(int i=0; i<num-1; i++)
{
if(a[i]>a[i+1])
{
int j;
temp = a[i+1];
for(j=i; temp<a[j]&&j>=0; j-- )
a[j+1] = a[j];
a[j+1] = temp;
}
}
}
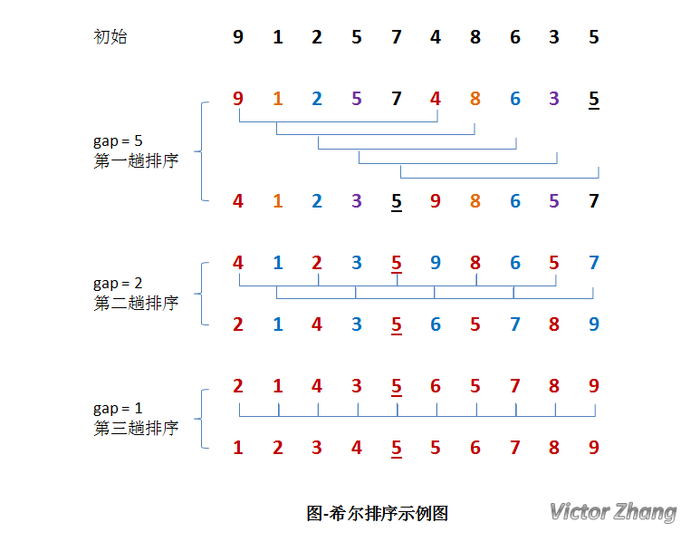
希爾排序
特點:不穩定,跨步長有序
void shellSort(int a[],int num)
{
int temp;
for(int dk=num/2; dk>=1; dk/=2)
for(int i=dk; i<=num; i++)
{
if(a[i]<a[i-dk])
{
temp = a[i];
int j;
for(j=i-dk;temp<a[j]&&j>=0;j-=dk)
a[j+dk] = a[j];
a[j+dk] = temp;
}
}
}
比較
| 排序方法 | 平均時間複雜度 | 空間複雜度 | 穩定性 |
|---|---|---|---|
| 直接插入排序 | O(n2) | O(1) | 是 |
| 希爾排序 | O(n1.3) | O(1) | 否 |
型別三 選擇排序
簡單選擇排序
特點:不穩定,每次都能有一個有序
void selectSort(int a[],int num)
{
for(int i=0;i<num-1;i++)
{
int min = i;
for(int j=i+1;j<num;j++)
if(a[j]<a[min])min = j; //記錄最小值
if(min!=i)
swap(a[i],a[min]);
}
}
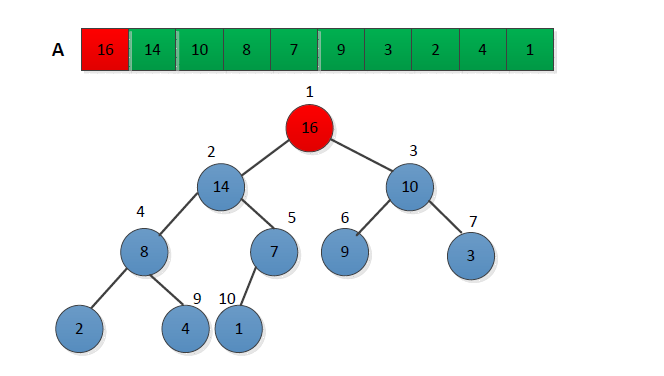
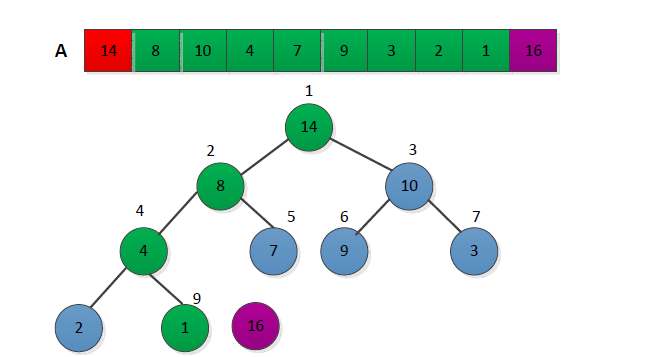
堆排
特點:堆排分為大頂堆和小頂堆,本例是以大頂堆為例,每次調整以後都可以找到最大值。最為重要的是堆排在最壞的情況下也可以保證O(nlogn)的時間複雜度,且空間複雜度為O(1)。資料量較大的時候比較適合選擇。
Note本例中的資料有特殊性 a[1]-a[num] 其中a[0]為臨時儲存容器
步驟如下
1.首先將序列構造成大根堆(位於根節點的一定是當前序列的最大值)
2.取出當前大頂堆的根節點,將其與序列末尾元素進行交換
3.對交換後的n-1個序列元素進行調整,使其滿足大頂堆的性質
4.重複2.3步驟,直至堆中只有1個元素為止
void adjustDown(int a[],int k,int num);
void buildMaxHeap(int a[],int num)
{
for(int i=num/2;i>0;i--)
adjustDown(a,i,num);
}
void adjustDown(int a[],int k,int num)
{
a[0] = a[k];
for(int i=2*k;i<=num;i*=2)
{
if(i<num&&a[i]<a[i+1])
i++;
if(a[0]>=a[i])break;
else
{
a[k] = a[i];
k = i;
}
}
a[k] = a[0];
}
void heapSort(int a[],int num)
{
buildMaxHeap(a,num);
for(int i=num;i>1;i--)
{
swap(a[i],a[1]);
adjustDown(a,1,i-1);
}
}
比較
| 排序方法 | 平均時間複雜度 | 空間複雜度 | 穩定性 |
|---|---|---|---|
| 簡答選擇排序 | O(n2) | O(1) | 否 |
| 堆排序 | O(nlogn) | O(1) | 否 |
型別四 歸併排序
歸併排序
特點:穩定,唯一速度快的排序中穩定的排序演算法,但付出了空間的代價。區域性有序,進而全域性有序。
int b[100];
void merge(int a[],int low,int mid,int high)
{
int i,j,k;
for(k=low;k<=high;k++)
{
b[k] = a[k];
}
for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++)
{
if(b[i]<=b[j])
a[k] = b[i++];
else
a[k] = b[j++];
}
while(i<=mid) a[k++] = b[i++]; //若第一個表未檢測完,複製
while(j<=high) a[k++] = b[j++]; //若第二個表未檢測完,複製
}
void mergeSort(int a[],int low,int high)
{
if(low<high)
{
int mid = (low+high)/2;
mergeSort(a,low,mid);
mergeSort(a,mid+1,high);
merge(a,low,mid,high);
}
}
比較
| 排序方法 | 平均時間複雜度 | 空間複雜度 | 穩定性 |
|---|---|---|---|
| 歸併排序 | O(nlogn) | O(n) | 是 |
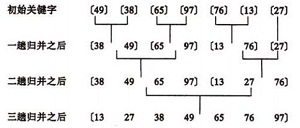
型別五 基數排序
基數排序
步驟如下:
1.分配:將L[i]中的元素取出,首先確定個位上的數字,根據該數字分配到與之序號相同的桶中。
2.收集:當序列中所有的元素都分配到對應的桶中,再按照順序依次將桶中的元素收整合新的一個待排序的序列L[];
3.對新形成的序列L[]重複執行分配和收集工作,對元素中的十位、百位…直到分配完該序列中的最高位,則排序結束。總體應用了一種“桶排”的思想。
比較
| 排序方法 | 平均時間複雜度 | 空間複雜度 | 穩定性 |
|---|---|---|---|
| 基數排序 | O(d(n+r)) | O® | 是 |
程式碼實現
上述排序的完整的可執行版本:
#include <iostream>
using namespace std;
//交換排序
//冒泡 穩定 每一次都會有一個數字到最終的位置
void swap(int &a,int &b)
{
int c = a;
a = b;
b = c;
}
void bubbleSort(int a[],int num)
{
for(int i=0;i<num-1;i++)
for(int j=0;j<num-i-1;j++)
if(a[j]>a[j+1])swap(a[j],a[j+1]);
}
//快排 不穩定 每次中間的數字會有序
//資料量中等時選用 數量太大可能會爆棧
int qivotPosition(int a[],int low,int high)
{
int temp = a[low];
while(low<high)
{
while(low<high&&a[high]>=temp)high--;
a[low] = a[high];
while(low<high&&a[low]<=temp)low++;
a[high] = a[low];
}
a[low] = temp;
return low;
}
void quickSort(int a[],int low,int high)
{
if(low<high)
{
int qivot = qivotPosition(a,low,high);
quickSort(a,low,qivot-1);
quickSort(a,qivot+1,high);
}
}
//插入排序
//直接插入 穩定 前面的一部分總是有序的
//資料量比較小的時候適用
void directInsert(int a[],int num)
{
int temp;
for(int i=0; i<num-1; i++)
{
if(a[i]>a[i+1])
{
int j;
temp = a[i+1];
for(j=i; temp<a[j]&&j>=0; j-- )
a[j+1] = a[j];
a[j+1] = temp;
}
}
}
//希爾排序 不穩定 跨步長有序
//步長的起始值為num/2
void shellSort(int a[],int num)
{
int temp;
for(int dk=num/2; dk>=1; dk/=2)
for(int i=dk; i<=num; i++)
{
if(a[i]<a[i-dk])
{
temp = a[i];
int j;
for(j=i-dk;temp<a[j]&&j>=0;j-=dk)
a[j+dk] = a[j];
a[j+dk] = temp;
}
}
}
//選擇排序 不穩定
//簡單選擇排序 每次都能有一個有序
void selectSort(int a[],int num)
{
for(int i=0;i<num-1;i++)
{
int min = i;
for(int j=i+1;j<num;j++)
if(a[j]<a[min])min = j; //記錄最小值
if(min!=i)
swap(a[i],a[min]);
}
}
//堆排 因為最後的交換 所以也是不穩定排序
//分為大頂堆和小頂堆 本例以大頂堆為例 每次調整之後都可以找到最大值
//本例中的資料有特殊性 a[1]-a[num] 其中a[0]為臨時儲存容器 所以陣列宣告需要a[num+1]
void adjustDown(int a[],int k,int num);
void buildMaxHeap(int a[],int num)
{
for(int i=num/2;i>0;i--)
adjustDown(a,i,num);
}
void adjustDown(int a[],int k,int num)
{
a[0] = a[k];
for(int i=2*k;i<=num;i*=2)
{
if(i<num&&a[i]<a[i+1])
i++;
if(a[0]>=a[i])break;
else
{
a[k] = a[i];
k = i;
}
}
a[k] = a[0];
}
void heapSort(int a[],int num)
{
buildMaxHeap(a,num);
for(int i=num;i>1;i--)
{
swap(a[i],a[1]);
adjustDown(a,1,i-1);
}
}
//歸併排序 穩定排序 區域性有序,進而全域性有序
int b[100];
void merge(int a[],int low,int mid,int high)
{
int i,j,k;
for(k=low;k<=high;k++)
{
b[k] = a[k];
}
for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++)
{
if(b[i]<=b[j])
a[k] = b[i++];
else
a[k] = b[j++];
}
while(i<=mid) a[k++] = b[i++]; //若第一個表未檢測完,複製
while(j<=high) a[k++] = b[j++]; //若第二個表未檢測完,複製
}
void mergeSort(int a[],int low,int high)
{
if(low<high)
{
int mid = (low+high)/2;
mergeSort(a,low,mid);
mergeSort(a,mid+1,high);
merge(a,low,mid,high);
}
}
int main()
{
int num;
int a[100];
/*
//堆排的輸入輸出
while(cin>>num)
{
for(int i=1;i<=num;i++)
cin>>a[i];
heapSort(a,num);
for(int i=1;i<=num;i++)
cout<<a[i]<<" ";
cout<<endl;
}*/
while(cin>>num)
{
//cin>>num; //一個數組的長度
for(int i=0;i<num;i++)
{
cin>>a[i];
}
//bubbleSort(a,num);
//quickSort(a,0,num-1);
//directInsert(a,num);
//shellSort(a,num);
//selectSort(a,num);
mergeSort(a,0,num-1);
for(int i=0;i<num;i++)
cout<<a[i]<<" ";
cout<<endl;
}
return 0;
}
效能對比
其中有幾個演算法比較特殊,歸併排序是唯一一個效率較高,卻穩定的演算法,因為它付出了空間的代價;堆排序與歸併的最好、最差時間複雜度都可以是O(nlogn),且堆排的空間複雜度僅為O(1)。