2. 程式人生 > >第四章圖演算法總結

第四章圖演算法總結

阿新 • • 發佈：2018-12-29

該部落格原地址http://blog.csdn.net/ntt5667781/article/details/52743342

其實就是對書上的內容做了個總結

在開始各類圖演算法之前，先將圖的結構進行分類。 
圖的表示，在實際實現過程中，有以下幾種基本的方式可以來表示圖。 
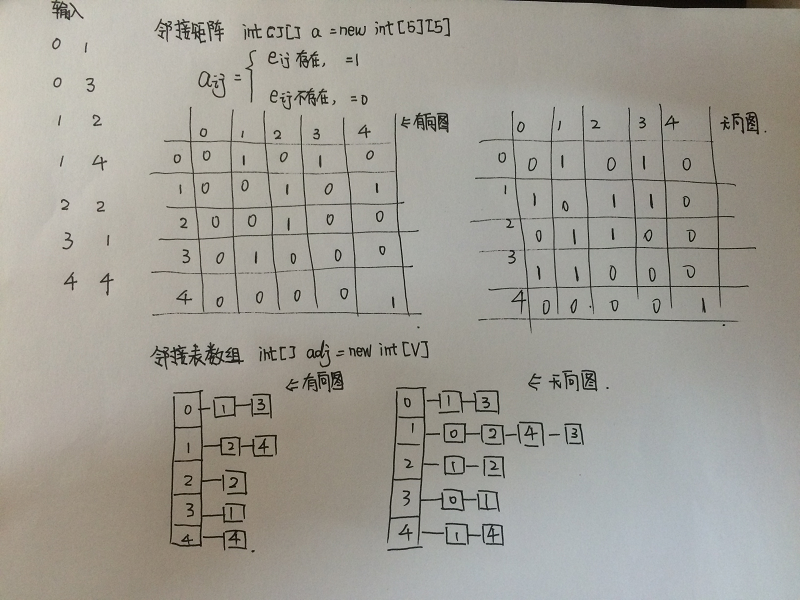
1） 鄰接矩陣：對於較小或者中等規模的圖的構造較為適用，因為需要V*V大小的空間。 
2） 邊的陣列：使用一個簡單的自定義edge類，還有兩個變數，分別代表邊的兩個端點編號，實現簡單，但是在求每個點的鄰接點的時候實現較為困難。 
3） 鄰接表陣列：較為常用，使用一個以頂點為索引的陣列，陣列每個元素都是和該頂點相鄰的頂點列表，這種陣列佔空間相對於鄰接矩陣少了很多，並且能很好的找到某個給定點的所有鄰接點。 

 
按照圖中邊的方向將圖分成有向圖和無向圖： 
1）無向圖：圖中的邊沒有方向。 
2）有向圖：圖中的邊有方向。 
對於有向圖和無向圖的具體實現表示可以使用前面介紹的三種方法，兩種圖在表示的時候大部分的實現程式碼都是一致的。 
普通無向圖的鄰接陣列表示方法的具體實現程式碼：

public class Graph {
    private int V;  //圖中的頂點數目
    private int E;  //圖中的邊數目
    private List<Integer>[] adj;  //鄰接陣列
    private int[][] a;   //鄰接矩陣
    public
 
 CreatGraph(int V) {  
        this.E = 0;
        this.V = V;
        adj = new ArrayList[V];
        a=new int[V][V];
        for (int i = 0; i < V; i++) 
            adj[i] = new ArrayList<>();
    }
    //由於無向圖中的邊是沒有方向的，所以新增邊的時候需要在邊的兩個頂點對應的鄰接列表中都新增頂點資訊。
    public void addEdge(int v1, int v2) { 
        a[v1][v2]=1
 
;
        a[v2][v1]=1;
        adj[v1].add(v2);
        adj[v2].add(v1);
        E++;
    }

    public int V() {
        return V;
    }

    public int E() {
        return E;
    }
    //鄰接陣列返回給定點的所有鄰接點
    public List<Integer> adj(int i) {
        return adj[i];
    }
    //鄰接矩陣返回給定點的所有鄰接點
    public List<Integer> adj1(int i){
    List<Integer> list=new ArrayList<>();
    int[] adj1=new int[V];
    adj1=a[i];
    for(int v:adg1)
        if(v!+0)list.add(v);
    return list; 
    }
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43

無權有向圖的具體實現程式碼：

public class DirectedGraph {
    private int V;  //圖中的頂點數目
    private int E;  //圖中的邊數目
    private List<Integer>[] adj;  //鄰接陣列
    private int[][] a;   //鄰接矩陣

    public DirectedGraph(int V) {
        this.E = 0;
        this.V = V;
        adj = new ArrayList[V];
        a=new int[V][V];
        for (int i = 0; i < V; i++) 
            adj[i] = new ArrayList<>();
    }
    //由於無向圖中的邊是有方向的，所以新增邊的時候需要只需要在起始點的鄰接列表中新增頂點資訊。
    public void addEdge(int v1, int v2) { 
        a[v1][v2]=1;
        adj[v1].add(v2);
        E++;
    }

    public int V() {
        return V;
    }

    public int E() {
        return E;
    }
    //鄰接陣列返回給定點的所有鄰接點
    public List<Integer> adj(int i) {
        return adj[i];
    }
    //鄰接矩陣返回給定點的所有鄰接點
    public List<Integer> adj1(int i){
    List<Integer> list=new ArrayList<>();
    int[] adj1=new int[V];
    adj1=a[i];
    for(int v:adg1)
        if(v!+0)list.add(v);
    return list; 
    }   
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42

一 圖的遍歷演算法：

介紹兩種比較基礎的圖遍歷演算法，廣度優先搜尋和深度優先搜尋。 
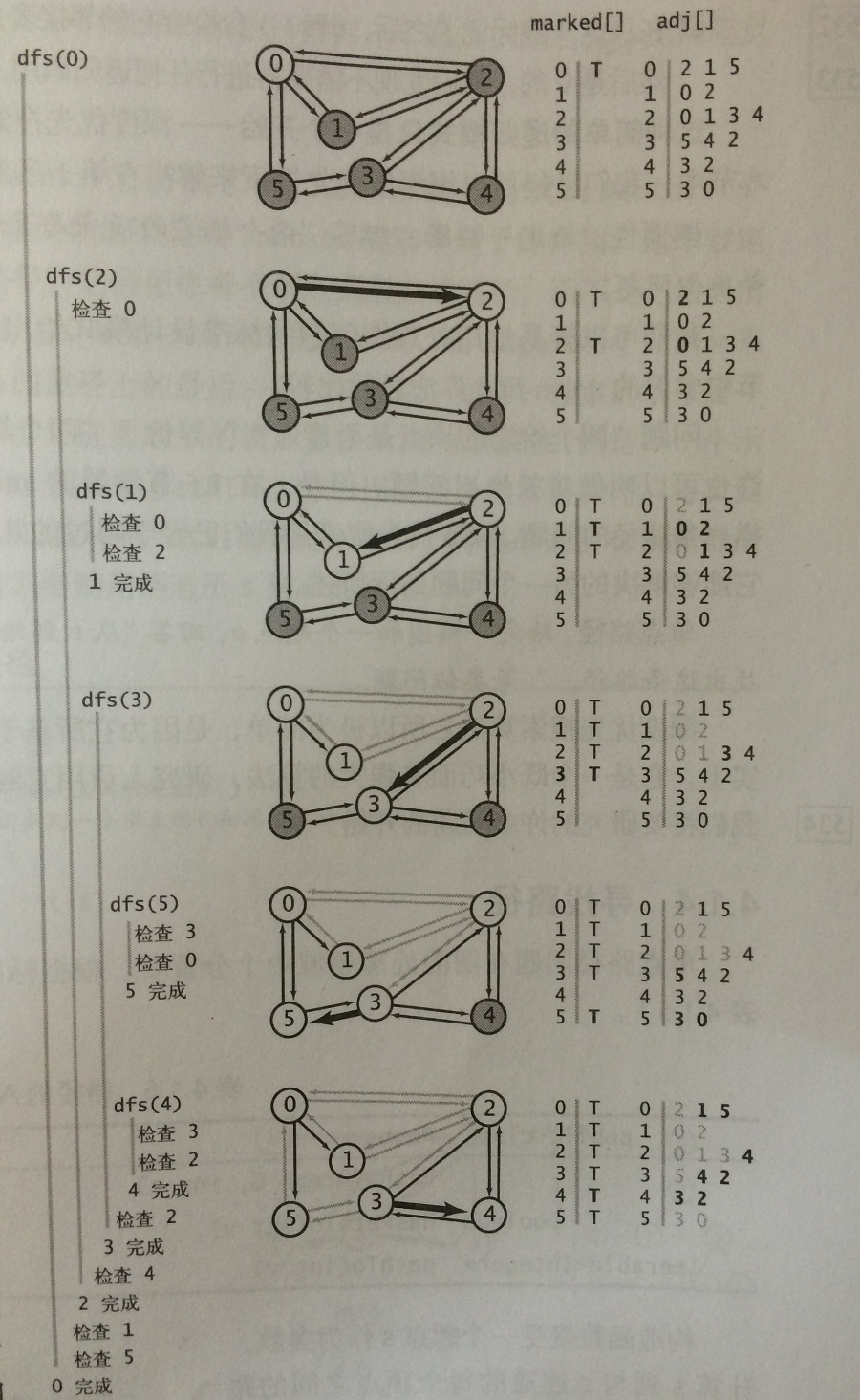
1）深度優先搜尋：這是一種典型的遞迴演算法用來搜尋圖（遍歷所有的頂點）； 
思想：從圖的某個頂點i開始，將頂點i標記為已訪問頂點，並將訪問頂點i的鄰接列表中沒有被標記的頂點j，將頂點j標記為已訪問，並在訪問頂點j的鄰接列表中未被標記的頂點k依次深度遍歷下去，直到某個點的所有鄰接列表中的點都被標記為已訪問後，返回上層。重複以上過程直到圖中的所有頂點都被標記為已訪問。 
深度優先遍歷和樹的先序訪問非常類似，儘可能深的去訪問節點。深度優先遍歷的大致過程（遞迴版本）： 
a）在訪問一個節點的時候，將其設定為已訪問。 
b）遞迴的訪問被標記頂點的鄰接列表中沒有被標記的所有頂點 
（非遞迴版本）: 
圖的非遞迴遍歷我們藉助棧來實現。 
a）如果棧為空，則退出程式，否則，訪問棧頂節點，但不彈出棧點節點。 
b）如果棧頂節點的所有直接鄰接點都已訪問過，則彈出棧頂節點，否則，將該棧頂節點的未訪問的其中一個鄰接點壓入棧，同時，標記該鄰接點為已訪問，繼續步驟a。 
該演算法訪問頂點的順序是和圖的表示有關的，而不只是和圖的結構或者是演算法有關。

深度優先探索是個簡單的遞迴演算法(當然藉助棧也可以實現非遞迴的版本)，但是卻能有效的處理很多和圖有關的任務，比如： 
a) 連通性：ex:給定的兩個頂點是否聯通 or 這個圖有幾個聯通子圖。 
b) 單點路徑：給定一幅圖和一個固定的起點，尋找從s到達給定點的路徑是否存在，若存在，找出這條路徑。

尋找路徑： 
為了實現這個功能，需要在上面實現的深度優先搜尋中中增加例項變數edgeTo[]，它相當於繩索的功能，這個陣列可以找到從每個與起始點聯通的頂點回到起始點的路徑（具體實現的思路非常巧妙： 從邊v-w第一次訪問w的時候，將edgeTo[w]的值跟新為v來記住這條道路，換句話說，v-w是從s到w的路徑上最後一條已知的邊，這樣搜尋結果就是一條以起始點為根結點的樹，也就是edgeTo[]是個有父連結表示的樹。）

深度優先搜尋的遞迴實現版本和非遞迴版本（遞迴是接住了遞迴中的隱藏棧來實現的。非遞迴，藉助棧實現）

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class DepthFirstSearch {
    //用來記錄頂點的標記狀態 true表示為已訪問，false表示為未被訪問。
    private boolean[] marked; 
    private int count;  
    //用來記錄頂點索引所對應的父結點，假設遍歷是從s到達的t那麼edgeTo[s所對的所用]=t;
    private int[] edgeTo; 
    //起始點
    private int s;  
    private Deque<Integer> dq=new Deque<>();

    public DepthFirstSearch(Graph G, int s) {
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];
        this.s = s; 
        dq.push(s);
        dfs(G, s);
    }

    //遞迴形式實現
    public void dfs(Graph G, int s) { 
        marked[s] = true;
        count++;
        for (int temp : G.adj(s))
            if (!marked[temp]) {
                edgeTo[temp] = s;
                dfs(G, temp);
            }
    }
    //非遞迴形式實現
    private void dfs(Graph G){
    while(!dp.isEmpty()){
        s=dp.peek();
        needPop=true;
        marked[s] = true;
        for (int temp : G.adj(s))
            if (!marked[temp]) {
                dp.push(temp);
                edgeTo[temp] = s;
                needPop=false;
                break;
            }
        }
        if(needPop)
        dp.pop();
    }
    public boolean hasPathTo(int v) {
        return marked[v];
    }

    public List<Integer> pathTo(int v) {
        if (hasPathTo(v))
            return null;
        List<Integer> list = new ArrayList<>();
        v = edgeTo[v];
        while (v != s) {
            list.add(v);
            v = edgeTo[v];
        }
        list.add(s);
        Collections.reverse(list);
        return list;
    }

    public int count() {
        return count;
    }
    public static void main(String[] args){
        int V = 0,E = 0;
        Graph G=new Graph(V,E);
        int s=0;
         DepthFirstSearch dfs=new  DepthFirstSearch(G,s);
         for(int v=0;v<G.V();v++){
             if(dfs.hasPathTo(v))
                 for(int x:dfs.pathTo(v))
                     if(x==s)
                         System.out.print(x);
                     else
                         System.out.print("-"+x);
             System.out.println();
             }
    }
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86

深度優先搜尋的實現軌跡（選取頂點0為起始頂點） 
已經使用DFS解決了一些問題，DFS其實還可以解決很多在無向圖中的基礎性問題，譬如： 
1）計算圖中的連通分支的數量；

public class ConnectComponent {
    private boolean[] marked;
    private int[] id;  //標記結點所在的連通分支編號
    private int count; //計算連通分支的個數

    public ConnectComponent(Graph G) {
        marked = new boolean[G.V()];
        id = new int[G.V()];
        for (int s = 0; s < G.V(); s++) {
            if (!marked[s]) {
                dfs(G, s);
                count++;
            }
        }
    }

    public void dfs(Graph G, int s) {
        marked[s] = true;
        id[s] = count;
        for (int temp : G.adj(s))
            if (!marked[temp]) {
                dfs(G, temp);
            }
    }

    //判斷點v和w是否在一個連通分支中
    public boolean connected(int v, int w) {
        if (id[v] == id[w])
            return true;
        else
            return false;
    }

    public int id(int v) {
        return id[v];
    }

    public int count() {
        return count;
    }
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34

相關推薦

第四章圖演算法總結

該部落格原地址http://blog.csdn.net/ntt5667781/article/details/52743342 其實就是對書上的內容做了個總結 在開始各類圖演算法之前，先將圖的結構進行分類。  圖的表示，在實際實現過程中，有以下幾種基本的

資訊學奧賽一本通（C++版） 第三部分 資料結構 第四章 圖論演算法

 資訊學奧賽一本通（C++版） 第三部分 資料結構   第四章 圖論演算法 http://ybt.ssoier.cn:8088/ 第一節 圖的遍歷 //1341 【例題】一筆畫問題 //在想，是輸出尤拉路，還是歐拉回路 //從哪點開始遍歷， //點的資料範圍，邊的資料範圍

資料結構——第四章圖：01圖相關定義

1.圖的定義：圖是一種網狀資料結構，形式化定義如下：圖Graph = (V, R)，V = {x | x ∈ DataObject}，R = {VR}，VR = {<x, y> | P(x, y) ∧ (x, y ∈ V)}。集合DataObject中的所有元素具有相同的特性。V中的資料元素通常為

資料結構——第四章圖：03圖的遍歷

1.圖的遍歷：從圖中某個頂點出發遊歷圖，訪遍圖中其餘頂點，並且使圖中的每個頂點僅被訪問一次的過程。有兩種遍歷方式：深度優先遍歷、廣度優先遍歷。 2.深度優先搜尋遍歷圖： （1）連通圖的深度優先搜尋遍歷：從圖中某個頂點v0出發，訪問此頂點，然後依次從v0的各個未被訪問的鄰接點出發深度優先搜尋遍歷圖，直至圖中

資料結構——第四章圖：04最小生成樹

1.（連通網的）最小生成樹問題提出：假設要在n個城市之間建立通訊聯絡網，則連通n個城市只需要修建n-1條線路，如果在最節省經費的前提下建立這個通訊網？該問題等價於：構造網的一棵最小生成樹，即：在e條帶權的邊中選取n-1條邊（不構成迴路），使權值之和為最小。有兩種演算法：Prim（普利姆）演算法和Kruskal

資料結構——第四章圖：06求兩點之間的最短路徑

1.求兩點之間的最短路徑： （1）求從某個源點到其餘各點的最短路徑：Dijstra（迪傑斯特拉）演算法； （2）求每一對頂點之間的最短路徑：Floyd（弗洛伊德）演算法。 2.Dijstra演算法的基本思想：依據最短路徑的長度遞增的次序求得各條路徑。其中，從源點到頂點v的最短路徑是所有最短路徑中長度最短

第四章 資料庫安全性總結

一：資料庫安全性 1：問題的提出 1：資料庫的一大特點是資料可以共享 2：資料共享必然帶來資料庫的安全性問題 3：資料庫系統中的資料共享不能是無條件的共享 例： 軍事祕密、國家機密、新產品實驗資料、市場需求分析、市場營銷策略、銷售計劃、客戶檔案、醫療檔案、銀行儲蓄資料 &nb

c++ primer plus（第六版） 第四章重點內容總結 以及手碼練習題答案

1.陣列 可儲存多個同類型的的值。宣告時候 型別 陣列名【元素個數】。其中元素個數必須是整型常數或者const值，常量表達式。c++陣列都是從0開始編號。最後一個元素的索引比陣列長度小一。貌似編譯器不會檢查使用的下表是否有效。sizeof用於陣列名時得到整個陣列中的位元組數

大話資料結構讀書筆記艾提拉總結 查詢演算法 和排序演算法比較好 第1章資料結構緒論 1 第2章演算法 17 第3章線性表 41 第4章棧與佇列 87 第5章串 123 第6章樹 149 第7章圖 21

大話資料結構讀書筆記艾提拉總結   查詢演算法 和排序演算法比較好     第1章資料結構緒論 1 第2章演算法 17 第3章線性表 41 第4章棧與佇列 87 第5章串 123 第6章樹 149 第7章圖 211

讀完第四章《兩人合作》的內容後的總結

learn 處理 總結 str 放棄 價值 內容 驗證 我認 兩人合作是團隊合作的基礎；這裏介紹的這個基礎型“團隊”中通用的一些方法以及最重要的——交流——的細節 1.代碼規範 代碼風格規範。主要是文字上的規定； 縮進：4個空格，而不是tab； 關於斷行與空白的{}

第四章總結

程序 交換 幫助 格式 由於 編程 代碼 機器 更多 一、代碼規範 需要我們在編程中特別註意這一點，要保持代碼工整可修改，無二義性，每一行一句代碼盡量加以註釋。不僅是要讓機器編譯讀懂，還要程序員能讀懂 二、代碼風格、設計規範 在代碼設計規範中，要考慮程序設計、模塊之

第四章第五章 環境搭建和24個命令總結

gpl和gun 基本命令 cpGUN 和 GPL GUN‘s not Unix 遞歸寫法，簡寫也是GUN1. GUN 是84年自由軟件資金會牽頭弄的一個類unix操作系統，但是因為它不實用，而且總是跳票，所以並沒有流行起來。2. 但是它裏面的很多軟件是很好的，比如bash，這些都被用在了linux系統

.NET第四章總結

win 右鍵菜單 系統托盤 任務欄顯示 技術 問題 路徑 退出 form 　　　　　　　　　　　　　　　　　　　　　　　　　　.NET第四章簡單總結　　　　 1、簡單的獲取文件路徑： 2、回車跳轉控件焦點

《數學之美》讀書記錄【思維導圖記錄】：第四章，談談中文分詞

post IT .cn splay top style title mage blog 《數學之美》讀書記錄【思維導圖記錄】：第四章，談談中文分詞

【知識點總結】第四章 類與對象

分享 ima src 對象分配 height ted 公有 功能 簡化 面向對象程序設計的基本概念和特征 抽象性：對對象進行概括，抽出一類對象的公共性質並加以描述的過程。【數據抽象、行為抽象】 封裝性：將抽象得到的數據、行為、功能相結合，形成一個有機的整體。就是將數據與

Python之旅.第四章.模塊與包.總結（未完待遇）

standard 後綴 att 擔心 lse 綁定 做的 業務 搜索 一、模塊 模塊： 一系列功能的集合體，在python中一個py文件就是一個模塊，模塊名就是py文件的文件名； 模塊的好處： 1.減少重復的代碼 2.拿來主義 定義模塊： 就是創建一個py文件；

第四章：活動圖

分享圖片 只有一個 什麽 分叉 img 面向 png 對象流 有一個 活動圖明確先做什麽，後坐什麽，什麽條件下做什麽。 活動圖也可以不面向對象，但流程圖一定面向過程。 一個活動圖一定有只有一個初始節點。終點為1～n。 如果有多個終點那麽可以有描述。

Windows核心編程之核心總結（第四章 進程（一））（2018.6.8)

Windows核心編程之核心總結學習目標 第四章進程的學習可謂是任重而道遠，雖然不難，但知識量很多，也比較零散，需要多總結，腦海裏才有進程的框架。所以，我把本章分為幾個小節來講完。我還是一如既往的添加輔助性內容，希望對於小白有所幫助。而比我流弊的大有人在，大神們可以跳過輔助性內容。本小節的學習目標如下：1.C

Windows核心編程之核心總結（第四章 進程（二））（2018.6.17)

函數的參數 設置 函數詳解 可執行文件 一次 HA AC 關聯 原型 學習目標 上一節我們了解了進程、入口函數和進程實例句柄等內容，在進入進程的命令行學習前，有一個全局變量初始化問題需要測試一波。本節的學習目標如下：1.測試C/C++運行庫啟動函數初始化哪些全局變量2.進程

Windows核心編程之核心總結（第四章 進程（三））（2018.6.21)

擁有 mar eset cto 繼續 detached iat head opera 學習目標 本章節將學習以後經常用到的CreateProcess函數，聽網上的人說有些面試官喜歡問這個函數的大概功能和參數作用哦，可見這個函數是十分重要滴，那我們來詳細了解和測試這個函數的功