2. 程式人生 > >卷積操作和反捲積操作的數學解釋

卷積操作和反捲積操作的數學解釋

阿新 • • 發佈：2018-12-30

三個月沒更新了啊，回來更一發～～

csdn上主要講一些coding過程中遇到的函式，問題，解決方案。偏實踐

另外，如果你想看一些理論方面的東西，歡迎加我的知乎知乎主頁

csdn私信幾乎不看，有問題交流可以發郵箱：或者知乎私信，看到我會第一時間回覆各位

之前的文章裡有人和我提了引數位置的問題，非常感謝。之前我用的tensorflow版本是0.8，在1.0大改以後很多引數交換了位置，所以我更新了版本到1.1.0rc1，請大家看程式碼的時候注意一下版本問題

/*******************************************************************************************************************************************************/

今天來介紹一下Tensorflow裡面的反捲積操作，網上反捲積的用法的介紹比較少，希望這篇教程可以幫助到各位

首先無論你如何理解反捲積，請時刻記住一點，反捲積操作是卷積的反向

如果你隨時都記住上面強調的重點，那你基本就理解一大半了，接下來通過一些函式的介紹為大家強化這個觀念

conv2d_transpose(value, filter, output_shape, strides, padding="SAME", data_format="NHWC", name=None)
除去name引數用以指定該操作的name，與方法有關的一共六個引數：
第一個引數value：指需要做反捲積的輸入影象，它要求是一個Tensor

 
第二個引數filter：卷積核，它要求是一個Tensor，具有[filter_height, filter_width, out_channels, in_channels]這樣的shape，具體含義是[卷積核的高度，卷積核的寬度，卷積核個數，影象通道數]
第三個引數output_shape：反捲積操作輸出的shape，細心的同學會發現卷積操作是沒有這個引數的，那這個引數在這裡有什麼用呢？下面會解釋這個問題
第四個引數strides：反捲積時在影象每一維的步長，這是一個一維的向量，長度4
第五個引數padding：string型別的量，只能是"SAME","VALID"其中之一，這個值決定了不同的卷積方式

 
第六個引數data_format：string型別的量，'NHWC'和'NCHW'其中之一，這是tensorflow新版本中新加的引數，它說明了value引數的資料格式。'NHWC'指tensorflow標準的資料格式[batch, height, width, in_channels]，'NCHW'指Theano的資料格式,[batch, in_channels，height, width]，當然預設值是'NHWC'

開始之前務必瞭解卷積的過程，參考我的另一篇文章：http://blog.csdn.net/mao_xiao_feng/article/details/53444333
首先定義一個單通道圖和3個卷積核
[python] view plain copy print?
  1. x1 = tf.constant(1.0, shape=[1,3,3,1])  
  2. kernel = tf.constant(1.0, shape=[3,3,3,1])  
x1 = tf.constant(1.0, shape=[1,3,3,1])
kernel = tf.constant(1.0, shape=[3,3,3,1])


先彆著急！我們不直接用反捲積函式，而是再定義一些圖[python] view plain copy print?
  1. x2 = tf.constant(1.0, shape=[1,6,6,3])  
  2. x3 = tf.constant(1.0, shape=[1,5,5,3])  
x2 = tf.constant(1.0, shape=[1,6,6,3])
x3 = tf.constant(1.0, shape=[1,5,5,3])


x2是6×6的3通道圖，x3是5×5的3通道圖
好了，接下來對x3做一次卷積操作[python] view plain copy print?
  1. y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding=“SAME”)  
y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding="SAME")

所以返回的y2是一個單通道的圖，如果你瞭解卷積過程，很容易看出來y2是[1，3，3，1]的Tensor，y2的結果如下：[python] view plain copy print?
  1. [[[[ 12.]  
  2.    [ 18.]  
  3.    [ 12.]]  
  4.   [[ 18.]  
  5.    [ 27.]  
  6.    [ 18.]]  
  7.   [[ 12.]  
  8.    [ 18.]  
  9.    [ 12.]]]]  
[[[[ 12.]
   [ 18.]
   [ 12.]]

  [[ 18.]
   [ 27.]
   [ 18.]]

  [[ 12.]
   [ 18.]
   [ 12.]]]]

又一個很重要的部分！tf.nn.conv2d中的filter引數，是[filter_height, filter_width, in_channels, out_channels]的形式，而tf.nn.conv2d_transpose中的filter引數，是[filter_height, filter_width, out_channels，in_channels]的形式，注意in_channels和out_channels反過來了！因為兩者互為反向，所以輸入輸出要調換位置
既然y2是卷積操作的返回值，那我們當然可以對它做反捲積，反捲積操作返回的Tensor，應該和x3的shape是一樣的（不難理解，因為是卷積的反過程）[python] view plain copy print?
  1. y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3], strides=[1,2,2,1],padding=“SAME”)  
y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3], strides=[1,2,2,1],padding="SAME")


好，現在返回的y3果然是[1，5，5，3]的Tensor，結果如下：[python] view plain copy print?
  1. [[[[ 12.12.12.]  
  2.    [ 30.30.30.]  
  3.    [ 18.18.18.]  
  4.    [ 30.30.30.]  
  5.    [ 12.12.12.]]  
  6.   [[ 30.30.30.]  
  7.    [ 75.75.75.]  
  8.    [ 45.45.45.]  
  9.    [ 75.75.75.]  
  10.    [ 30.30.30.]]  
  11.   [[ 18.18.18.]  
  12.    [ 45.45.45.]  
  13.    [ 27.27.27.]  
  14.    [ 45.45.45.]  
  15.    [ 18.18.18.]]  
  16.   [[ 30.30.30.]  
  17.    [ 75.75.75.]  
  18.    [ 45.45.45.]  
  19.    [ 75.75.75.]  
  20.    [ 30.30.30.]]  
  21.   [[ 12.12.12.]  
  22.    [ 30.30.30.]  
  23.    [ 18.18.18.]  
  24.    [ 30.30.30.]  
  25.    [ 12.12.12.]]]]  
[[[[ 12.  12.  12.]
   [ 30.  30.  30.]
   [ 18.  18.  18.]
   [ 30.  30.  30.]
   [ 12.  12.  12.]]

  [[ 30.  30.  30.]
   [ 75.  75.  75.]
   [ 45.  45.  45.]
   [ 75.  75.  75.]
   [ 30.  30.  30.]]

  [[ 18.  18.  18.]
   [ 45.  45.  45.]
   [ 27.  27.  27.]
   [ 45.  45.  45.]
   [ 18.  18.  18.]]

  [[ 30.  30.  30.]
   [ 75.  75.  75.]
   [ 45.  45.  45.]
   [ 75.  75.  75.]
   [ 30.  30.  30.]]

  [[ 12.  12.  12.]
   [ 30.  30.  30.]
   [ 18.  18.  18.]
   [ 30.  30.  30.]
   [ 12.  12.  12.]]]]


這個結果是怎麼得來的？可以用一張動圖來說明,圖片來源：反捲積的真正含義

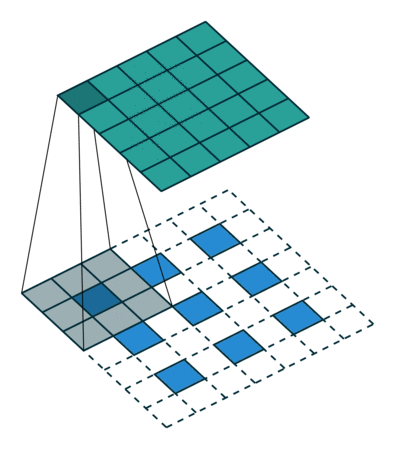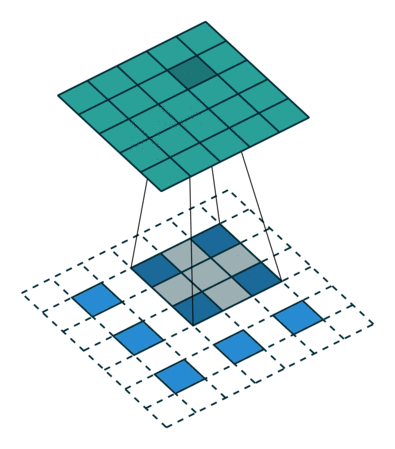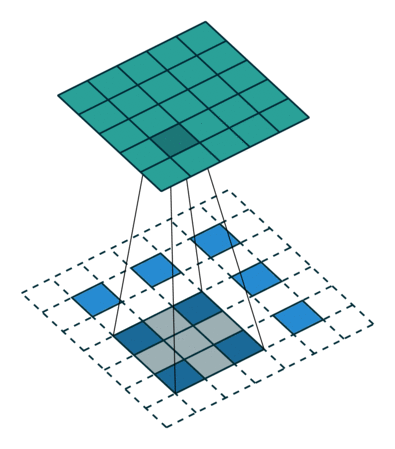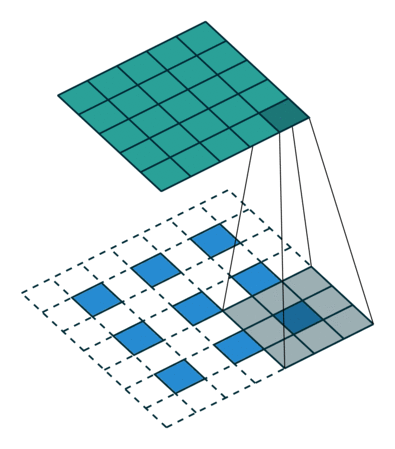
看起來，tf.nn.conv2d_transpose的output_shape似乎是多餘的，因為知道了原圖，卷積核，步長顯然是可以推出輸出影象大小的，那為什麼要指定output_shape呢？
看這樣一種情況：[python] view plain copy print?
  1. y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding=“SAME”)  
y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding="SAME")


我們把上面的x2也做卷積，獲得shape為[1，3，3，1]的y4如下：[python] view plain copy print?
  1. [[[[ 27.]  
  2.    [ 27.]  
  3.    [ 18.]]  
  4.   [[ 27.]  
  5.    [ 27.]  
  6.    [ 18.]]  
  7.   [[ 18.]  
  8.    [ 18.]  
  9.    [ 12.]]]]  
[[[[ 27.]
   [ 27.]
   [ 18.]]

  [[ 27.]
   [ 27.]
   [ 18.]]

  [[ 18.]
   [ 18.]
   [ 12.]]]]


[1，6，6，3]和[1，5，5，3]的圖經過卷積得到了相同的大小，[1，3，3，1]
讓我們再反過來看，那麼[1，3，3，1]的圖反捲積後得到什麼呢？產生了兩種情況。所以這裡指定output_shape是有意義的，當然隨意指定output_shape是不允許的，如下情況程式會報錯：[python] view plain copy print?
  1. y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],strides=[1,2,2,1],padding=“SAME”)  
y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],strides=[1,2,2,1],padding="SAME")
以上是stride為2的情況，為1時也類似，當卷積核大於原圖時，預設用VALID方式（用SAME就無意義了）參考下圖：


程式清單：
[python] view plain copy print?
  1. import tensorflow as tf  
  2. x1 = tf.constant(1.0, shape=[1,3,3,1])  
  3. x2 = tf.constant(1.0, shape=[1,6,6,3])  
  4. x3 = tf.constant(1.0, shape=[1,5,5,3])  
  5. kernel = tf.constant(1.0, shape=[3,3,3,1])  
  6. y1 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,6,6,3],  
  7.     strides=[1,2,2,1],padding=“SAME”)  
  8. y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding=“SAME”)  
  9. y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3],  
  10.     strides=[1,2,2,1],padding=“SAME”)  
  11. y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding=“SAME”)  
  12. ””’ 
  13. Wrong!!This is impossible 
  14. y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],strides=[1,2,2,1],padding=”SAME”) 
  15. ”’
  16. sess = tf.Session()  
  17. tf.global_variables_initializer().run(session=sess)  
  18. x1_decov, x3_cov, y2_decov, x2_cov=sess.run([y1,y2,y3,y4])  
  19. print(x1_decov.shape)  
  20. print(x3_cov.shape)  
  21. print(y2_decov.shape)  
  22. print(x2_cov.shape)  
import tensorflow as tf

x1 = tf.constant(1.0, shape=[1,3,3,1])

x2 = tf.constant(1.0, shape=[1,6,6,3])

x3 = tf.constant(1.0, shape=[1,5,5,3])

kernel = tf.constant(1.0, shape=[3,3,3,1])



y1 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,6,6,3],
    strides=[1,2,2,1],padding="SAME")

y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding="SAME")

y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3],
    strides=[1,2,2,1],padding="SAME")

y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding="SAME")

'''
Wrong!!This is impossible
y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],strides=[1,2,2,1],padding="SAME")
'''
sess = tf.Session()
tf.global_variables_initializer().run(session=sess)
x1_decov, x3_cov, y2_decov, x2_cov=sess.run([y1,y2,y3,y4])
print(x1_decov.shape)
print(x3_cov.shape)
print(y2_decov.shape)
print(x2_cov.shape)


                </div>

PS：
反捲積中需要注意多了一個output_shape引數，注意它的引數設定；
注意tf.nn.conv2d_transpose中的kernel如何設定[filter_size,filter_size,output_channel,input_channel]。

注意無論卷積或者非卷積運算在實現上豆採用兩個矩陣進行矩陣乘法運算，因此需要注意，在卷積的時候，我們採用怎樣的矩陣進行運算，轉化為對應的矩陣，注意反捲積（轉置卷積）的過程中，兩個矩陣代表的什麼東東？一個代表資料，一個代表卷積核中的資料，卷積為Y_=CX_,其中Y_和X_都為[x,1]的資料格式，Y_代表卷積後的資料，X_代表卷積前的資料！反捲積則為X_=C(T)Y_，其中C(T)是個拓普利茲矩陣，可以百度一下這個矩陣的定義哈！
參考：
【caffe】caffe之反捲積層

相關推薦

卷積操作和反捲積操作的數學解釋

三個月沒更新了啊，回來更一發～～ csdn上主要講一些coding過程中遇到的函式，問題，解決方案。偏實踐 另外，如果你想看一些理論方面的東西，歡迎加我的知乎知乎主頁 csdn私信幾乎不看，有問題交流可以發郵箱：[email protec

深度學習之卷積和反捲積tensorflow

ps 零零總總接觸深度學習有1年了，雖然時間是一段一段的。現在再拾起來做一個新的專案，有些東西又要重新理解，感覺麻煩。現在就再次學習時候有些困惑的地方捋一遍。 1.卷積 說到卷積，我現在還有印象的是大學裡《訊號與系統》和《數字訊號處理》兩書中的離散訊號的卷積。簡單來你說就是一個訊號固定，一個

神經網路中的卷積和反捲積原理

一.卷積 在深度學習的過程中，很多神經網路都會用到各種卷積核來進行操作，那麼我們就簡單講一下卷積的原理和實現過程。 那麼卷積在神經網路中的作用是什麼呢？一開始的傳統神經網路是沒有卷積層的，都是隱藏層加生全連線層的結構，這樣在中間得到的特徵都是線性的，不能提取到一個區域性的特徵。而卷積

輕鬆理解轉置卷積(transposed convolution)/反捲積(deconvolution)

原文地址:Up-sampling with Transposed Convolution 在CNN中,轉置卷積是一種上取樣(up-sampling)的方法.如果你對轉置卷積感到困惑,那麼就來讀讀這篇文章吧. 本文的notebook程式碼在Github. 上取樣的需要 在

tensorflow 卷積/反卷積-池化/反池化操作詳解

sha ted href ref 操作 int inpu ase 反卷積 Plese see this answer for a detailed example of how tf.nn.conv2d_backprop_input and tf.nn.conv2d_b

TensorFlow演示反捲積的操作

一 反捲積函式介紹1 語法格式def conv2d_transpose(value,filter,output_shape,strides,padding="SAME",data_format="NHWC",name=None):2 引數說明value：代表通過卷積操作之後的

卷積、反捲積、轉置卷積和微步幅卷積

卷積 首先定義本文要用到的符號 輸入圖片的大小: i1=i2=i。 卷積核的大小: k1=k2=k。 卷積步長:s1=s2=s。 填充padding=p。 下圖表示引數為(i=5,k=3,s=2,p=1)的卷積計算過程，可以看出輸出的圖片大小是(3∗3

空洞卷積與反捲積

空洞卷積（dilated conv），也稱擴張卷積。空洞卷積可以在kernel有效增大感受野的同時不增加模型引數或者計算量。在影象需要全域性資訊或者語音文字需要較長的sequence資訊依賴的問題中，都能較好的應用空洞卷積。在影象分割，語音合成WaveNet，機器翻譯ByteNet中都有

深度學習：卷積，反池化，反捲積，卷積可解釋性，CAM ,G_CAM

憑什麼相信你，我的CNN模型？（篇一：CAM和Grad-CAM)：https://www.jianshu.com/p/1d7b5c4ecb93 憑什麼相信你，我的CNN模型？（篇二：萬金油LIME)：http://bindog.github.io/blog/2018/02/11/model-ex

對深度可分離卷積、分組卷積、擴張卷積、轉置卷積（反捲積）的理解

轉自：https://blog.csdn.net/chaolei3/article/details/79374563   參考： https://zhuanlan.zhihu.com/p/28749411 https://zhuanlan.zhihu.com/p/28186

卷積與反捲積 步長（stride）與重疊（overlap）及 output 的大小

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

深度學習基礎--卷積--反捲積(deconvolution)

反捲積(deconvolution)   這個概念很混亂，沒有統一的定義，在不同的地方出現，意義卻不一樣。   上取樣的卷積層有很多名字： 全卷積（full convolution）， 網路內上取樣（ in-network upsampling）， 微步幅卷積（fractio

個人總結：關於tf.nn.conv2d（卷積）與tf.nn.conv2d_transpose（反捲積）的區別

官網中對於卷積tf.nn.conv2d的描述 tf.nn.conv2d(     input,     filter,     strides,     padding,     use_cudn

[CNN] 卷積、反捲積、池化、反池化

之前一直太忙，沒時間整理，這兩天抽出點時間整理一下卷積、反捲積、池化、反池化的內容，也希望自己對一些比較模糊的地方可以理解的更加清晰。 一、卷積 1、卷積的簡單定義 卷積神經網路中的卷積操作可以看做是輸入和卷積核的內積運算。其運算過程非常容易理解，下面有舉例。 2、舉例解

深度學習中反捲積層(轉置卷積)引起的棋盤格噪聲

在基於CNN的超解析度中，經常在最後一層使用stride>1的deconv layer，而這會造成棋盤格噪聲。如下圖所示   具體產生原因 上面的黑格子是表示原始影象中的某一個畫素點，白色的表示轉置卷積中的stride，一般是用0去填充。下面一層就是deconv生成的影象。可以看到s

轉置卷積(反捲積)

借鑑於此個部落格，寫的非常好：https://blog.csdn.net/isMarvellous/article/details/80087705 轉置卷積（Transposed Convolution）也叫做反捲積（Deconvolution） Pytorch中可以使用torch.nn.

卷積神經網路CNN（1）——影象卷積與反捲積（後卷積，轉置卷積）

1.前言    傳統的CNN網路只能給出影象的LABLE，但是在很多情況下需要對識別的物體進行分割實現end to end，然後FCN出現了，給物體分割提供了一個非常重要的解決思路，其核心就是卷積與反捲積，所以這裡就詳細解釋卷積與反捲積。     對於1維的卷積，公式（離散

深度學習中的卷積與反捲積

卷積與反捲積操作在影象分類、影象分割、影象生成、邊緣檢測等領域都有很重要的作用。為了講明白這兩種操作，特別是反捲積操作，本文將依照神經網路中的編碼器——>解碼器——>卷積——>反捲積 的思路來一步步介紹。 編碼器與解碼器 神經網路本質

反捲積 逆卷積 轉置卷積(Transposed Convolution；Fractionally Strided Convolution；Deconvolution) 輸出維度shape計算

正常卷積運算： 如上圖：4x4的輸入，卷積Kernel為3x3, ,輸出為2x2。其計算可以理解為： 輸入矩陣展開為4*4=16維向量，記作x 輸出矩陣展開為2*2=4維向量，記作y 卷積核C為如下矩陣： 卷積運算可表示為y = Cx（可以對照

深度學習---影象卷積與反捲積（最完美的解釋）

動態圖1.前言   傳統的CNN網路只能給出影象的LABLE，但是在很多情況下需要對識別的物體進行分割實現end to end，然後FCN出現了，給物體分割提供了一個非常重要的解決思路，其核心就是卷積與反捲積，所以這裡就詳細解釋卷積與反捲積。    對於1維的卷積，公式（離散