● 每週一言

動嘴，動腦，都不如動手去做。

導語

在分析樣本資料情況時，都需要看一看方差。在概率統計學中，方差是衡量資料離散程度的一種度量，樣本的方差越大，樣本間的偏離程度就越大，反之越小。而在資料量巨大或者較難獲得總體樣本時，按照方差標準公式計算出來的實際方差，通常並非樣本的真實方差。

因此，為了保證無偏計算，大資料量下用取樣資料計算方差時，是除以n-1而不是n。那麼，為什麼除以n-1就能保證計算出來的方差是真實方差？

方差

在詳細推導過程前，我們先明確以下幾個數學符號的概念。n表示可採樣的樣本數量，xi表示樣本資料，x拔表示樣本均值，μ表示樣本的真實均值，S平方表示樣本實際方差，σ平方

根據方差的標準計算公式，有如下推導：

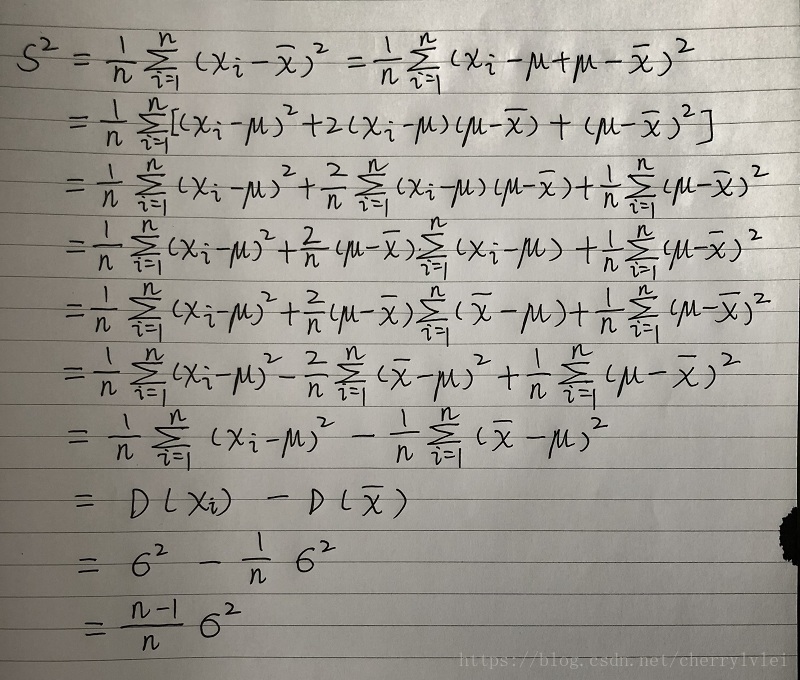
上式第一個比較關鍵的變換是第四行到第五行。由於第四行中間式子的後半段是樣本資料累加，因此可以把xi替換成x拔，使累加結果不改變。

此外，由於μ和x拔在既定樣本集上是固定的，第三行到第四行和第五行到第六行的推導，可以這樣把 (μ - x拔) 先提出來又放進累加操作。

第二個比較關鍵的變換是平均數x拔的方差，是樣本方差的n分之一。這個可以利用方差變換公式來推導，如下：

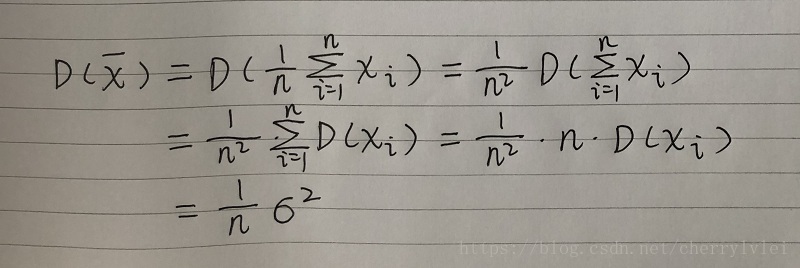
這裡解釋一下為什麼每一個樣本xi的方差，都等於樣本的總體方差。

樣本xi代表所有可能出現的情況，每一個x1、x2、x3…都分別可以看作是一個隨機變數，而這些隨機變數之間沒有差別，其分佈也跟樣本總體分佈相同，所以它們的方差自然也是相同的。

上面的推導是針對一維資料的方差推導，當然，推廣到多維資料也是同樣適用的。

這裡順便介紹一下多維資料的方差，多維資料的方差稱為 協方差。協方差是衡量樣本資料不同維度之間變化關係的度量，具體計算公式如下：

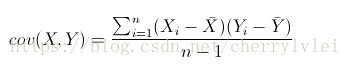
雖然叫協方差，但是意義和方差不同。協方差大於0表示X和Y正相關，小於0則表示負相關，等於0則不相關，值越大或越小表示它們的相關程度越高。協方差還能得出皮爾森相關係數的計算公式。

在多維資料情況下，通常使用協方差矩陣來表示不同維度之間的協方差。

以上便是方差的講解，敬請期待下節內容。

結語

感謝各位的耐心閱讀，後續文章於每週日奉上，敬請期待。歡迎大家關注小鬥公眾號 對半獨白！