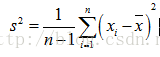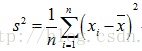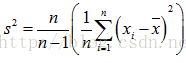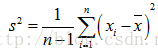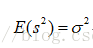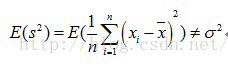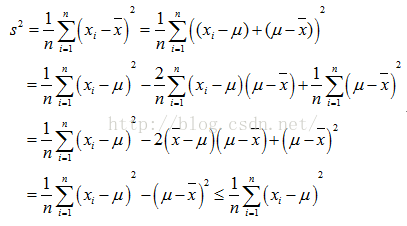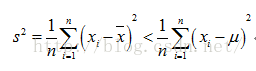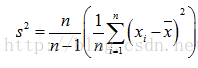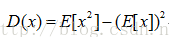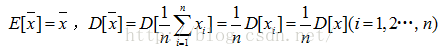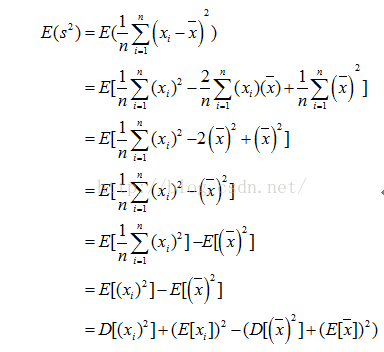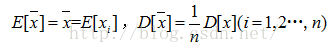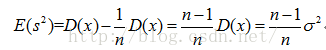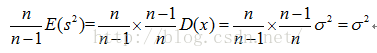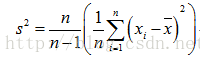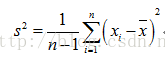前段日子重新整理了一下這個問題的解答，跟大家分享一下，如果有什麼錯誤的話希望大家能夠提出來，我會及時改正的，話不多說進入正題：

首先，我們來看一下樣本方差的計算公式：

剛開始接觸這個公式的話可能會有一個疑問就是：為什麼樣本方差要除以（n-1）而不是除以n？為了解決這個疑惑，我們需要具備一點統計學的知識基礎，關於總體、樣本、期望（均值）、方差的定義以及統計估計量的評選標準。有了這些知識基礎之後，我們會知道樣本方差之所以要除以（n-1）是因為這樣的方差估計量才是關於總體方差的無偏估計量。這個公式是通過修正下面的方差計算公式而來的：

修正過程為：

                             
我們看到的其實是修正後的結果：

   對於這種修正的話是有相關的公式推導的。下面都會一一給出。

為了方便敘述，在這裡說明好數學符號：

前面說過樣本方差之所以要除以（n-1）是因為這樣的方差估計量才是關於總體方差的無偏估計量。在公式上來講的話就是樣本方差的估計量的期望要等於總體方差。如下：

但是沒有修正的方差公式，它的期望是不等於總體方差的

也就是說，樣本方差估計量如果是用沒有修正的方差公式來估計總計方差的話是有偏差的

下面給出比較好理解的公式推導過程：

也就是說，除非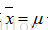否則一定會有

需要注意的是不等式右邊的才是的對方差的“正確”估計，但是我們是不知道真正的總體均值是多少的，只能通過樣本的均值來代替總體的均值。所以樣本方差估計量如果是用沒有修正的方差公式來估計總計方差的話是會有偏差，是會低估了總體的樣本方差的。為了能無偏差的估計總體方差，所以要對方差計算公式進行修正，修正公式如下：

                     
   這種修正後的估計量將是總體方差的無偏估計量，下面將會給出這種修正的一個來源；

為了能搞懂這種修正是怎麼來的，首先我們得有下面幾個等式：

1.方差計算公式：  

2. 均值的均值、方差計算公式：

對於沒有修正的方差計算公式我們有： 

因為：

所以有：

在這裡如果想修正的方差公式，讓修正後的方差公式求出的方差的期望為總體方差的話就需要在沒有修正的方差公式前面加上來進行修正，即：

                  
所以就會有這樣的修正公式：

而我們看到的都是修正後的最終結果：

這就解釋了為什麼要對方差計算公式進行修正，且為什麼要這樣修正。

上面的解釋如果有什麼錯誤，或者有哪些解釋不正確的地方歡迎大家指正。謝謝大家。希望能對大家有點幫助。