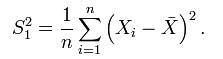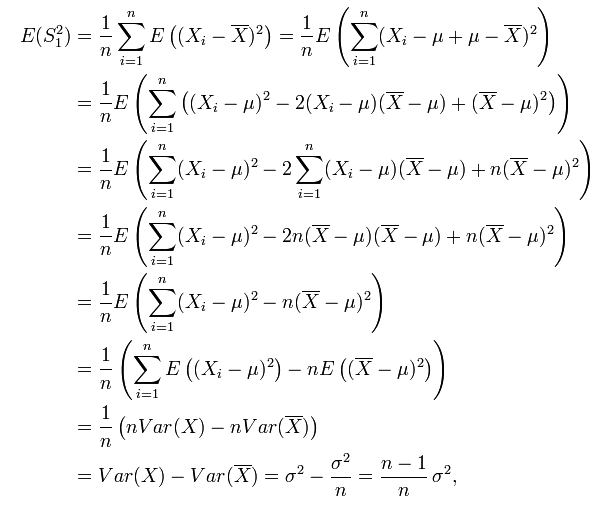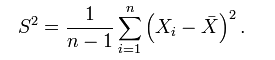為什麼樣本方差(sample variance)的分母是 n-1?
阿新 • • 發佈:2019-01-05
樣本方差計算公式裡分母為 的目的是為了讓方差的估計是無偏的。無偏的估計(unbiased
estimator)比有偏估計(biased estimator)更好是符合直覺的,儘管有的統計學家認為讓mean square error即MSE最小才更有意義,這個問題我們不在這裡探討;不符合直覺的是,為什麼分母必須得是
的目的是為了讓方差的估計是無偏的。無偏的估計(unbiased
estimator)比有偏估計(biased estimator)更好是符合直覺的,儘管有的統計學家認為讓mean square error即MSE最小才更有意義,這個問題我們不在這裡探討;不符合直覺的是,為什麼分母必須得是 而不是
而不是 才能使得該估計無偏。我相信這是題主真正困惑的地方。
才能使得該估計無偏。我相信這是題主真正困惑的地方。
要回答這個問題,偷懶的辦法是讓困惑的題主去看下面這個等式的數學證明:
![\mathbb{E}\Big[\frac{1}{n-1} \sum_{i=1}^n\Big(X_i -\bar{X}\Big)^2 \Big]=\sigma^2](http://zhihu.com/equation?tex=%5Cmathbb%7BE%7D%5CBig%5B%5Cfrac%7B1%7D%7Bn-1%7D+%5Csum_%7Bi%3D1%7D%5En%5CBig%28X_i+-%5Cbar%7BX%7D%5CBig%29%5E2+%5CBig%5D%3D%5Csigma%5E2) .
.
但是這個答案顯然不夠直觀(教材裡面統計學家像變魔法似的不知怎麼就得到了上面這個等式)。
下面我將提供一個略微更友善一點的解釋。
==================================================================
===================== 答案的分割線 ===================================
==================================================================
首先,我們假定隨機變數 的數學期望
的數學期望 是已知的,然而方差
是已知的,然而方差 未知。在這個條件下,根據方差的定義我們有
未知。在這個條件下,根據方差的定義我們有
![\mathbb{E}\Big[\big(X_i -\mu\big)^2 \Big]=\sigma^2, \quad\forall i=1,\ldots,n,](http://zhihu.com/equation?tex=%5Cmathbb%7BE%7D%5CBig%5B%5Cbig%28X_i+-%5Cmu%5Cbig%29%5E2+%5CBig%5D%3D%5Csigma%5E2%2C+%5Cquad%5Cforall+i%3D1%2C%5Cldots%2Cn%2C)
由此可得
![\mathbb{E}\Big[\frac{1}{n} \sum_{i=1}^n\Big(X_i -\mu\Big)^2 \Big]=\sigma^2](http://zhihu.com/equation?tex=%5Cmathbb%7BE%7D%5CBig%5B%5Cfrac%7B1%7D%7Bn%7D+%5Csum_%7Bi%3D1%7D%5En%5CBig%28X_i+-%5Cmu%5CBig%29%5E2+%5CBig%5D%3D%5Csigma%5E2) .
.
因此 是方差
是方差 的一個無偏估計,注意式中的分母不偏不倚正好是
的一個無偏估計,注意式中的分母不偏不倚正好是 !
!
這個結果符合直覺,並且在數學上也是顯而易見的。
現在,我們考慮隨機變數 的數學期望
的數學期望 是未知的情形。這時,我們會傾向於無腦直接用樣本均值
是未知的情形。這時,我們會傾向於無腦直接用樣本均值 替換掉上面式子中的
替換掉上面式子中的 。這樣做有什麼後果呢?後果就是,
。這樣做有什麼後果呢?後果就是,
如果直接使用
這是因為:
![\begin{eqnarray}\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2 &=&\frac{1}{n}\sum_{i=1}^n\Big[(X_i-\mu) + (\mu -\bar{X}) \Big]^2\\&=&\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2 +\frac{2}{n}\sum_{i=1}^n(X_i-\mu)(\mu -\bar{X})+\frac{1}{n}\sum_{i=1}^n(\mu -\bar{X})^2 \\&=&\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2 +2(\bar{X}-\mu)(\mu -\bar{X})+(\mu -\bar{X})^2 \\&=&\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2 -(\mu -\bar{X})^2 \end{eqnarray}](http://zhihu.com/equation?tex=%5Cbegin%7Beqnarray%7D%0A%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cbar%7BX%7D%29%5E2+%26%3D%26%0A%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%5CBig%5B%28X_i-%5Cmu%29+%2B+%28%5Cmu+-%5Cbar%7BX%7D%29+%5CBig%5D%5E2%5C%5C%0A%26%3D%26%0A%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cmu%29%5E2+%0A%2B%5Cfrac%7B2%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cmu%29%28%5Cmu+-%5Cbar%7BX%7D%29%0A%2B%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28%5Cmu+-%5Cbar%7BX%7D%29%5E2+%5C%5C%0A%26%3D%26%0A%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cmu%29%5E2+%0A%2B2%28%5Cbar%7BX%7D-%5Cmu%29%28%5Cmu+-%5Cbar%7BX%7D%29%0A%2B%28%5Cmu+-%5Cbar%7BX%7D%29%5E2+%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cmu%29%5E2+%0A-%28%5Cmu+-%5Cbar%7BX%7D%29%5E2+%0A%5Cend%7Beqnarray%7D)
換言之,除非正好 ,否則我們一定有
,否則我們一定有
 ,
,
而不等式右邊的那位才是的對方差的“正確”估計!
這個不等式說明了,為什麼直接使用 會導致對方差的低估。
會導致對方差的低估。
那麼,在不知道隨機變數真實數學期望的前提下,如何“正確”的估計方差呢?答案是把上式中的分母 換成
換成 ,通過這種方法把原來的偏小的估計“放大”一點點,我們就能獲得對方差的正確估計了:
,通過這種方法把原來的偏小的估計“放大”一點點,我們就能獲得對方差的正確估計了:
![\mathbb{E}\Big[\frac{1}{n-1} \sum_{i=1}^n\Big(X_i -\bar{X}\Big)^2\Big]=\mathbb{E}\Big[\frac{1}{n} \sum_{i=1}^n\Big(X_i -\mu\Big)^2 \Big]=\sigma^2.](http://zhihu.com/equation?tex=%5Cmathbb%7BE%7D%5CBig%5B%5Cfrac%7B1%7D%7Bn-1%7D+%5Csum_%7Bi%3D1%7D%5En%5CBig%28X_i+-%5Cbar%7BX%7D%5CBig%29%5E2%5CBig%5D%3D%5Cmathbb%7BE%7D%5CBig%5B%5Cfrac%7B1%7D%7Bn%7D+%5Csum_%7Bi%3D1%7D%5En%5CBig%28X_i+-%5Cmu%5CBig%29%5E2+%5CBig%5D%3D%5Csigma%5E2.)
要回答這個問題,偷懶的辦法是讓困惑的題主去看下面這個等式的數學證明:
但是這個答案顯然不夠直觀(教材裡面統計學家像變魔法似的不知怎麼就得到了上面這個等式)。
下面我將提供一個略微更友善一點的解釋。
==================================================================
===================== 答案的分割線 ===================================
==================================================================
首先,我們假定隨機變數
由此可得
因此
這個結果符合直覺,並且在數學上也是顯而易見的。
現在,我們考慮隨機變數
如果直接使用
這是因為:
換言之,除非正好
而不等式右邊的那位才是的對方差的“正確”估計!
這個不等式說明了,為什麼直接使用
那麼,在不知道隨機變數真實數學期望的前提下,如何“正確”的估計方差呢?答案是把上式中的分母
至於為什麼分母是而不是
或者別的什麼數,最好還是去看真正的數學證明,因為數學證明的根本目的就是告訴人們“為什麼”;暫時我沒有辦法給出更“初等”的解釋了。
下面是另一個人的證明推導:
本來,按照定義,方差的
estimator 應該是這個:
但,這個
estimator 有 bias,因為:
而 (n-1)/n * σ² != σ²
,所以,為了避免使用有 bias 的 estimator,我們通常使用它的修正值 S²: