Catalan number，卡特蘭數又稱卡塔蘭數，是組合數學中一個常出現在各種計數問題中出現的數列。以比利時的數學家歐仁·查理·卡塔蘭 (1814–1894)命名。

卡特蘭數的前幾個數
前20項為（OEIS中的數列A000108）：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190

在這裡我只詳細證明一個例子：
(和我後面要寫的一個HD題目有關).(HD1133題)
即排隊買票問題(出棧次序問題)：
一個棧(無窮大)的進棧序列為1,2,3,..n,有多少個不同的出棧序列?
　　有2n個人排成一行進入公園。入場費1元。其中只有n個人有一張1元鈔票，另外n人只有2元鈔票，劇院無其它鈔票，問有多少中方法使得只要有2元的人買票，售票處就有1元的鈔票找零？(將持1元者到達視作將1元入棧，持2元者到達視作使棧中某1元出棧)

不難看出，該題求的是左端點為首元素的任意區間內，1的個數大於等於2的個數。

方法一：折現法
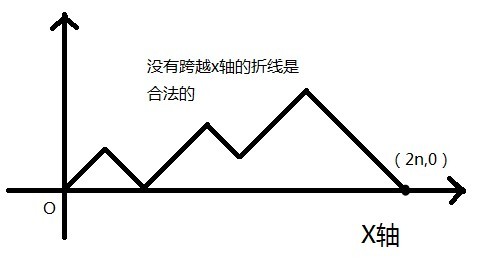
可以認為問題是，任意兩種操作，持1元者買票是操作一，持2元買票者是操作二。要求每種操作的總次數一樣，且進行第k次操作2前必須先進行至少k次操作1。我們假設一個人在原點，操作1是此人沿右上角45°走一個單位（一個單位設為根號2，這樣他第一次進行操作1就剛好走到（1,1）點），操作2是此人沿右下角45°走一個單位。第k次操作2前必須先進行至少k次操作1，就是說明所走出來的折線不能跨越x軸走到y=-1這條線上！在進行n次操作1和n此操作2後，此人必將到到達（2n，0）！若無跨越x軸的限制，折線的種數將為C（2n，n），即在2n次操作中選出n次作為操作1的方法數。

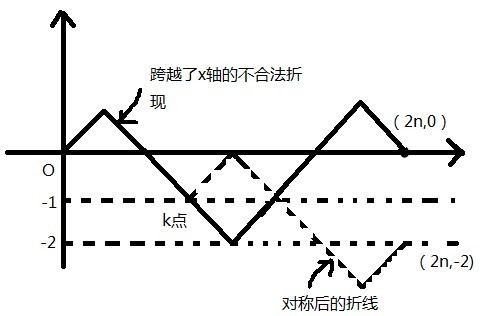
現在只要減去跨越了x軸的情況數。對於任意跨越x軸的情況，必有將與y=-1相交。找出第一個與y=-1相交的點k，將k點以右的折線根據y=-1對稱（即操作1與操作2互換了）。可以發現終點最終都會從（2n，0）對稱到（2n，-2）。由於對稱總是能進行的，且是可逆的。我們可以得出所有跨越了x軸的折線總數是與從（0,0）到（2n,-2）的折線總數。而後者的操作2比操作1要多0-（-2）=2次。即操作1為n-1,操作2為n+1。總數為C（2n，n-1）。

這個證明的關鍵就是最終一定會到達（2n,0)這個點。

對於不滿足情況的方案，它一定會越過y=-1，捉住這個特點，我們可將求不合法的方案數這個問題換個說法來：從（0，0）到（2n,-2)一共有多少種走法？這個走法數就是C(2n,n-1)因為走右下角的要多走2步，同時一共只走2n步，那就右下角走n+1步，方案法就是2n選n-1.

合法數=C(2n,n)-C(2n,n-1);

方法二：

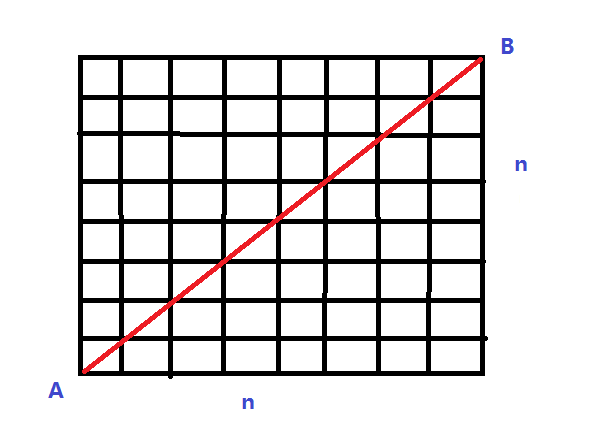
還可以等價為求從A點到B點不超過(可接觸)紅色對角線的最短路徑的數量。

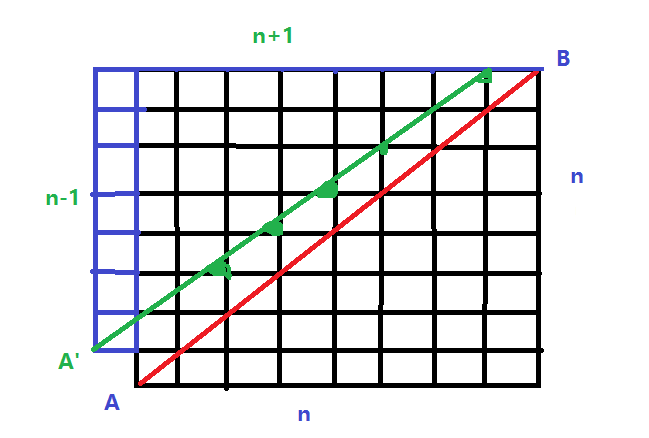
如圖，易知所有超過紅色紅色對角先的路徑都會碰到綠線。
對A做關於綠線的對稱點A’。則A’到B點的路徑總數即為非法路徑總數。

合法路徑數=總路徑數-非法路徑數=C(2n,n)-C(2n,n-1)。

每個人都是不一樣的，所以需要全排列* n!*n!

可以推廣到一般形式，1元的m人，2元的n人。
( C(m+n,n) - C(m+n,m+1) ) * m! * n!=
( C(m+n,n) - C(m+n,n-1) ) * m! * n!