BZOJ.4453.cys就是要拿英魂!(字尾陣列 單調棧 二分)
求字典序最大,容易想到對原串建字尾陣列求\(rk\)。
假設當前區間是\([l,r]\),對於在\([l,r]\)中的兩個字尾\(i,j\)(\(i<j\)),顯然我們不能直接比較\(rk_i,rk_j\)來比較\(i,j\)在\([l,r]\)中誰的字典序更大。(比如對於串\(babb\),\(l=1,r=3\),在原串中,字尾\(3(bb)\)的排名比\(1(babb)\)靠後,但是在\([1,3]\)中顯然應該是\(1\)的字典序更大)
但還是可以討論一下:
- 若\(rk_i>rk_j\),\(i\)在\([l,r]\)中的字典序一定比\(j\)大。
- 若\(rk_i<rk_j\),且\(LCP(i,j)<r-j+1\),\(j\)在\([l,r]\)中的字典序一定比\(i\)大。
- 若\(rk_i<rk_j\),且\(LCP(i,j)\geq r-j+1\),\(i\)在\([l,r]\)中的字典序一定比\(j\)大。
所以可以得到,對於\(i\),令\(j\)是\(i\)後邊第一個\(rk_j>rk_i\)的位置,\(i\)會在\([i,j+LCP(i,j)-1]\)這個區間成為答案(用\(R[i]\)表示\(i\)做答案的這個區間的右端點)。
所以我們把詢問按左端點排序,\(i\)從\(n\)到\(1\)倒著列舉,用單調棧維護這些可能成為答案的區間。
當列舉到\(i\)
我們每插入一個\(i\),它可能會覆蓋掉後面幾個區間成為最優解,如圖:
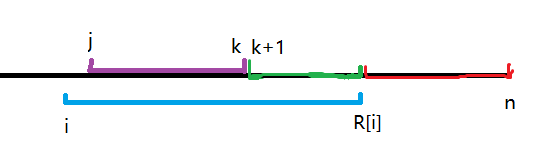
(此時單調棧中自底向上依次存的是紅色、綠色、紫色區間)
拿紫色的線段為例(假設紫色線段是由\(j\)作為答案,\(k\)就是\(R[j]\)),此時無論詢問右端點在點\(j\)還是在點\(k\),字尾\(i\)都要比\(j\)更優(字典序更大,比較方式同前文所說),所以藍色會覆蓋紫色,直接把紫色線段彈出棧。同理判斷藍色完全覆蓋綠色後也把綠色線段彈出棧。
然後在棧中加入元素:\(\{i,R[i],i\}\)
當然還會有這種情況:
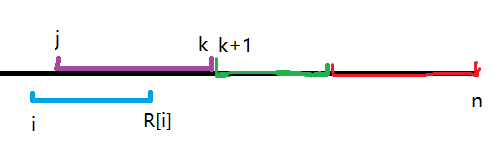
藍色\(i\)在紫色\(j\)的某左半段區間中會作為答案。
也就是當右端點在點\(j\)處時,\(i\)比\(j\)更優;而右端點在點\(k\)時,還是\(j\)比\(i\)更優。
此時我們可以二分找到\(R[i]\)。就是判斷右端點在哪個位置時,恰好使得字尾\(j\)比\(i\)更優。記這個位置為\(p\)。然後我們把\(j\)影響的區間\([j,k]\)改為\([p,k]\)。
此時\(i\)所影響的區間就是\([i,p-1]\)(\(R[i]=p-1\)),所以在棧中加入元素\(\{i,p-1,i\}\)。
(\(x\)影響區間\([l,r]\)就是指詢問右端點在\([l,r]\)中時\(x\)作為答案)
對於詢問\([l,r]\),此時\(l=i\),而單調棧中的區間是有序的。所以在單調棧中二分\(r\)在哪段區間中就可以了。
複雜度\(O((n+q)\log n)\)。
//12640kb 1076ms
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define gc() getchar()
typedef long long LL;
const int N=1e5+5;
struct Node
{
int l,r,p;
}sk[N];
struct Quries
{
int id,l,r;
inline bool operator <(const Quries &x)const
{
return l<x.l;
}
}q[N];
struct Suffix_Array
{
int tm[N],rk[N],sa[N],sa2[N],ht[N],Log[N],st[N][17];
char s[N];
inline void Init_ST(const int n)
{
for(int i=2; i<=n; ++i) Log[i]=Log[i>>1]+1;
for(int i=1; i<=n; ++i) st[i][0]=ht[i];
for(int j=1; j<=Log[n]; ++j)
for(int t=1<<j-1,i=n-t; i; --i)
st[i][j]=std::min(st[i][j-1],st[i+t][j-1]);
}
inline int LCP(int l,int r)
{
l=rk[l], r=rk[r]; if(l>r) std::swap(l,r);
++l;
int k=Log[r-l+1];
return std::min(st[l][k],st[r-(1<<k)+1][k]);
}
int Build()
{
scanf("%s",s+1);
const int n=strlen(s+1);
int *x=rk,*y=sa2,m=300;
for(int i=0; i<=m; ++i) tm[i]=0;
for(int i=1; i<=n; ++i) ++tm[x[i]=s[i]];
for(int i=1; i<=m; ++i) tm[i]+=tm[i-1];
for(int i=n; i; --i) sa[tm[x[i]]--]=i;
for(int k=1,p=0; k<n; k<<=1,m=p,p=0)
{
for(int i=n-k+1; i<=n; ++i) y[++p]=i;
for(int i=1; i<=n; ++i) if(sa[i]>k) y[++p]=sa[i]-k;
for(int i=0; i<=m; ++i) tm[i]=0;
for(int i=1; i<=n; ++i) ++tm[x[i]];
for(int i=1; i<=m; ++i) tm[i]+=tm[i-1];
for(int i=n; i; --i) sa[tm[x[y[i]]]--]=y[i];
std::swap(x,y), x[sa[1]]=p=1;
for(int i=2; i<=n; ++i)
x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?p:++p;
if(p>=n) break;
}
for(int i=1; i<=n; ++i) rk[sa[i]]=i;
ht[1]=0;
for(int i=1,k=0,p; i<=n; ++i)
{
if(rk[i]==1) continue;
if(k) --k;
p=sa[rk[i]-1];
while(i+k<=n && p+k<=n && s[i+k]==s[p+k]) ++k;
ht[rk[i]]=k;
}
Init_ST(n);
return n;
}
}sa;
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline bool Check(int i,int j,int r)
{
return sa.rk[i]>sa.rk[j]||sa.LCP(i,j)>=r-j+1;
}
int main()
{
static int Ans[N];
const int n=sa.Build(),Q=read();
for(int i=1; i<=Q; ++i) q[i]=(Quries){i,read(),read()};
std::sort(q+1,q+1+Q); q[0].l=0, sk[0].l=n+1;
int top=1,now=Q; sk[1]=(Node){n,n,n};
while(q[now].l==n) Ans[q[now--].id]=n;
for(int i=n-1; i; --i)
{
bool f=0;
while(top)
{
if(Check(i,sk[top].p,sk[top].r)) --top;
else if(Check(i,sk[top].p,sk[top].l)) {f=1; break;}
else break;
}
if(f)
{
int j=sk[top].p,l=sk[top].l,r=sk[top].r,mid;
while(l<r)
{
if(Check(i,j,mid=l+r>>1)) l=mid+1;
else r=mid;
}
sk[top].l=l;
}
sk[++top]=(Node){i,sk[top-1].l-1,i};
while(q[now].l==i)
{
int p=q[now].r,l=1,r=top,mid;
while(l<=r)
{
mid=l+r>>1;
if(p>=sk[mid].l && p<=sk[mid].r) break;
else if(p>sk[mid].r) r=mid-1;
else l=mid+1;
}
Ans[q[now--].id]=sk[mid].p;
}
}
for(int i=1; i<=Q; printf("%d\n",Ans[i++]));
return 0;
}