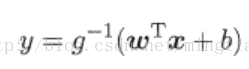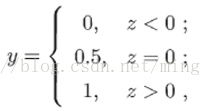邏輯迴歸模型(logistic regression)
邏輯迴歸模型意義
邏輯迴歸是機器學習中做分類任務常用的方法,屬於“廣義的線性模型”,即:
考慮二分類任務,其輸出標記y∈{0,1},而線性迴歸模型產生的預測值 z = wx+b是實值,於是,需要將實值z轉換為0/1值。最理想的是“單位階躍函式”:
即若預測值z大於0就判斷為正例,小於零則判斷為反例,預測值為臨界值零則可任意判斷。但是階躍函式不是連續的,不能直接作用於g-(),因此考慮用另一函式代替階躍函式,即sigmoid函式:
對應的影象:
可以看到sigmoid有如下特性(y = g(z),z=wx + b),當z>>0時,y->1,當z<<0時,y->0。這其實有著很強的實際意義(y就代表了該樣本屬於正例的概率),通過下張圖更好理解:
這是一個有著二維屬性的樣本分類任務(圖中h即上文y,w對應θ1、θ2,b用θ0替代),通過訓練樣本模型找到最好的[θ0,θ1,θ2](對應代價函式的極值點),而(θ0+θ1x1+θx2 =0)就對應著圖中的決策決策邊界(decision boundry)
對於測試樣本(x1,x2)來說,如果:
θ0+θ1x1+θ2x2(即z)>>0,說明其處於邊界線上方,距離邊界很遠,是一個正例概率很大,因此y = sigmoid(z)->1
θ0+θ1x1+θ2x2(即z)<<0,說明其處於邊界線下方,距離邊界很遠,它基本不可能是正例子,因此y = sigmoid(z)->0
θ0+θ1x1+θ2x2(即z)->0,說明其處於邊界線附近,是不是正例模稜兩可,因此y = sigmoid(z)->0.5(概率0.5)
邏輯迴歸模型求解引數(尋找θ)
邏輯迴歸的求解引數方式和一般優化問題沒有什麼不同,最基本的方式就是梯度下降法,只要寫出其代價函式以及引數θ的梯度公式即可(推導過程可參見其它教材):
值得注意的是邏輯迴歸的梯度更新公式與線性迴歸很像,但其實是有差別的,即hθ(x)的形式不同(邏輯迴歸為sigmoid函式):