紅黑樹的基本概念及java實現
紅黑樹的性質
紅黑樹和平衡二叉樹類似,最大的區別是紅黑樹為節點賦予了黑色和紅色兩種屬性。
- 紅黑樹的節點只有兩種顏色,紅色和黑色。
- 根節點為黑色。
- 葉子節點為黑色,值為NULL。
- 沒有兩個連續的紅色節點。
- 從一個節點到該節點的子孫節點的所有路徑包含相同數目的黑色節點。
平衡樹的旋轉
紅黑樹和AVL樹的平衡條件類似,當插入節點之後,可能會導致樹的某節點左右子樹高度差大於1。這時候我們需要左旋轉或者右旋轉來實現平衡的維持。
1、左旋:

2、右旋:
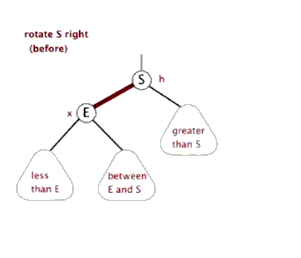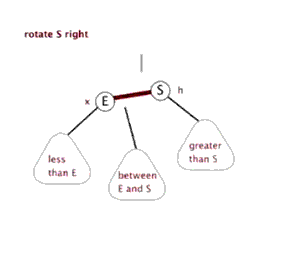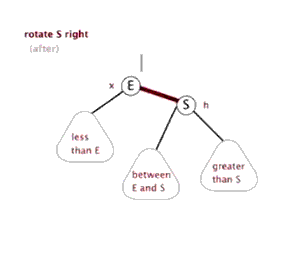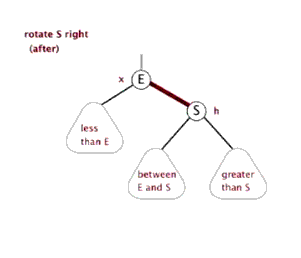
旋轉後我們可以發現有節點交換了連線位置,在左旋中,右側最小的節點轉換到了左側的最大處;在右旋中,左側的最大節點轉換到了右側的最小處。在旋轉前後依然滿足平衡樹的條件。
紅黑樹的基本操作
在對紅黑樹做插入、刪除,或是旋轉等操作時,紅黑樹的五條性質都需要滿足,我們不僅需要在適當的時候做一些旋轉,還需要對節點的顏色做一些適當的修改和調整。下面我們先來看看插入操作,假設插入的節點為紅色,插入分為幾種情況:
- 如果當前沒有節點,那麼插入的節點是根節點,直接塗上黑色。
- 如果插入的節點是其雙親節點的左子樹,若雙親節點和叔叔節點都是黑色,那麼可以直接插入,不用調整。
- 如果插入的節點是其雙親節點的左子樹,但雙親節點和叔叔節點都是紅色,那麼要把雙親節點和叔叔節點都塗黑,然後繼續向上調整顏色,直到滿足性質四。
- 如果插入的節點是其雙親節點的左子樹,雙親節點為紅,叔叔節點為黑色,那麼我們把雙親節點右旋,再調整顏色,即可得到一顆平衡的紅黑樹。
- 如果插入的節點是其雙親節點的右子樹,雙親節點為紅,叔叔節點為黑色,我們先把雙親節點左旋,再把新的“雙親節點”右旋,調整顏色,即可得到平衡的紅黑樹。
- 若如4和5中,把雙親節點和叔叔節點紅黑調換,類似操作也可達到目的。
部分示意圖:
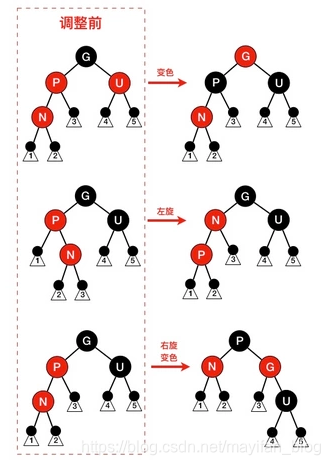
配圖展示了變色,左旋,右旋變色操作,大家可以在大腦裡模擬一下旋轉變色的動態過程,也建議動手畫畫,以促進理解。
紅黑樹的刪除我們這裡不細說,原理和插入類似,最重要的是我們要靈活運用旋轉和變色的方法,時刻保證紅黑樹滿足上述五條性質。
紅黑樹的定義(java實現)
這段程式碼展現了紅黑樹節點,顏色,指標等引數的定義。其中值得一提的是T引數的運用。我們知道,紅黑樹實現的是基本的二叉查詢樹,不論插入還是刪除,我們都需要尋找到相應位置,在這過程中我們需要不斷和節點值比較,確定索引的方向。程式中我用引數T繼承Comparable介面,把T作為鍵值,我們便可以作比較了。其中<? super T>用什麼作用呢?T extends Comparable表示T型別繼承此介面(但此介面只能被繼承一次),可用來比較,也許我們在這個程式中把這部分換為T也沒關係,但如果需要比較的型別複雜起來,有了繼承關係,那麼可能會導致程式報錯,如果換為<? super T>便允許有繼承關係,比如Animal extends Comparable成立的情況下我們還可以讓Dog繼承Animal並實現Dog extends Comparable,具體實現大家可以動手敲一下,便能看出區別了。
public class RBTree<T extends Comparable<? super T>>{
private RBTree<T> mroot; //根節點
private static final boolean RED = false; //紅色
private static final boolean BLACK= true; //黑色
public class RBTNode<T extends Comparable<? super T>>{ //T型別實現比較介面
boolean color; //顏色屬性
T key; //鍵值,可比較
RBTNode<T> left; //左子節點
RBTNode<T> right; //右子節點
RBTNode<T> parent; //雙親節點
public RBTNode(boolean color, T key, RBTNode<T> left, RBTNode<T> right,RBTNode<T> parent) {
this.color = color;
this.key = key;
this.left = left;
this.right = right;
this.parent = parent;
}
}
}
紅黑樹的操作(java實現)
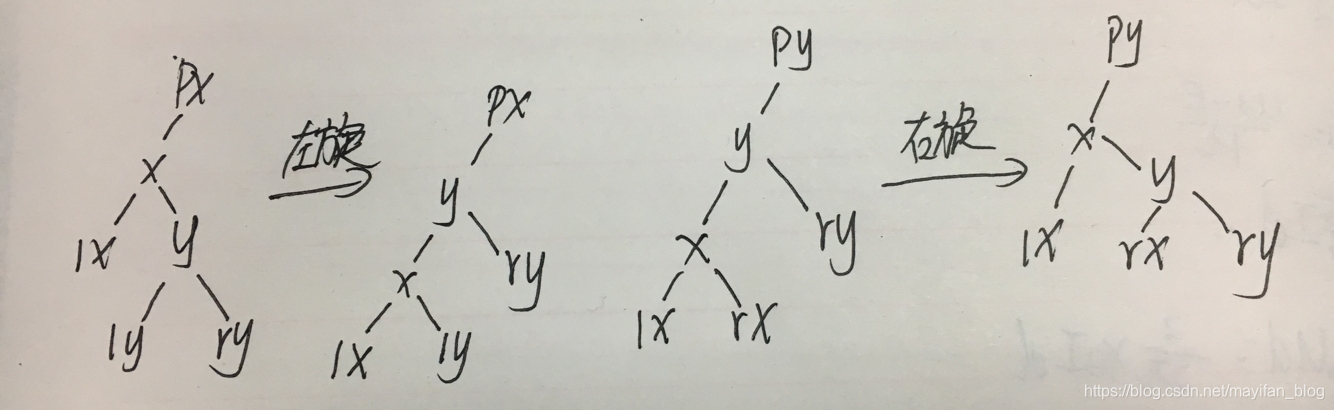
1、左旋:
private void leftRotate(RBTNode<T> x){ //左旋的方法
RBTNode<T> y = x.right; //把x的右子節點設為y節點
x.right=y.left; //x指向ly
if(y.left!=null)
y.left.parent=x; //ly指向lx節點
y.parent=x.parent; //y指向px
if(x.parent==null){
this.mRoot = y; //把y設為根節點
}else{
x.parent.left=y; //px指向y
}
x.parent=y;
y.left=x;
}
2、右旋:
private void rightRotate(RBTNode<T> y){ //右旋的方法
RBTNode<T> x= y.left;
x.parent=y.parent;
if(y.parent==null){
this.mRoot=x;
}else{
y.parent.left=x;
}
y.left=x.right;
if(x.right!=null)
x.right.parent=y;
x.right = y;
y.parent= x;
}
關於旋轉操作的程式碼實現,我們簡單介紹一下思路和寫程式碼的過程中可能需要注意的問題:我們首先需要畫出旋轉前後的示意圖,這有助於我們觀察判斷指標的變化。連線兩個節點一般需要兩步,既要把前一節點指向後一節點,也要把後一節點的雙親節點指標指向前一節點,主要有兩種操作:1、類似這種指標的賦值:y.left=x.right;2、指標指向節點:y.parent.left=x;我們只要在需要連線的節點之間重新建立連線即可完成節點的調整,這便是旋轉。我們需要注意到,如果涉及到類似這種操作:if(x.right!=null) x.right.parent=y;我們不要忘記加上非空判斷,防止出現物件空指標異常。
3、查詢:
通過結點的key值比較來判斷是接下來查詢左子樹還是右子樹。直到找到null位置,才停止,等待插入:
while (x != null) {
y=x;
cmp = node.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else
x = x.right;
}
4、插入:
獲取之前查詢的null位置的父節點的位置,和其鍵值比較,判斷插入左側還是右側,如果y為null,則插入為根節點。
node.parent = y;
if (y!=null) {
cmp = node.key.compareTo(y.key);
if (cmp < 0)
y.left = node;
else
y.right = node;
} else {
this.mRoot = node;
}
5、設定顏色,樹平衡修正(平衡修正的方法即根據上方介紹的幾種插入情況做分類討論):
// 設定節點的顏色為紅色
node.color = RED;
// 將它重新修正為一顆二叉查詢樹
insertFixUp(node);
6、輸入需要插入的鍵值,建立節點:
public void insert(T key) {
RBTNode<T> node=new RBTNode<T>(key,BLACK,null,null,null);
// 如果新建結點失敗,則返回。
if (node != null)
insert(node); //呼叫方法,找到位置,插入節點
}
我們在實現紅黑樹的旋轉,插入,刪除等方法後,便可以通過呼叫這些方法,來實現綜合性的操作。所有紅黑樹的操作,都要圍繞紅黑樹的五條基本性質來實現。
