推薦系統中的矩陣分解總結
最近學習矩陣分解,但是學了好多種類,都亂了,看了這篇文章,系統性的總結了矩陣分解,感覺很棒,故分享如下:
前言
推薦系統中最為主流與經典的技術之一是協同過濾技術(Collaborative Filtering),它是基於這樣的假設:使用者如果在過去對某些專案產生過興趣,那麼將來他很可能依然對其保持熱忱。其中協同過濾技術又可根據是否採用了機器學習思想建模的不同劃分為基於記憶體的協同過濾(Memory-based CF)與基於模型的協同過濾技術(Model-based CF)。其中基於模型的協同過濾技術中尤為矩陣分解(Matrix Factorization)技術最為普遍和流行,因為它的可擴充套件性極好並且易於實現
矩陣分解
對於推薦系統來說存在兩大場景即評分預測(rating prediction)與Top-N推薦(item recommendation,item ranking)。評分預測場景主要用於評價網站,比如使用者給自己看過的電影評多少分(MovieLens),或者使用者給自己看過的書籍評價多少分(Douban)。其中矩陣分解技術主要應用於該場景。Top-N推薦場景主要用於購物網站或者一般拿不到顯式評分資訊的網站,即通過使用者的隱式反饋資訊來給使用者推薦一個可能感興趣的列表以供其參考。其中該場景為排序任務,因此需要排序模型來對其建模。因此,我們接下來更關心評分預測任務。
對於評分預測任務來說,我們通常將使用者和專案(以電影為例)表示為二維矩陣的形式,其中矩陣中的某個元素表示對應使用者對於相應專案的評分,1-5分表示喜歡的程度逐漸增加,?表示沒有過評分記錄。推薦系統評分預測任務可看做是一個矩陣補全(Matrix Completion)的任務,即基於矩陣中已有的資料(observed data)來填補矩陣中沒有產生過記錄的元素(unobserved data)。值得注意的是,這個矩陣是非常稀疏的(Sparse),稀疏度一般能達到90%以上,因此如何根據極少的觀測資料來較準確的預測未觀測資料一直以來都是推薦系統領域的關鍵問題。
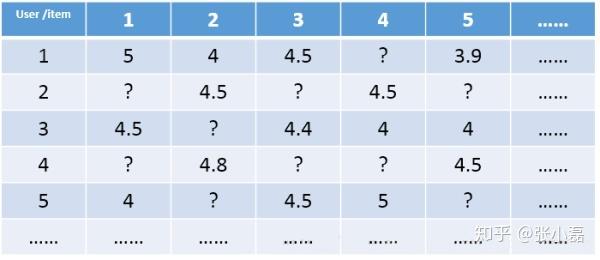
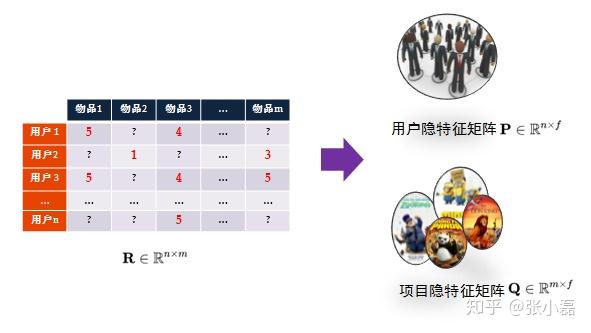
重點:推薦系統的評分預測場景可看做是一個矩陣補全的遊戲,矩陣補全是推薦系統的任務,矩陣分解是其達到目的的手段。因此,矩陣分解是為了更好的完成矩陣補全任務(欲其補全,先其分解之)。之所以可以利用矩陣分解來完成矩陣補全的操作,那是因為基於這樣的假設:假設UI矩陣是低秩的,即在大千世界中,總會存在相似的人或物,即物以類聚,人以群分,然後我們可以利用兩個小矩陣相乘來還原它。
1、PureSVD
當然提到矩陣分解,人們首先想到的是數學中經典的SVD(奇異值)分解,在這我命名為PureSVD(傳統並經典著),直接上公式:
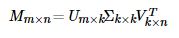
當然SVD分解的形式為3個矩陣相乘,左右兩個矩陣分別表示使用者/專案隱含因子矩陣,中間矩陣為奇異值矩陣並且是對角矩陣,每個元素滿足非負性,並且逐漸減小。因此我們可以只需要前 個因子來表示它。
如果想運用SVD分解的話,有一個前提是要求矩陣是稠密的,即矩陣裡的元素要非空,否則就不能運用SVD分解。很顯然我們的任務還不能用SVD,所以一般的做法是先用均值或者其他統計學方法來填充矩陣,然後再運用SVD分解降維。
2、FunkSVD
剛才提到的PureSVD首先需要填充矩陣,然後再進行分解降維,同時由於需要求逆操作(複雜度O(n^3)),存在計算複雜度高的問題,所以後來Simon Funk提出了FunkSVD的方法,它不在將矩陣分解為3個矩陣,而是分解為2個低秩的使用者專案矩陣,同時降低了計算複雜度:
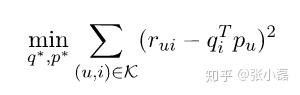
它借鑑線性迴歸的思想,通過最小化觀察資料的平方來尋求最優的使用者和專案的隱含向量表示。同時為了避免過度擬合(Overfitting)觀測資料,又提出了帶有L2正則項的FunkSVD:
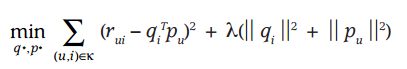
以上兩種最優化函式都可以通過梯度下降或者隨機梯度下降法來尋求最優解。
3、PMF
Salakhutdinov et al. Probabilistic matrix factorization. NIPS(2008): 1257-1264.
PMF是對於FunkSVD的概率解釋版本,它假設評分矩陣中的元素 是由使用者潛在偏好向量
和物品潛在屬性向量
的內積決定的,並且服從均值為
,方差為
的正態分佈:
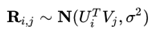
則觀測到的評分矩陣條件概率為:
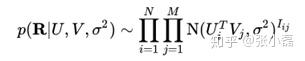
同時,假設使用者偏好向量與物品偏好向量服從於均值都為0,方差分別為 ,
的正態分佈:
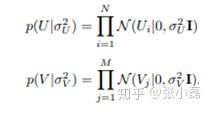
根據貝葉斯公式,可以得出潛變數U,V的後驗概率為:
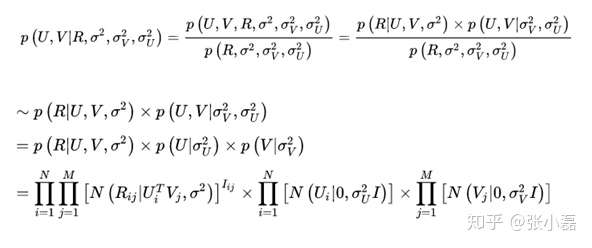
接著,等式兩邊取對數 後得到:
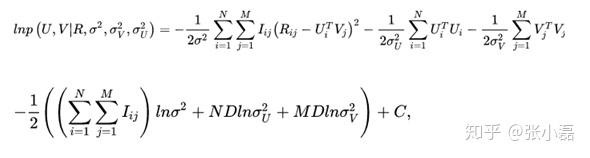
最後,經過推導,我們可以發現PMF確實是FunkSVD的概率解釋版本,它兩個的形式一樣一樣的。
注:為了方便讀者理解,在此舉例推導中間項 ,將此項展開,帶入多維正態分佈即可得到
。推導如下:

4、BiasSVD
Koren et al. Matrix factorization techniques for recommender systems.Computer 42.8 (2009).
在FunkSVD提出來之後,陸續又提出了許多變形版本,其中相對流行的方法是BiasSVD,它是基於這樣的假設:某些使用者會自帶一些特質,比如天生願意給別人好評,心慈手軟,比較好說話,有的人就比較苛刻,總是評分不超過3分(5分滿分);同時也有一些這樣的專案,一被生產便決定了它的地位,有的比較受人們歡迎,有的則被人嫌棄,這也正是提出使用者和專案偏置項的原因;項亮給出的解釋是:對於一個評分系統有些固有屬性和使用者物品無關,而使用者也有些屬性和物品無關,物品也有些屬性與使用者無關,具體的預測公式如下:
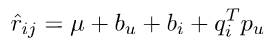
其中, 為整個網站的平均評分,是真個網站的基調;
為使用者的評分偏置,代表某個使用者的評分基調,
為專案的被評分偏置,代表某個專案的屬性基調。
5、SVD++
Koren Y. Factor in the neighbors: Scalable and accurate collaborative filtering[J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2010, 4(1): 1.
在使用者除了顯式評分外,隱式反饋資訊同樣有助於使用者的偏好建模,因此隨後提出了SVD++。它是基於這樣的假設:使用者除了對於專案的顯式歷史評分記錄外,瀏覽記錄或者收藏列表等隱反饋資訊同樣可以從側面一定程度上反映使用者的偏好,比如使用者對某個專案進行了收藏,可以從側面反映他對於這個專案感興趣,具體反映到預測公式為:
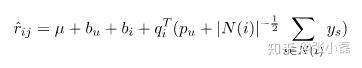
其中 為使用者
所產生隱反饋行為的物品集合;
為隱藏的對於專案
的個人喜好偏置,是一個我們所要學習的引數;至於
是一個經驗公式。
6、timeSVD
Koren et al. Collaborative filtering with temporal dynamics. Communications of the ACM 53.4 (2010): 89-97.
它是基於這樣的假設:使用者的興趣或者偏好不是一成不變的,而是隨著時間而動態演化。於是提出了timeSVD,其中使用者的和物品的偏置隨著時間而變化,同時使用者的隱含因子也隨著時間而動態改變,在此物品的隱含表示並未隨時間而變化(假設物品的屬性不會隨著時間而改變)。
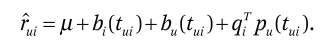
其中, 為時間因子,表示不同的時間狀態。
7、NMF
Lee et al. Learning the parts of objects by non-negative matrix factorization. Nature 401.6755 (1999): 788.
這是一篇發表在Nature上的經典論文,谷歌學術顯示引用將近9k,它提出了一個假設:分解出來的小矩陣應該滿足非負約束。
因為在大部分方法中,原始矩陣 被近似分解為兩個低秩矩陣
相乘的形式,這些方法的共同之處是,即使原始矩陣的元素都是非負的,也不能保證分解出的小矩陣都為非負,這就導致了推薦系統中經典的矩陣分解方法可以達到很好的預測效能,但不能做出像User-based CF那樣符合人們習慣的推薦解釋(即跟你品味相似的人也購買了此商品)。在數學意義上,分解出的結果是正是負都沒關係,只要保證還原後的矩陣元素非負並且誤差儘可能小即可,但負值元素往往在現實世界中是沒有任何意義的。比如影象資料中不可能存在是負數的畫素值,因為取值在0~255之間;在統計文件的詞頻時,負值也是無法進行解釋的。因此提出帶有非負約束的矩陣分解是對於傳統的矩陣分解無法進行科學解釋做出的一個嘗試。它的公式如下:
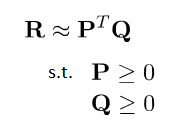
其中, ,
兩個矩陣中的元素滿足非負約束。
8、WMF
Pan et al. One-class collaborative filtering. ICDM, 2008.
Hu et al. Collaborative filtering for implicit feedback datasets. ICDM, 2008.
對於矩陣分解來說,我們一般是處理的推薦系統中的評分預測任務,但同樣矩陣分解也可以用來進行Top-N的推薦,即根據隱式資訊來預測使用者是否點選某專案。你可以把他看做是二分類問題,即點或者不點。但這不是普通的二分類問題,因為在模型訓練的過程中負樣本並非都為真正的負樣本,可能是使用者根本沒見過該專案,何來喜不喜歡,沒準他看到後喜歡呢,即正樣本告訴我們作者喜歡的資訊,但負樣本並不能告訴我們該使用者不喜歡。由於只存在正樣本,所以我們把只有正反饋的問題定義為one-class問題,即單類問題。對於單類問題,該作者提出了兩種解決策略,一種是加權的矩陣分解,另一種是負取樣技術。雖然只是加了一下權重,看起來比較naive,但在於當時的研究背景下,這一小步其實是推薦系統中的一大步。
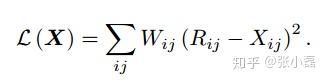
對於單類問題的研究一直沒有停止過,雖然負取樣技術是啟發式的,即不用通過資料建模的方式來進行預測,但效果還是很好用的。最近幾年人們提出了基於模型的方法來處理這種單類問題,即從缺失資料中來進行建模,具體可參見這兩篇論文【Hernández-Lobato et al 2014,Liang et al 2016】。
10、LLORMA
Lee et al. Local low-rank matrix approximation.ICML. 2013.
經典的矩陣分解模型是假設整個使用者-專案矩陣(即UI矩陣)滿足低秩假設(即全域性低秩假設),即在整個系統當中,使用者和專案總是滿足存在相似的某種模式,即物以類聚,人以群分。
這種假設固然有道理,但在當今大資料時代下,全域性意義上的低秩假設似乎太強了,尤其是在資料量巨大的情況下(即使用者數與專案數都很多的系統當中),因此該論文推翻了全域性意義上經典的全域性低秩假設,它認為大千世界,林林總總,我們應該去尋找區域性的低秩假設(即區域性低秩假設)。首先根據某種相似測度來將整個大矩陣分為若干個小矩陣,每個小矩陣當中滿足某種相似度閾值,然後再在區域性的小矩陣當中做低秩假設。這樣,全域性的大矩陣可以由多個區域性的小矩陣來加權組合構成,具體可參見該論文。
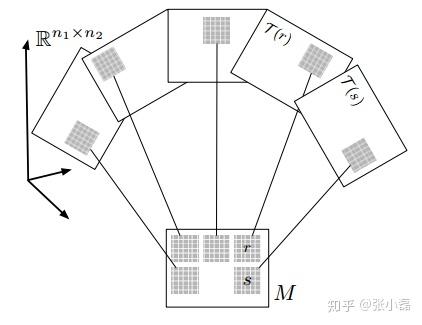
11、SRui
Ma Hao. An experimental study on implicit social recommendation. SIGIR, 2013.
雖然經典的矩陣分解方法已經可以到達比較好的預測效能了,但它固有的弊病仍然是躲不開的,即資料稀疏與冷啟動問題。為了緩解資料稀疏我們可以引入豐富的社交資訊。即如果兩個使用者是朋友關係,那麼我們假設他們有相同的偏好,同時他們學得的使用者隱表示在向量空間應該有相近的距離。使用者維度如此,同理,專案維度亦可以利用此思路來約束專案隱表示。即如果兩個專案之間的關係較近,那麼在低維向量空間中的距離同樣也應該較小。這裡的專案關係是從UI矩陣中抽取出來的,論文中成為專案隱社交關係(其實專案維度跟社交沒啥關係)。具體公式如下:
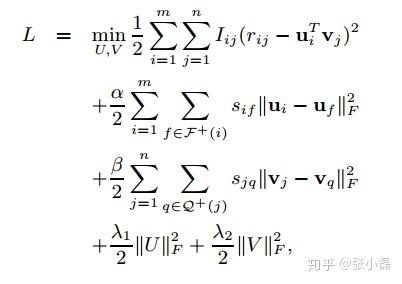
其中, 表示使用者
和使用者
的社交相似度,
表示專案
與專案
的隱社交相似度,在使用者維度和專案維度分別增加了平滑項約束,使得學得的隱特徵表示更加符合現實意義。
12、ConvMF
Kim et al. Convolutional matrix factorization for document context-aware recommendation. RecSys 2016.
當然矩陣分解的優點之一是可擴充套件性好,這當然不是吹的,比如16年的這篇文章就是將矩陣分解(MF)與影象處理領域很火的卷積神經網路(CNN)做了完美結合。
矩陣分解作為協同過濾模型中經典的方法,效能當然沒的說。但它存在的資料稀疏與冷啟動問題一直以來都是它的痛點,因此結合外部豐富的資訊成為了緩解上述問題的有效途徑。其中文字資料作為web中主流的資料形式成為了首選,並且對於文字的處理,大部分還是基於one-hot的表示,因此無法捕捉文件中上下文的關鍵資訊,於是作者將兩者做了結合,具體細節請參見論文,該公式如下:
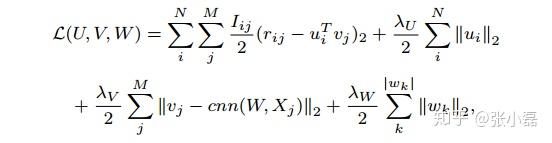
其中,在使得使用者隱向量與專案隱向量做內積儘可能逼近真實評分的同時,對專案隱向量做了額外約束,即讓專案隱向量跟CNN學得的文件特性儘可能的接近。
13、NCRPD-MF
Hu et al. Your neighbors affect your ratings: on geographical neighborhood influence to rating prediction. SIGIR 2014.
剛才說到,MF的可擴充套件性好,一方面是可以和主流模型做無縫整合,另一方面是可以和多種資訊源做特徵融合,比如14年的這篇文章,它是融合了文字評論資訊,地理鄰居資訊,專案類別資訊以及流行度等資訊,具體預測公式如下:
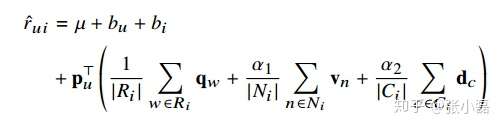
其中, 為文字特徵的低維向量表示,
為地理鄰居的低維向量表示,
為專案類別的低維特徵表示。
總結
首先因為低秩假設,一個使用者可能有另外一個使用者與他線性相關(物品也一樣),所以使用者矩陣完全可以用一個比起原始UI矩陣更低維的矩陣表示,pureSVD就可降維得到兩個低維矩陣,但是此方法要求原始矩陣稠密,因此要填充矩陣(只能假設值),因此有了funkSVD直接分解得到兩個低維矩陣。因為使用者,物品的偏置愛好問題所以提出了biasSVD。因為使用者行為不僅有評分,且有些隱反饋(點選等),所以提出了SVD++。因為假設使用者愛好隨時間變化,所以提出了timeSVD。因為funkSVD分解的兩個矩陣有負數,現實世界中不好解釋,所以提出了NMF。為了符合TopN推薦,所以提出了WMF。推翻低秩假設,提出了LLORMA(區域性低秩)。因為以上問題都未解決資料稀疏和冷啟動問題,所以需要用上除了評分矩陣之外的資料來使推薦更加豐滿,即加邊資訊。
