在推薦場景中, 我們可以把user對item的行為, 用評分矩陣R∈R|U|×|P|$R\in {\mathbb{R}}^{|U|\times |P|}$表示.
U={user}$U=\{user\}$,為使用者集合, P={item}$P=\{item\}$, 為item集合.
以商品為例,比如說使用者u1對商品p1加購物車, 那就令 Ru1,p1=3$R_{u1,p1}=3$, 使用者u1對商品p2做出購買行為, 那就令 Ru1,p2=5$R_{u1,p2}=5$.

問題描述

在真實場景中, 使用者只會對部分item做出反饋, 所以矩陣是非常稀疏的.
推薦的task就是預測出使用者可能感興趣的未見商品.
我們假設使用者喜歡某個商品是因為使用者的特徵偏好與該商品的特徵能夠吻合起來.
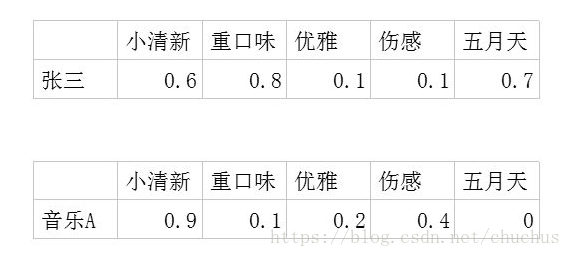
那這些特徵是什麼呢? 以音樂推薦為例, 見圖1

這些特徵我們不必人為定義, 可以引入latent space的假定, 有k$k$個潛在的特徵.
使用者對每個特徵都有一個偏好程度, 用矩陣Q$Q$表示, 每個物品都有一個特徵的吻合程度, 用P$P$表示,所以我們的任務就是求出這兩個矩陣, 然後對R$R$進行補全, 找出得分高的未見商品推薦給使用者.

問題定義

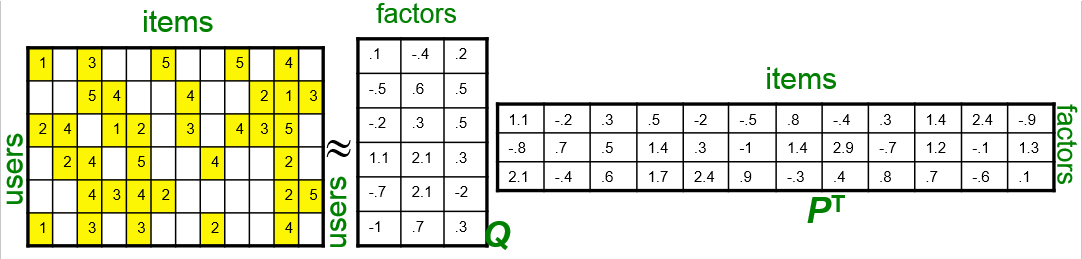
figure 矩陣分解示意, 網路盜圖,符號跟上面公式不一樣

求解方法

參考