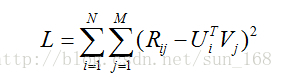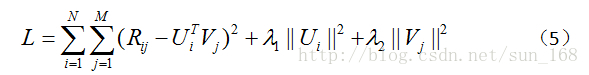推薦系統是當下越來越熱的一個研究問題，無論在學術界還是在工業界都有很多優秀的人才參與其中。近幾年舉辦的推薦系統比賽更是一次又一次地把推薦系統的研究推向了高潮，比如幾年前的Neflix百萬大獎賽，KDD CUP 2011的音樂推薦比賽，去年的百度電影推薦競賽，還有最近的阿里巴巴大資料競賽。這些比賽對推薦系統的發展都起到了很大的推動作用，使我們有機會接觸到真實的工業界資料。我們利用這些資料可以更好地學習掌握推薦系統，這些資料網上很多，大家可以到網上下載。

        推薦系統在工業領域中取得了巨大的成功，尤其是在電子商務中。很多電子商務網站利用推薦系統來提高銷售收入，推薦系統為Amazon網站每年帶來30%的銷售收入。推薦系統在不同網站上應用的方式不同，這個不是本文的重點，如果感興趣可以閱讀《推薦系統實踐》（人民郵電出版社，項亮）第一章內容。下面進入主題。

       為了方便介紹，假設推薦系統中有使用者集合有6個使用者，即U={u1,u2,u3,u4,u5,u6}，專案（物品）集合有7個專案，即V={v1,v2,v3,v4,v5,v6,v7}，使用者對專案的評分結合為R，使用者對專案的評分範圍是[0, 5]。R具體表示如下：

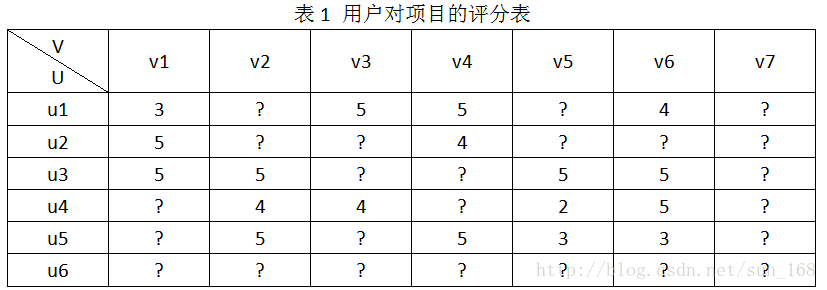
       推薦系統的目標就是預測出符號“？”對應位置的分值。推薦系統基於這樣一個假設：使用者對專案的打分越高，表明使用者越喜歡。因此，預測出使用者對未評分專案的評分後，根據分值大小排序，把分值高的專案推薦給使用者。怎麼預測這些評分呢，方法大體上可以分為基於內容的推薦、協同過濾推薦和混合推薦三類，協同過濾演算法進一步劃分又可分為基於基於記憶體的推薦（memory-based）和基於模型的推薦（model-based），本文介紹的矩陣分解演算法屬於基於模型的推薦。

        矩陣分解演算法的數學理論基礎是矩陣的行列變換。在《線性代數》中，我們知道矩陣A進行行變換相當於A左乘一個矩陣，矩陣A進行列變換等價於矩陣A右乘一個矩陣，因此矩陣A可以表示為A=PEQ=PQ（E是標準陣）。

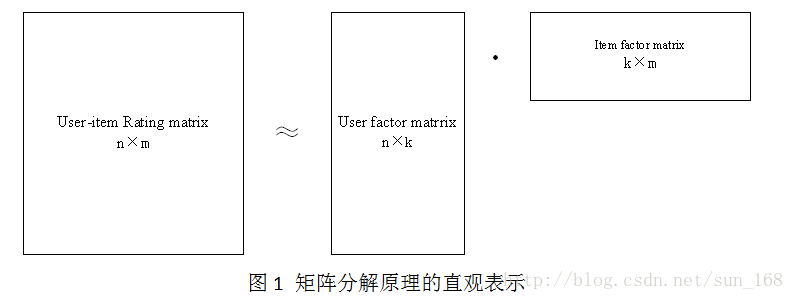
       矩陣分解目標就是把使用者-專案評分矩陣R分解成使用者因子矩陣和專案因子矩陣乘的形式，即R=UV，這裡R是n×m， n =6， m =7，U是n×k，V是k×m。直觀地表示如下：

       高維的使用者-專案評分矩陣分解成為兩個低維的使用者因子矩陣和專案因子矩陣，因此矩陣分解和PCA不同，不是為了降維。使用者i對專案j的評分r_ij =innerproduct(u_i, v_j)，更一般的情況是r_ij =f

(U_i, V_j)，這裡為了介紹方便就是用u_i和v_j內積的形式。下面介紹評估低維矩陣乘積擬合評分矩陣的方法。

      首先假設，使用者對專案的真實評分和預測評分之間的差服從高斯分佈，基於這一假設，可推匯出目標函式如下：

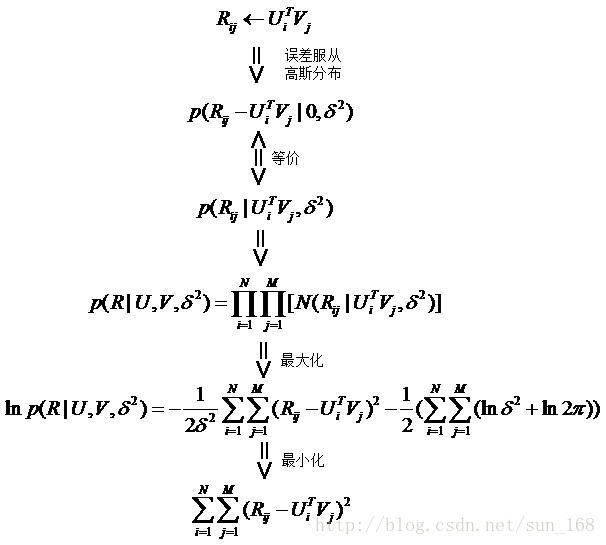
最後得到矩陣分解的目標函式如下：

       從最終得到得目標函式可以直觀地理解，預測的分值就是儘量逼近真實的已知評分值。有了目標函式之後，下面就開始談優化方法了，通常的優化方法分為兩種：交叉最小二乘法（alternative least squares）和隨機梯度下降法（stochastic gradient descent）。

      首先介紹交叉最小二乘法，之所以交叉最小二乘法能夠應用到這個目標函式主要是因為L對U和V都是凸函式。首先分別對使用者因子向量和專案因子向量求偏導，令偏導等於0求駐點，具體解法如下：

       上面就是使用者因子向量和專案因子向量的更新公式，迭代更新公式即可找到可接受的區域性最優解。迭代終止的條件下面會講到。

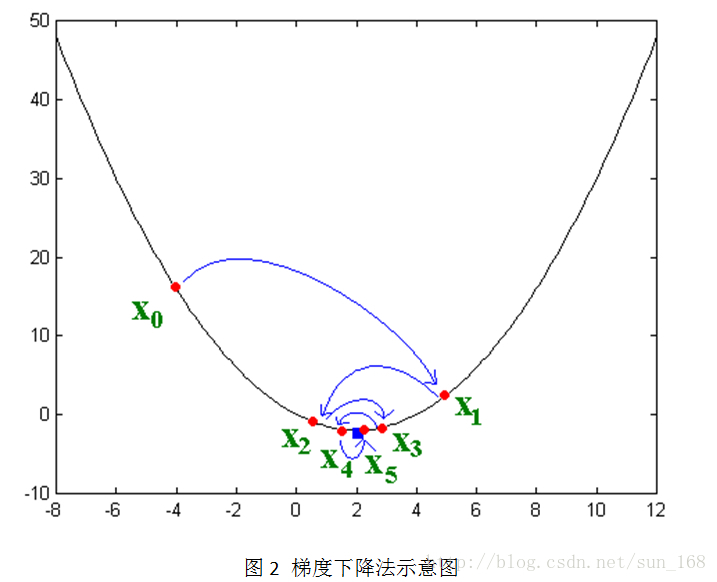
       接下來講解隨機梯度下降法，這個方法應用的最多。大致思想是讓變數沿著目標函式負梯度的方向移動，直到移動到極小值點。直觀的表示如下：

     其實負梯度的負方向，當函式是凸函式時是函式值減小的方向走；當函式是凹函式時是往函式值增大的方向移動。而矩陣分解的目標函式L是凸函式，因此，通過梯度下降法我們能夠得到目標函式L的極小值（理想情況是最小值）。

     言歸正傳，通過上面的講解，我們可以獲取梯度下降演算法的因子矩陣更新公式，具體如下：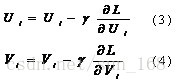

（3）和（4）中的γ指的是步長，也即是學習速率，它是一個超引數，需要調參確定。對於梯度見（1）和（2）。

下面說下迭代終止的條件。迭代終止的條件有很多種，就目前我瞭解的主要有

1）    設定一個閾值，當L函式值小於閾值時就停止迭代，不常用

2）    設定一個閾值，當前後兩次函式值變化絕對值小於閾值時，停止迭代

3）    設定固定迭代次數

       另外還有一個問題，當用戶-專案評分矩陣R非常稀疏時，就會出現過擬合（overfitting）的問題，過擬合問題的解決方法就是正則化（regularization）。正則化其實就是在目標函式中加上使用者因子向量和專案因子向量的二範數，當然也可以加上一範數。至於加上一範數還是二範數要看具體情況，一範數會使很多因子為0，從而減小模型大小，而二範數則不會它只能使因子接近於0，而不能使其為0，關於這個的介紹可參考論文Regression Shrinkage and Selection via the Lasso。引入正則化項後目標函式變為：

    

（5）中λ_1和λ_2是指正則項的權重，這兩個值可以取一樣，具體取值也需要根據資料集調參得到。優化方法和前面一樣，只是梯度公式需要更新一下。

矩陣分解演算法目前在推薦系統中應用非常廣泛，對於使用RMSE作為評價指標的系統尤為明顯，因為矩陣分解的目標就是使RMSE取值最小。但矩陣分解有其弱點，就是解釋性差，不能很好為推薦結果做出解釋。

      後面會繼續介紹矩陣分解演算法的擴充套件性問題，就是如何加入隱反饋資訊，加入時間資訊等。

引用：

說明上圖 圖2摘自李金屏課件