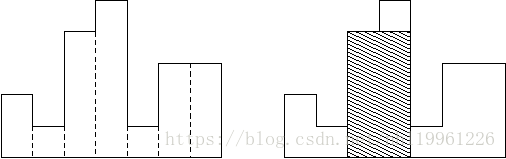
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, …, hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

思路：單調棧，寫的時候還不太會，想著想著就弄懂了。
首先是，我想到了單調遞增子序列，才想到了這種思路（單調棧），因為遇到遞減的時候就可以更新最大的矩陣了，並且更新剛放進去的點的長度，因為你放進去的數是小於棧頭的元素的。

程式碼：

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include<string.h>
#include <map>
#include<stack>
#include <vector>
#include <set>
#include <math.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+9;
struct node
{
    ll id;
    ll h;
}a[maxn];
stack<node>s;

int main()
{
    ll n;
    while(~scanf("%lld",&n),n)
    {
        while(!s.empty())s.pop();
        node p;
        ll ans=-1;//最終答案
        for(ll i=1; i<=n; i++)
        {
            scanf("%lld",&a[i].h);//高度
            a[i].id=i;//原始的位置
        }
        a[n+1].h=0,a[n+1].id=(ll)n+1;//加一個最小的，以便在最後將棧清空
        for(ll i=1; i<=n+1; i++)
        {
            ll x=a[i].h;
            if(s.size()==0||s.top().h<x)//嚴格的單調遞增
                s.push(a[i]);
            else
            {
                while(!s.empty()&&s.top().h>=x)//小於等於它的，全去掉
                {
                    node p1=s.top();
                    s.pop();
                    a[i].id=p1.id;//更新a[i]的位置，因為他們都比a[i]高
                    ll len=(ll)i-p1.id;
                    if(len*p1.h>ans)//更新最大值
                        ans=len*p1.h;
                }
                s.push(a[i]);
            }
        }
        printf("%lld\n",ans);
    }
    return 0;
}