1、大數定律的理解

簡而言之，大數定律告訴我們在隨機事件的大量重複出現中，往往呈現幾乎必然的規律，在試驗不變的條件下，重複試驗多次，隨機事件的概率近似於它出現的頻率。

大數定律以嚴格的數學形式表現了隨機現象最根本的性質之一：平均結果的穩定性。

       我們用卡方分佈來驗證這種穩定性如下圖，開始在小樣本情況下，樣本均值非常的不穩定，但是當樣本量繼續增大後，樣本均值的收斂性已經非常的明顯，基本收斂到均值3附近。

        在我們的生活中處處可以看到有趣的大數定律

一位人口統計學家調查發現，歐洲各地的男嬰與女嬰的出生比例是22:21，但是發現法國巴黎的比例是25:24，這非常小的差別促使他決心去搞個明白。最後驚人的發現，當時巴黎重女輕男，一些人會丟棄男嬰，經過一些修正後，巴黎的這個比例依然是22:21。而中國的歷次人口普查的結果也是22:21。

        既然我們在強調大數定律的嚴格數學形式，下面我們會給出大數定律數學定義：

        首先我們要知道大數定律依照收斂的形式分為強大數定律和弱大數定律

弱大數定律

我們依然畫圖來描述弱大數定律

        上圖虛線部分表示一個任意小的實數，每條實線表示一個數列，可以看到當樣本不斷增加後，數列會逐漸收斂到虛線部分裡面，偶然會有幾條跑出來。這個就叫做弱大數定律的依概率收斂。

強大數定律

我們依然畫圖來描述強大數定律

相比較弱大數定律，強大數定律表徵著當數列樣本量增大後，它再也不會超出虛線所表示的邊界，也就是超出這個邊界的概率就是0了。這個就叫做強大數定律的處處收斂。

蒙特卡洛方法

轉自：https://blog.csdn.net/saltriver/article/details/52194918

       蒙特卡洛方法（Monte Carlo method，也有翻譯成“蒙特卡羅方法”）是以概率和統計的理論、方法為基礎的一種數值計算方法，將所求解的問題同一定的概率模型相聯絡，用計算機實現統計模擬或抽樣，以獲得問題的近似解，故又稱隨機抽樣法或統計試驗法。上述就是蒙特卡洛方法的基本概念，比較抽象，下面結合實際工作中的理解，談一談對蒙特卡洛方法的一些認識。

（1）首先，蒙特卡洛不是個人名，而是個地名，說明該方法與概率有著密切的關聯。

       蒙特卡洛方法的提出者是大名鼎鼎的數學家馮·諾伊曼，搞計算機的不可能不知道他（計算機之父），馮·諾伊曼在20世紀40年代中期用馳名世界的賭城—摩納哥的蒙特卡洛來命名這種方法。（大家也別把蒙特卡洛當一個城市，估計和北京的一條街差不了多少，因為摩納哥（不是非洲的摩洛哥）本身就是個袖珍國家，比我國澳門都小的多）。說明該方法與賭博中的隨機性、概率性有著天然而密切的聯絡。幾乎涉及到複雜的、與概率相關的數值計算的領域都有可能會用到。比如計算物理、經濟金融、統計學、機器學習等。

（2）蒙特卡洛沒有什麼高深的理論，它只是一種方法或者說策略。

       蒙特卡洛方法並沒有什麼高深的理論支撐，如果一定要說有理論也就只有概率論或統計學中的大數定律了。蒙特卡洛的基本原理簡單描述是先大量模擬，然後計算一個事件發生的次數，再通過這個發生次數除以總模擬次數，得到想要的結果。比如投3個骰子，計算3個骰子同時是6的概率，可以模擬投N次（隨機樣本數），統計同時是6出現的次數C，然後C除以N即是計算結果。

（3）蒙特卡洛方法可以應用在很多場合，但求的是近似解，在模擬樣本數越大的情況下，越接近與真實值，但樣本數增加會帶來計算量的大幅上升。    

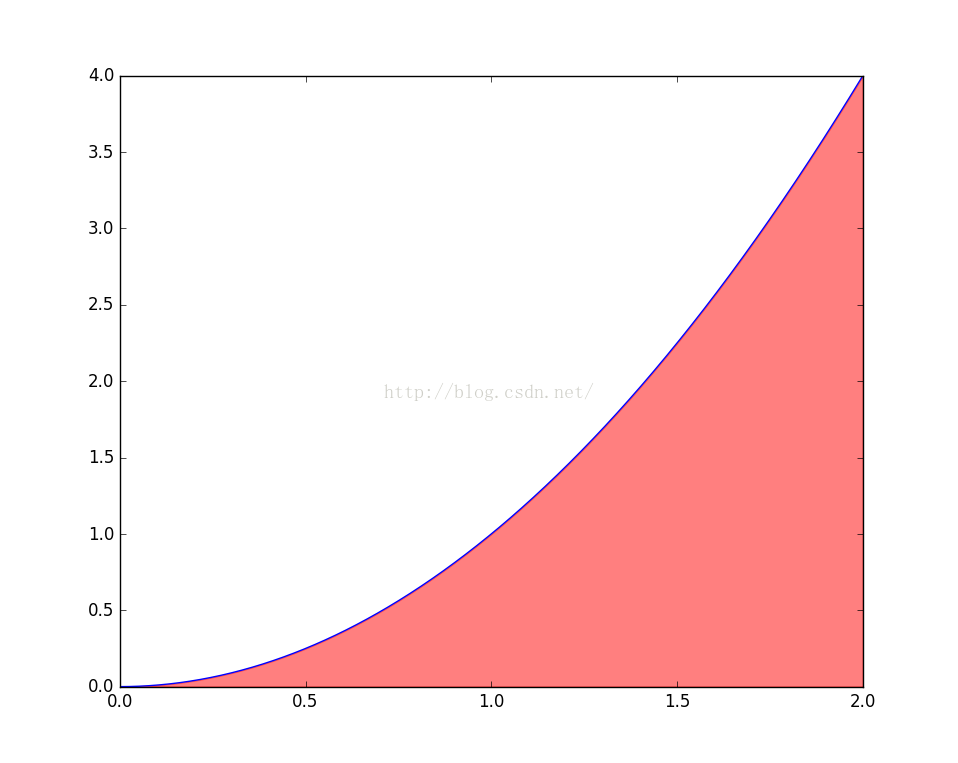
       蒙特卡洛方法不僅僅是算概率哦，再看一個稍複雜點的例項：求函式y=x2在[0,2]區間的積分，即求如下圖所示的紅色區域的面積。當然直接用數學中的定積分公式算更簡單精確，這裡主要是舉例說明下蒙特卡洛方法的使用過程。

繪圖程式碼如下：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2, 1000)
y = x ** 2
plt.plot(x, y)
plt.fill_between(x, y, where=(y > 0), color='red', alpha=0.5)
plt.show()

    該紅色區域在一個2×4的正方形裡面。使用蒙特卡洛方法，隨機在這個正方形裡面產生大量隨機點（數量為N），計算有多少點（數量為count）落在紅色區域內（判斷條件為y<x2），count/N就是所要求的積分值，也即紅色區域的面積。

    1.模擬1000個隨機點：

NN = 1000
points = [[xy[0] * 2, xy[1] * 4] for xy in np.random.rand(N, 2)]
plt.scatter([x[0] for x in points], [x[1] for x in points], s=5, c=np.random.rand(N), alpha=0.5)

plt.show()

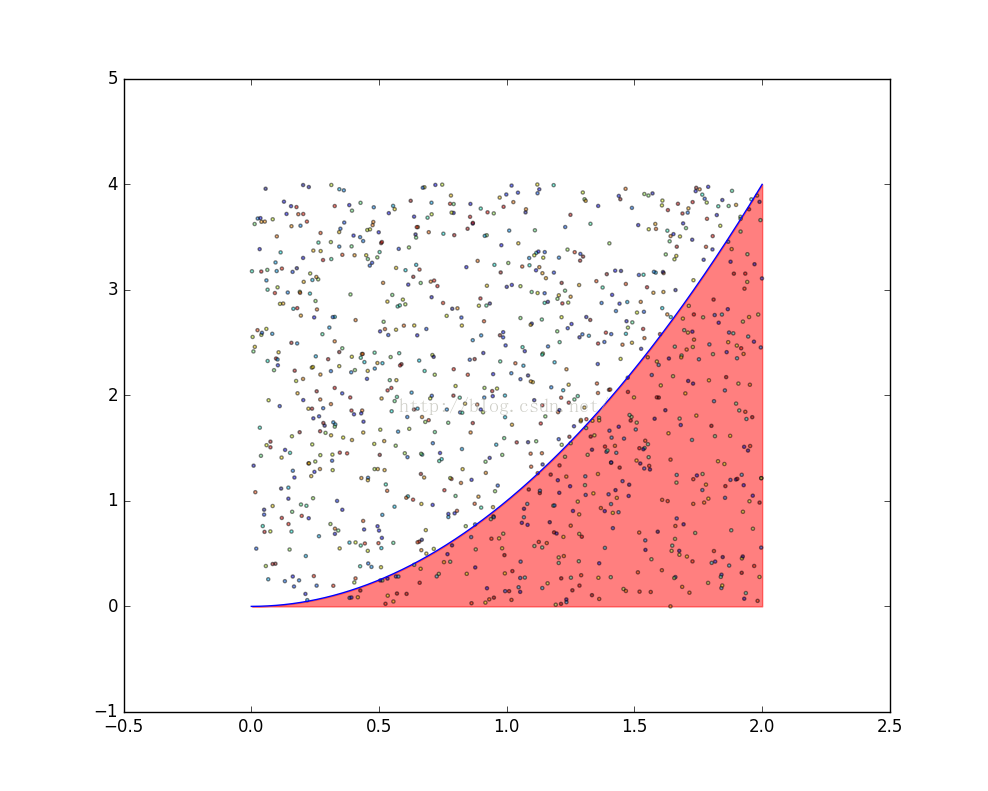
    2.計算落在紅色區域的比重：

count = 0
for xy in points:
    if xy[1] < xy[0] ** 2:
        count += 1
print((count / N) * (2 * 4))

輸出結果：

2.832

    這與精確值（2.666666）的差距只有6.2%，而對於更大規模的模擬，N=100萬，輸出結果為：2.66528，這與精確值的差距只有0.051975%（萬分之五）。可以看出，蒙特卡洛方法有一定的誤差，誤差的大小與模擬的樣本大小直接相關，模擬樣本越大，誤差越小，但計算量也會大幅上升。

（4）對於簡單問題來說，蒙特卡洛是個“笨”辦法。但對許多問題來說，它往往是個有效，有時甚至是唯一可行的方法。

       對於上面的簡單問題，蒙特卡洛方法就顯得有點“笨”了。直接用數值積分運算更簡單，更精確。

       print(scipy.integrate.quad(lambda x: x ** 2, 0, 2)[0])

       輸出結果：

       2.666666666666667

       但對於涉及不可解析函式或概率分佈的模擬及計算，蒙特卡洛方法是個有效的方法。

        我們都玩過套圈圈的遊戲，想過為什麼你總是套不上嗎？用蒙特卡洛方法來算一算。

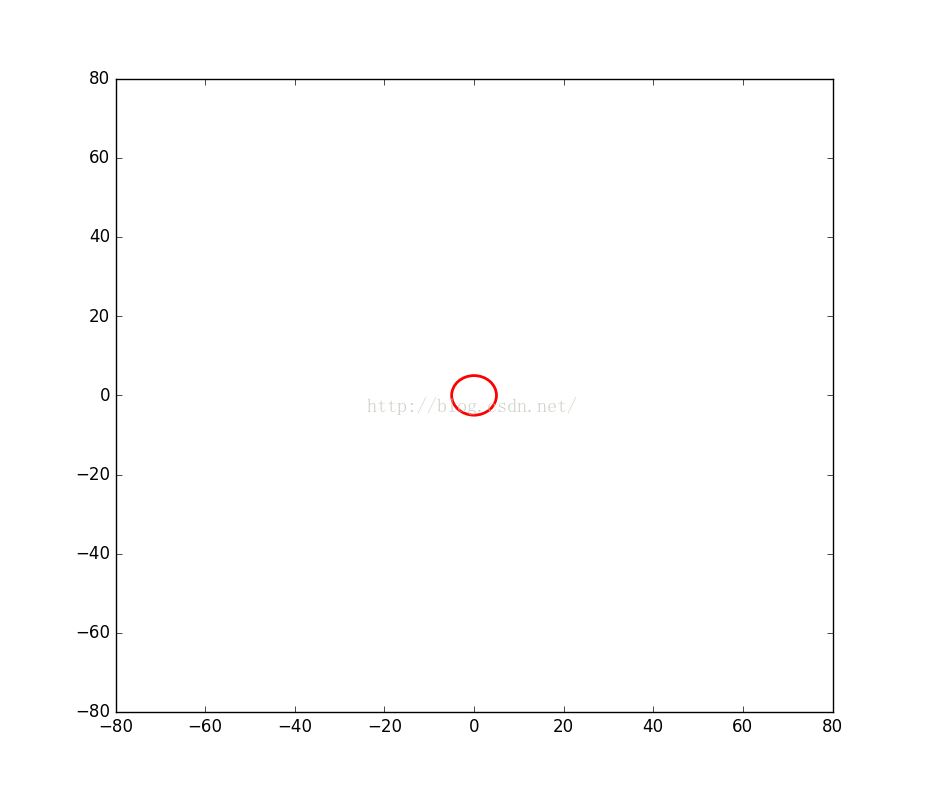
        1.設物品中心點座標為（0,0），物品半徑為5cm。

         import matplotlib.pyplot as plt
         import matplotlib.patches as mpatches
         import numpy as np
         circle_target = mpatches.Circle([0, 0], radius=5, edgecolor='r', fill=False)
         plt.xlim(-80, 80)
         plt.ylim(-80, 80)
         plt.axes().add_patch(circle_target)

         plt.show()

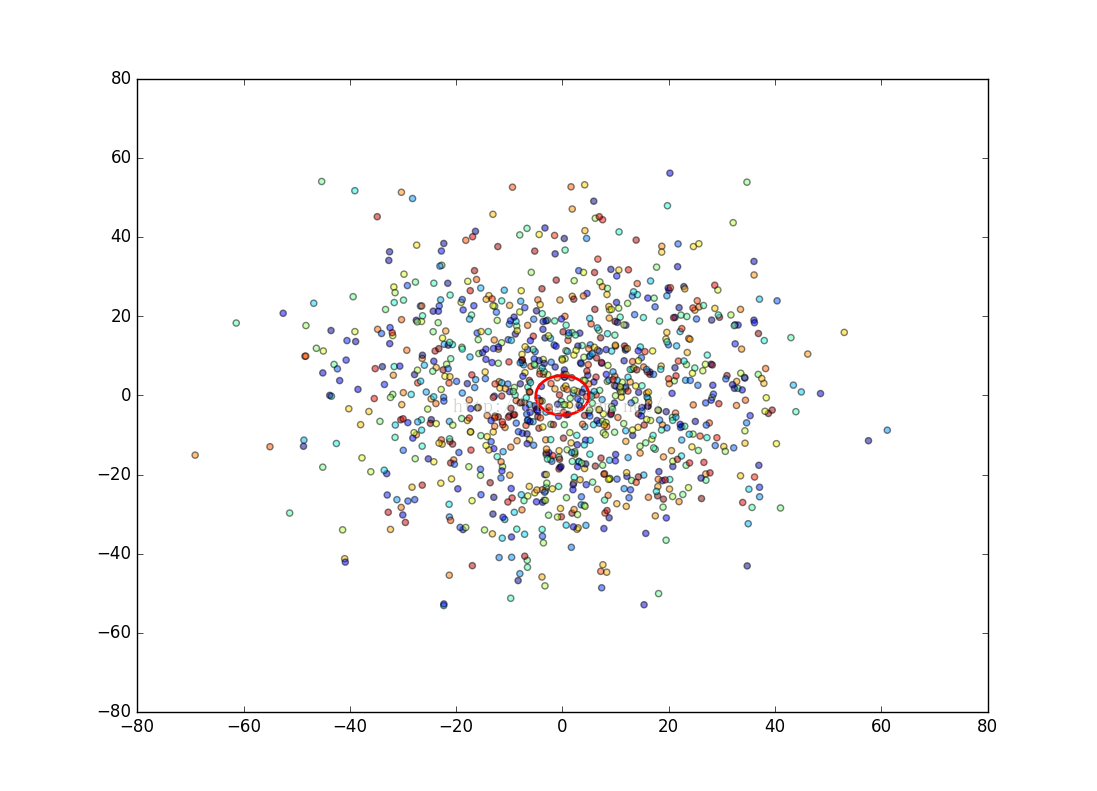
    2.設投圈半徑8cm，投圈中心點圍繞物品中心點呈二維正態分佈，均值μ=0cm，標準差σ=20cm，模擬1000次投圈過程。

       N = 1000
       u, sigma = 0, 20
       points = sigma * np.random.randn(N, 2) + u

       plt.scatter([x[0] for x in points], [x[1] for x in points], c=np.random.rand(N), alpha=0.5)

    上圖中紅圈為物品，散點圖為模擬1000次投圈過程中，投圈中心點的位置散佈。

    3.計算1000次投圈過程中，投圈套住物品的佔比情況。

    print(len([xy for xy in points if xy[0] ** 2 + xy[1] ** 2 < (8-5) ** 2]) / N)

    輸出結果：0.014，即投1000次，有14次能夠套住物品，就是個小概率事件，知道你為什麼套不住了吧。

（5）蒙特卡洛方法本身不是優化方法，與遺傳演算法、粒子群等優化演算法有著本質的區別。

       蒙特卡洛方法與遺傳演算法、粒子群演算法等智慧優化演算法有相似之處，比如都屬於隨機近似方法，都不能保證得到最優解等，但它們也有著本質的差別。一是層次不一樣，蒙特卡洛只能稱之為方法，遺傳演算法等則屬於仿生智慧演算法，比蒙特卡洛方法要複雜。二是應用領域不同，蒙特卡洛是一種模擬統計方法，如果問題可以描述成某種統計量的形式，那麼就可以用蒙特卡洛方法來解決；遺傳演算法等則適用於大規模的組合優化問題（選址問題、排班問題、管理排程、路線優化）等，以及複雜函式求最值、引數優化等。