比賽連結
本題解同步於洛谷部落格

獲獎名單

前三：
rank1:@GZY_GZY
rank2:@ljc1301
rank3:@加藤惠
orz三位dalao！tql！

一血榜：
A: @ThinkofBlank（09:05:39）
B: @muller（09:08:57）
C: @GZY_GZY（11:34:05）
D: @東師附中大頭（10:57:32）
E: @GZY_GZY（18:29:35獲得最高分58pts）

吐槽

誰知道我元旦想放水題放出鍋了啊……T2據說是和別人差不多的題……對此我深表歉意。（既然這是基本全場AC的簽到題大家就放我一馬吧，感激不盡2333）
其它題應該沒啥問題。

還有某人特別喜歡抄別人程式碼，不是我針對你，抄一題就算了，你T3T4T5都是抄的，在這裡做個警告，你拿了高分又如何，別以為改了變數名函式名我就看不出來，別以為開了完全隱私保護就NB了。

總體評估

T1,T2簡單題，T3,T4稍有難度，T5較難（可能不太準？）部分分放的真的好多好多啊……
好了廢話不多說，放題解。

T1 WD與矩陣

subtask1:

暴力即可。複雜度 $O(T$

subtask2:

這個部分分是腦子一抽給的，肯定沒人寫。直接列舉列，把行的狀態狀壓起來就行。複雜度 $O$

subtask3:

打表應該都能發現，答案就是 $2^{(n-1)(m-1)}$，因為我們可以最後一行和最後一列完全可以根據前面填的值直接算出來，因此任意排列前面的東西即可。複雜度 $O(Tlogn)$。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int mod = 998244353;
ll modpow(ll a, ll b) {
    ll res = 1;
    for (; b; b >>= 1) {
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
    }
    return res;
}
int main(){
    int n, m, T;
    scanf("%d", &T);
    while (T--) {
        scanf("%d%d", &n, &m);
        printf("%lld\n", modpow(2, (ll)(n - 1) * (m - 1)));
    }
    return 0;
}

T2 WD與迴圈

subtask1:

我們會顯然的發現問題轉化為求有多少種不同的值使 $\sum_{i=1}^na_i\le m$。因此這個直接dp即可。
$f[i][j]$表示當前到第 $i$個迴圈，前面值的和為 $j$的方案數，最後就是 $\sum_{i=0}^mf[n][i]$，複雜度 $O(nm+T)$.

subtask2:

發現有不等號不太方便，考慮如果是等號怎麼做。這是顯然的插板法（如果不知道可以度娘……），也就是說 $\sum_{i=1}^na_i=m$的非負解共有 $\binom{n+m-1}{m-1}$組，因為我們可以視為在 $n$個數中加上 $m-1$個可相鄰的隔板，相鄰兩個隔板之間的長度就代表了對應的數字。
因此我們預處理階乘，直接列舉 $m$計算對應的組合數，然後求和即可。複雜度 $O(Tm+mod)$。

subtask3:

有個結論，就是：
$\sum_{i=q}^n \binom{i}{q}=\binom{n+1}{q+1}$
簡略證明如下：
$\sum_{i=q}^n\binom{i}{q}=\binom{n}{q}+\binom{n}{q+1}即\sum_{i=q}^{n-1}\binom{i}{q}=\binom{n}{q+1}$
歸納即可。
因此原題的答案直接就是 $\binom{n+m}{m}$，直接上盧卡斯定理即可。複雜度 $O(T+mod)$。（假定盧卡斯求組合數為 $O(1)$）。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int mod = 19491001;
ll fac[mod], rev[mod], n, m;
ll modpow(ll a, int b) {
    ll res = 1;
    for (; b; b >>= 1) {
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
    }
    return res;
}
ll lucas(ll a, ll b) {
    if (a < b) return 0;
    if (a < mod) return fac[a] * rev[b] % mod * rev[a - b] % mod;
    return lucas(a / mod, b / mod) * lucas(a % mod, b % mod) % mod;
}
int main() {
    for (int i = fac[0] = 1; i < mod; i++) fac[i] = fac[i - 1] * i % mod;
    rev[mod - 1] = modpow(fac[mod - 1], mod - 2);
    for (int i = mod - 1; i > 0; i--) rev[i - 1] = rev[i] * i % mod;
    int T; scanf("%d", &T);
    while (T--) {
        scanf("%lld%lld", &n, &m);
        printf("%lld\n", lucas(n + m, m));
    }
    return 0;
}

T3 WD與數列

subtask1:

似乎 $O(n^3)$暴力直接可以把subtask2艹過去？luogu還是太快了啊！這個應該不用多說吧，直接暴力列舉一對開頭，然後暴力向後擴充套件直到相減的值改變了。

subtask2:

本來這個點是給hash的……又怕hash常數大被卡，於是就只有1000的資料量……不管不管送分大甩賣！
（我看你是送分大甩鍋吧2333）
首先可以想到差分整個序列，然後問題轉化為求不相交不相鄰的相等子串對數。
就是列舉答案的長度，然後從左往右跑，對於某個串，把他左邊和他不相交或相鄰的串的hash加到hash_map裡，直接看有多少串的hash和它相同即可。複雜度 $O(n^2)$。

subtask3:

嘿嘿嘿這個點沒法水過去了吧……
做法1： 肯定還是差分整個數列，接下來考慮怎麼做。如果去掉不相交不相鄰的這個限制直接SA+單調棧即可（或者SAM，但是慢啊）。接下來考慮如何把多算的減掉。
我們會發現多算的一定靠的很近（廢話），可以考慮使用NOI2016優秀的拆分那題的方法，也就是使用調和級數。

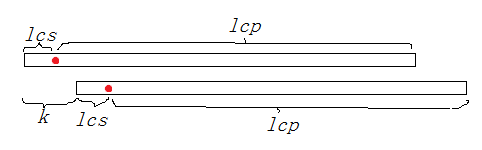
我們考慮列舉兩個串的偏移位置（即圖中的 $k$），然後每 $k$位打一個點，可以發現我們只需要讓這兩個串在它們第一次出現紅點的位置被計算一次即可。
考慮計算兩個紅點為結尾的LCS和為開頭的LCP，由於我們要讓每對串只能在第一個紅點處被計算，因此LCS要和 $k$取個min。然後就是細節功底了……考慮暴力怎麼做，我們可以列舉兩個串的開頭位置 $a,a+k$，並且由於兩個串要相鄰或相交，則第一個串的結尾 $ 相關推薦 洛谷比賽 waaadreamer的聖誕虐題賽題解 比賽連結 本題解同步於洛谷部落格 獲獎名單 前三： rank1:@GZY_GZY rank2:@ljc1301 rank3:@加藤惠 orz三位dalao！tql！ 一血榜： A: @ThinkofBlank（09:05:39） B: @muller（09:08:57） C: @ 洛谷比賽-P5011 水の造題-題解 題目地址與題意見連結 暴力就是 O ( k 洛谷—— P1926 小書童——刷題大軍 基礎 描述 amp class for ons 輸入輸出 dash print https://www.luogu.org/problem/show?pid=1926#sub 題目背景 數學是火，點亮物理的燈；物理是燈，照亮化學的路；化學是路，通向生物的坑；生物是坑，埋 洛谷 P1926 小書童——刷題大軍 i++ show 哲學 輸出格式 時間 for mes 數學 blank 題目背景 數學是火，點亮物理的燈；物理是燈，照亮化學的路；化學是路，通向生物的坑；生物是坑，埋葬學理的人。 文言是火，點亮歷史宮燈；歷史是燈，照亮社會之路；社會是路，通向哲學大坑；哲學是坑，埋葬文科 洛谷 P1311 選擇客棧 —— 水題 ret += return https pac col 位置 show names 題目：https://www.luogu.org/problemnew/show/P1311 看每個位置能否成為咖啡店，然後作為客棧和前面配對即可。 代碼如下： #include<i 洛谷P1072 Hankson 的趣味題(數學) etc tps oid long long esp amp har con http 題意 題目鏈接 Sol 充滿套路的數學題。。 如果你學過莫比烏斯反演的話不難得到兩個等式 \[gcd(\frac{x}{a_1}, \frac{a_0}{a_1}) = 1\] \[gcd 洛谷-機器翻譯-NOIP2010提高組復賽 原理 中文 turn 英文單詞 。。 printf 100% P20 otto 題目背景 小晨的電腦上安裝了一個機器翻譯軟件，他經常用這個軟件來翻譯英語文章。 題目描述 這個翻譯軟件的原理很簡單，它只是從頭到尾，依次將每個英文單詞用對應的中文含義來替換。對於每個英文單 洛谷1072 Hankson 的趣味題（素數） 題意 求gcd(a0,x)=a1且lcm(b0,x)=b1中x的解的方案數。 題解 這種gcd的問題一般都要拆成質因數來分析。 線篩出1~sqrt(2e9)中的素數，那麼所有數的質因數一定在其中出現，不然它本身就是一個素數（這個要特判）。 對於質數p，他們的次數分別為ca0,ca1, 洛谷 P3709 大爺的字串題 解題報告 題目描述 給你一個字串a，每次詢問一段區間的貢獻 貢獻定義： 每次從這個區間中隨機拿出一個字元x，然後把x從這個區間中刪除，你要維護一個集合S 如果S為空，你rp減1 如果S中有一個元素不小於x，則你rp減1，清空S 之後將x插入S 由於你是大爺，平時做過的題考試都會考到，所以每次詢問你搞完這段 【題解】洛谷P4902[CYJian的水題大賽[第三彈]]C.乘積 線性篩 題目連結 賽後題解 講道理，中間那些公式變形看明白了，線性篩那段給我搞蒙了……h是算啥的，為啥要%(mod-1) QAQ #include<cstdio> const int mod=19260817,N=1e6+10; int t,a,b,p 洛谷比賽數學題*1 zlh秒的題，我根本不會，出題人欽點此題提高-，想來我要爆零了。。。 這題n，a都巨大無比，所以演算法要儘量往k身上靠，先推一波式子： 把這裡sigma內的東西拆開得到： 第k此項係數C(k,k)肯定是1，消去，再換一下i，j列舉順序： 這裡就 洛谷比賽【泯滅：整除】 題目連結 官方的題解看不懂，問了Shone{\rm Shone}Shone終於聽懂了，感覺是一個很神奇的方法，所以就記一下了。 首先題目要求求出xm≡x(modn)x^m\equiv x({\rm mod\ }n)xm≡x(modn)的方程的解的個數，其中x∈[ 洛谷 P4343 [SHOI2015]自動刷題機 ## 思路 > 二分答案 顯然的二分答案，但是因為二分判定條件 $\text{wa}$ 了好幾遍…… 可以發現，$n$ 越大，$k$ 就越小，所以答案是有單調性的，因此可以用兩個二分，一次求最大值，一次求最小值，這裡以求最大為例。 判定一個答案是否可行可以線性掃一遍直接求，在判定中記錄過的題數 $cnt 洛谷 P1596 [USACO10OCT]湖計數Lake Counting 題解 for stream lin ger recent lines 輸入輸出格式 lac figure 此文為博主原創題解，轉載時請通知博主，並把原文鏈接放在正文醒目位置。 題目鏈接：https://www.luogu.org/problem/show?pid=1596 洛谷 P1226 取余運算||快速冪 題解 代碼 amp base iostream div 其中 tro std strong 此文為博主原創題解，轉載時請通知博主，並把原文鏈接放在正文醒目位置。 題目鏈接：https://www.luogu.org/problem/show?pid=1226 題目描述 洛谷 P2397 yyy loves Maths VI (mode) 題解 clas 由於 http 讀下 dba lov 格式 輸出格式 否則 此文為博主原創題解，轉載時請通知博主，並把原文鏈接放在正文醒目位置。 題目鏈接：https://www.luogu.org/problem/show?pid=2397 題目背景 自動上次redb 洛谷 P1828 香甜的黃油 Sweet Butter 題解 分析 org har 16px emp oid head 最優 ems 此文為博主原創題解，轉載時請通知博主，並把原文鏈接放在正文醒目位置。 題目鏈接：https://www.luogu.org/problem/show?pid=1828 題目描述 農夫John發 洛谷P1854 花店櫥窗布置 分析+題解代碼 一道 文件的 using 設置 固定 algo 一個數 stream 不同的 洛谷P1854 花店櫥窗布置 分析+題解代碼 蒟蒻的第一道提高+/省選-，紀念一下。 題目描述： 某花店現有F束花，每一束花的品種都不一樣，同時至少有同樣數量的花瓶，被按順序擺成一行，花瓶的位置 洛谷3919：可持久化數組——題解 isdigit getchar() targe namespace 就會 sdi pro ont pan https://www.luogu.org/problemnew/show/P3919 如題，你需要維護這樣的一個長度為 N 的數組，支持如下幾種操作 BZOJ1229 & 洛谷2917：[USACO2008 NOV]toy 玩具 & 洛谷4480：[BJWC2018]餐巾計劃問題——題解 n) trie clas try new 假設 \n 最優 一個 標題很長emmm…… [USACO2008 NOV]toy 玩具 https://www.luogu.org/problemnew/show/P2917 https://ww $