因為是傻瓜式教程，所以一定會非常詳細！一些概念link到了Wiki的相應解釋上。 
歡迎捉蟲~！

二分類和迴歸的關係

考慮x⇒y 表示的二分類或迴歸問題，其中x 是輸入，y 是輸出。 
1. 在二分類中，y 的值取0或1，代表被分為正類或負類。在迴歸中，y 的取值為連續值。 
2. 線上性迴歸模型中，y=wTx=w⋅x，此處w 為引數向量，x 為輸入樣本向量。 
3. 進一步，廣義線性迴歸模型可以寫為g(y)=w⋅x 或者 y=g−1(w⋅x)的形式，其中g 為單調可微函式。所以在對數迴歸中，模型是ln(y)=w⋅x。

sigmoid函式與LR的關係

sigmoid函式

：在數學上是擁有性感的s形曲線樣子的函式: 

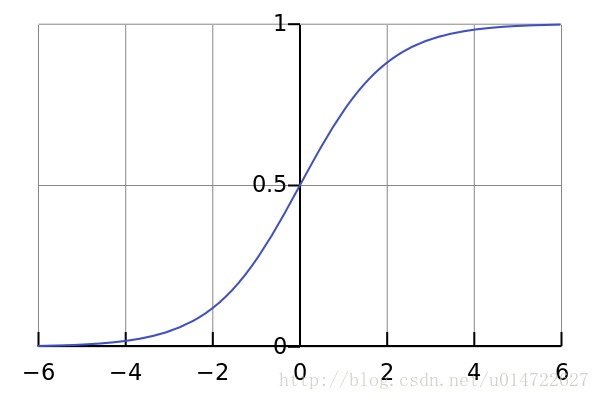
通常說的sigmoid函式指的是這個logistic函式：δ(z)=11+e−z=ez1+ez 。本文所指的sigmoid函式就是該logistic函式： 

sigmoid函式具有以下特點： 
- 值域在(0,1) 
- 求導非常容易δ′(z)=δ(1−δ(z)) (求導過程見附錄，或Wiki)

我們希望在做二分類時，輸出y 不再是非0即1的取值，而是希望輸出一個有概率意義的(0,1) 之間的值，表示的是分為正類的概率（所以1−y是分為負類的概率），然後再做二分類，所以我們挑選sigmoid函式作為廣義線性迴歸的g−1，即

y

=δ(w⋅x)=11+e−w⋅x(1) 接下來將符合 y=g−1(w⋅x) 形式的(1) 寫為

相關推薦

logistic regression（LR）對數機率迴歸 / 邏輯迴歸 公式推導

因為是傻瓜式教程，所以一定會非常詳細！一些概念link到了Wiki的相應解釋上。  歡迎捉蟲~！ 二分類和迴歸的關係 考慮x⇒y 表示的二分類或迴歸問題，其中x 是輸入，y 是輸出。  1. 在二分類中，y 的值取0或1，代表被分為正類或負類。在迴歸中，y 的取值為連續值。  2. 線上

【原創】Logistic regression （邏輯迴歸） 概述

 Logistic regression （邏輯迴歸）是當前業界比較常用的機器學習方法，用於估計某種事物的可能性。比如某使用者購買某商品的可能性，某病人患有某種疾病的可能性，以及某廣告被使用者點選的可能性等。（注意這裡是：“可能性”，而非數學上的“概率”，logis

機器學習作業-Logistic Regression（邏輯迴歸）

ML課堂的第二個作業，邏輯迴歸要求如下： 資料集連結如下： 邏輯迴歸的關鍵是運用了sigmod函式，sigmod函式有一個很好的性質是其導函式很好求 函式影象： sigmod會將函式值對映到（0，1）區間內，將其輸出值看作是概率則有邏輯迴歸的二分類模型

Logistic Regression（邏輯迴歸）

介紹 邏輯迴歸雖然稱為迴歸，但它卻是一個分類演算法，一個用來解決二分類問題的演算法，它通過將線性迴歸預測出的值對映到 {0,1} 上來實現分類的（0叫做負類，1叫做正類）。這是一個很簡單的二分類演算法，它的思想也很容易理解。 邏輯迴歸與線性迴歸的流程很相似：

最詳細的基於R語言的Logistic Regression（Logistic迴歸）原始碼，包括擬合優度，Recall，Precision的計算

這篇日誌也確實是有感而發，我對R不熟悉，但實驗需要，所以簡單學了一下。發現無論是網上無數的教程，還是書本上的示例，在講Logistic Regression的時候就是給一個簡單的函式及輸出結果說明。從來都沒有講清楚幾件事情： 1. 怎樣用訓練資料訓練模型，然後在測試資料

邏輯迴歸（LR）和支援向量機（SVM）的區別和聯絡

1. 前言 在機器學習的分類問題領域中，有兩個平分秋色的演算法，就是邏輯迴歸和支援向量機，這兩個演算法個有千秋，在不同的問題中有不同的表現效果，下面我們就對它們的區別和聯絡做一個簡單的總結。 2. LR和SVM的聯絡 都是監督的分類演算法。 都是線性分類方法 (不考慮核函式時）。 都是判別

邏輯迴歸（LR） 演算法模型簡介

邏輯迴歸（Logistic Regression）是機器學習中的一種分類模型，由於演算法的簡單和高效，在實際中應用非常廣泛。本文作為美團機器學習InAction系列中的一篇，主要關注邏輯迴歸演算法的數學模型和引數求解方法，最後也會簡單討論下邏輯迴歸和貝葉斯分類的關係，以及在多

logistic regression（二項 logistic 與 多項logistic ）

邏輯斯蒂迴歸 基本思想 數學推導 基於R的案例 結論 基本思想 這一講給大家介紹一下，廣義線性迴歸模型當中的一個最為典型的模型，邏輯斯底迴歸（logistic regression）。估計大家都見過。我們最長用到的是二值邏輯斯底迴歸，多項邏輯斯底書

長短期記憶（LSTM）系列_1.1、迴歸神經網路在時間序列預測中的介紹和應用

摘要，通過本文你可以學到： 傳統的時間序列預測方法側重於具有線性關係的單變數資料以及固定和手動診斷的時間依賴性。 神經網路增加了學習可能的噪聲和非線性關係的能力，其中任意定義但固定數量的輸入和輸出支援多變數和多步預測。 遞迴神經網路增加了有序觀察的顯式處理和從上下文學習時間依賴

ML：Scikit-Learn 學習筆記（3） --- Nearest Neighbors 最近鄰 迴歸及相關演算法

1 最近鄰迴歸 最近鄰迴歸是用在標籤值是連續取值的場景智商的，而不是離散取值，而是用最近鄰迴歸進行查詢的點，最後得到的結果是其所有最近鄰居的平均值。 scikit-learn 在迴歸部分，同樣實現了兩種迴歸演算法，和之前的一樣，和KNN思想近似的KNeigh

spark機器學習筆記：（六）用Spark Python構建迴歸模型

博主簡介：風雪夜歸子（英文名：Allen），機器學習演算法攻城獅，喜愛鑽研Meachine Learning的黑科技，對Deep Learning和Artificial Intelligence充滿興趣，經常關注Kaggle資料探勘競賽平臺，對資料、Machi

深度學習入門實戰（二）-用TensorFlow訓練線性迴歸

TensorFlow是谷歌爸爸出的一個開源機器學習框架，目前已被廣泛應用，谷歌爸爸出品即使效能不是最強的（其實效能也不錯），但絕對是用起來最方便的，畢竟谷歌有Jeff Dean坐鎮，這波穩。 0x01 TensorFlow安裝 官方有一個Mac上TensorFlow

我的spark學習之路（三）：利用spark做迴歸分析

spark的機器學習庫（MLlib）下有簡單的迴歸分析方法，今天只說最簡單的線性迴歸，spark提供有兩個迴歸分析庫（mllib和ml），我學習的時候在網上也查了不少資料，有一個奇怪的現象是網上關於spark迴歸分析的資料基本全是mllib，關於ml的基本沒見到

OpenCV學習筆記（一）對數變換

關於對數變換，目的就是將輸入影象中較窄的低灰度值對映到輸出影象較寬的灰度值。s=log(1+r); 在程式中使用add(InputArray src1, InputArray src2, OutputArray dst, InputArray mask=noArray()

Keras學習（六）——RNN迴圈神經網路迴歸

本文主要介紹使用RNN來實現迴歸，對曲線進行預測。 示例程式碼： import numpy as np from keras.datasets import mnist from keras.utils import np_utils from keras.models

跟著Andrew Ng挑戰Machine Learning（第三週）Part 1：邏輯迴歸簡介

注意： 　　我發現當我在閱讀其他大神&前輩們發表的文章時，往往只有前二十分鐘能夠集中注意力。之後就慢慢的會有些懈怠了，而往往他們付出的心血可能主要就集中在中後半部分⊙﹏⊙‖∣° 。 　　有鑑於此，我決定以後發的博文儘可能的短。呵呵呵呵呵呵……

【機器學習基本理論】詳解最大似然估計（MLE）、最大後驗概率估計（MAP），以及貝葉斯公式的理解

總結 ora 二次 判斷 天都 特性 以及 解釋 意思 【機器學習基本理論】詳解最大似然估計（MLE）、最大後驗概率估計（MAP），以及貝葉斯公式的理解 https://mp.csdn.net/postedit/81664644 最大似然估計（Maximum lik

ceph（3）--Ceph 物理和邏輯結構

gre network 鏡像 操作記錄 share 速度 深度優先 cache 訪問 本系列文章會深入研究 Ceph 以及 Ceph 和 OpenStack 的集成： （1）安裝和部署 （2）Ceph RBD 接口和工具 （3）Ceph 物理和邏輯結構 （4）Ceph 的

Logistic迴歸原理及公式推導

Logistic迴歸為概率型非線性迴歸模型，是研究二分類觀察結果與一些影響因素之間關係的一種多變量分析方法。通常的問題是，研究某些因素條件下某個結果是否發生，比如醫學中根據病人的一些症狀來判斷它是否患有某種病。   在講解Logistic迴歸理論之前，我們先從LR分類器說起。LR分類器

例項詳解js閉包（一）閉包基本概念及其作用推導

　　在學習前端的過程中，不可避免的要學習到js閉包這個知識點，很多朋友感到對閉包很難理解，也不清楚它有什麼用。本文就詳細介紹一下閉包，並通過幾個小例子來說明下閉包的用處。  一、閉包的概念       閉包的英文單詞是Closure，我先給閉包可