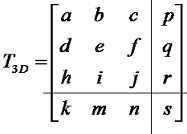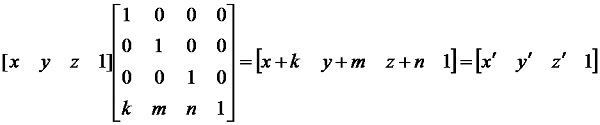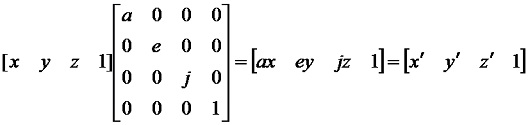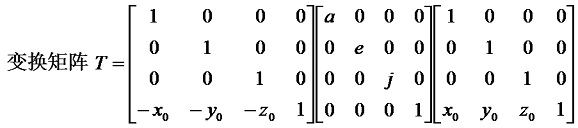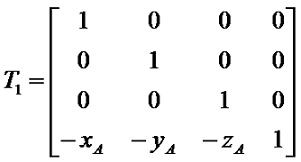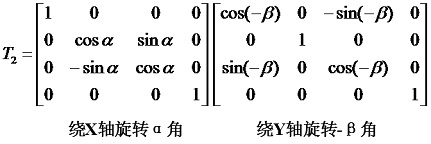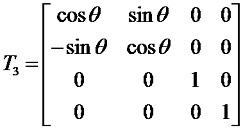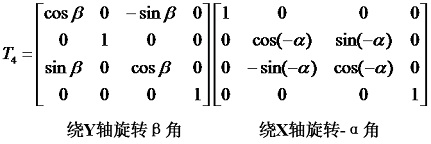(17)三維圖形幾何變換
三維圖形幾何變換是二維圖形幾何變換的擴充套件。在三維空間中,用規範化齊次座標[x y z 1]表示三維點,變換原理是把齊次座標點(x, y, z, 1)通過變換矩陣變換成新的齊次座標點(x’ y’, z’, 1),即:
[x y z 1] T3D = [x' y' z' 1]
因此,三維圖形的基本變換矩陣用4×4階矩陣表示,即:
1)左上角的3*3子塊實現比例、旋轉、對稱、錯切等基本變換;
2)左下角的1*3子塊實現平移變換;
3)右上角的3*1子塊實現透視變換;
4)右下角的1*1子塊實現全比例變換。
平移變換:
立體圖形上的任意一點(x, y, z)沿X軸、Y軸、Z軸方向分別平移k、m和n後,成為新圖形上的一點(x’, y’, z’),則有:x’=x+k y’=y+m z’=z+n
即:
比例變換:
1、相對於座標原點的比例變換,沿X、Y、Z軸方向的比例係數分別為a、e、j,則有:
當變換矩陣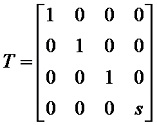
2、相對於任意點(x0, y0, z0)的比例變換,比例係數為a、e、j:
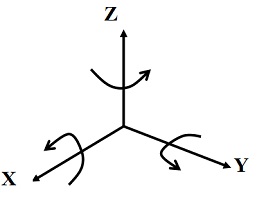
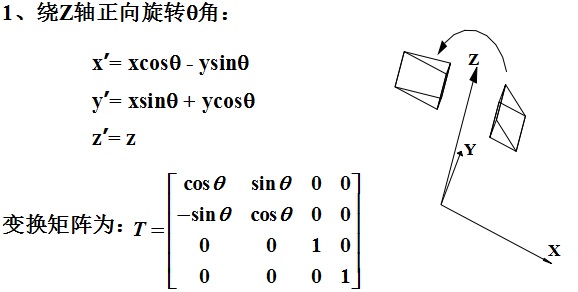
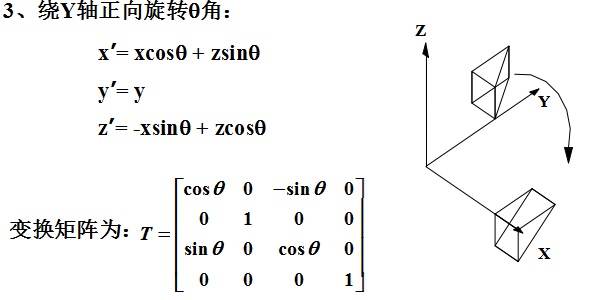
旋轉變換
旋轉的正方向:右手拇指指向轉軸正向,其餘四指纏繞方向便是θ角正向。
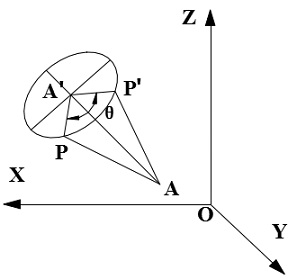
繞空間任意一條直線的旋轉:
設空間一條直線段AA'作為旋轉軸,A點座標是(xA, yA, zA),A'點座標是(x'A, y'A, z'A),空間一點P(x, y, z)繞AA'軸旋轉θ角到P'(x', y', z'),即:
[x' y' z' 1] = [x y z 1]*T
其中,T 為繞任意軸的旋轉變換矩陣,它由若干個基本變換矩陣組合而成。
第1步:將點P與旋轉軸AA'一起作平移變換,使旋轉軸AA'過原點,A與原點重合,變換矩陣為:
第2步:令AA'軸首先繞X軸逆時針旋轉α角,使其與XOZ平面共面,然後再繞Y軸順時針旋轉β角,使其與Z軸重合,變換矩陣為:
其中,α和β角可通過旋轉軸AA'的兩個端點座標計算得到。
第3步:將點P繞Z軸(即AA’軸)旋轉θ角,變換矩陣為:
第4步:作第2步的逆變換,即將AA'軸旋轉回到原來的位置,變換矩陣為:
第5步:作第1步的逆變換,即將旋轉軸AA'平移回到原來的位置,變換矩陣為:
因此,繞空間任意軸的旋轉變換矩陣為:
T = T1*T2*T3*T4*T5
對稱變換
1、關於X軸對稱:x不變,y、z相反2、關於Y軸對稱:y不變,x、z相反
3、關於Z軸對稱:z不變,x、y相反
4、關於座標原點對稱:x、y、z相反
5、關於XOY平面對稱:x、y不變,z相反
6、關於XOZ平面對稱:x、 z不變,y相反
7、關於YOZ平面對稱:y、 z不變,x相反
錯切變換

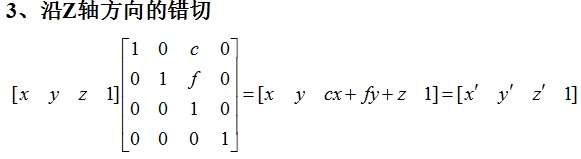
由錯切變換結果看出,一個座標的變化會受另外兩個座標的影響。