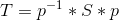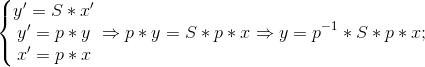參考資料：https://en.wikipedia.org/wiki/Matrix_similarity

這裡僅針對三維重建過程中的座標系變換進行個人理解。

在三維重建過程中，計算的位姿在不同座標系下的結果也是不同的（理所當然的吧），但是在工作中往往需要將它們變換成同一座標系下。座標點的變換很簡單，只需要乘以一個對應的變換矩陣即可。那麼如果以變換矩陣的形式來表示的話，在新的座標系下能否算出一個新的對應的變換矩陣呢？如何將他們進行有效的轉換是一個有效的trick。

假設在最初的座標系下，有

                                                                          y= T * x;

x是三維座標；T是一個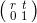的4*4矩陣;y是經過變換後的位置。

那麼對應的在另一個對應的座標系下，有

                                                                          y`= S * x`;

x`,y`是x,y在新的座標系下對應的座標；S是對應的變換矩陣（這裡我們要求的也是這個S和T之間的關係）。

在上面情況下，必然也有y`=p*y, x`=p*x;

所以  ;