最大子矩陣

Time Limit: 30000/10000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4459    Accepted Submission(s): 2306


Problem Description 給你一個m×n的整數矩陣，在上面找一個x×y的子矩陣，使子矩陣中所有元素的和最大。
Input 輸入資料的第一行為一個正整數T，表示有T組測試資料。每一組測試資料的第一行為四個正整數m,n,x,y（0<m,n<1000 AND 0<x<=m AND 0<y<=n），表示給定的矩形有m行n列。接下來這個矩陣，有m行，每行有n個不大於1000的正整數。
Output 對於每組資料，輸出一個整數，表示子矩陣的最大和。
Sample Input 1 4 5 2 2 3 361 649 676 588 992 762 156 993 169 662 34 638 89 543 525 165 254 809 280
Sample Output 2474

思路：動態規劃

狀態dp[i][j]代表長i寬j的矩陣的元素和。

（dp[i][j]+=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]）

假設要求找出x長y寬的最大子矩陣

在i>=x且j>=y的矩陣中找的話，

dp[i][j]就是包含a[i][j]元素的子矩陣的元素和，

則dp[i][j]-dp[i][j-y]-dp[i-x][j]+dp[i-x][j-y]就是

dp[i][j]中x長y寬的子矩陣的元素和（右下角元素為a[i][j]）

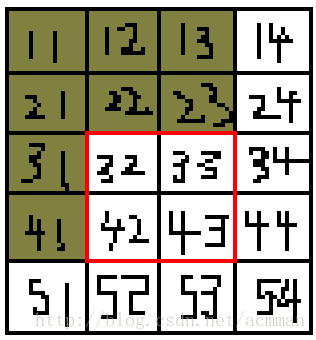
假設在a[5][4]矩陣中求dp[4][3]中長2寬2的子矩陣的元素和（僅僅求元素和，不是最大）

（我們只要求每次求出右下角的子矩陣即可，隨著矩陣擴大，答案就會被推算出來）

過程：

開始：

dp[4][3]代表的和

dp[4][1]代表的和

dp[2][3]代表的和

dp[2][1]代表的和

算出dp[4][3]中右下角長2寬2的子矩陣的元素和：

程式碼如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<algorithm>
using namespace std;
const int maxn=1005;

int dp[maxn][maxn];
int main()
{
    int i,j,n,m,T,x,y;
    scanf("%d",&T);
    while(T--)
    {
        int ans=0;
        scanf("%d%d%d%d",&m,&n,&x,&y);
        memset(dp,0,sizeof(dp));
        for(i=0; i<m; i++)
            for(j=0; j<n; j++)
            {
                scanf("%d",&dp[i][j]);
                dp[i][j]+=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1];
                if(i>=x-1&&j>=y-1)
                {
                    int maxx=dp[i][j]-dp[i][j-y]-dp[i-x][j]+dp[i-x][j-y];
                    ans=max(ans,maxx);
                }
            }
        printf("%d\n",ans);
    }
    return 0;
}