Stanford機器學習筆記-9. 聚類(Clustering)
9. Clustering
Content
9. Clustering
9.1 Supervised Learning and Unsupervised Learning
9.2 K-means algorithm
9.3 Optimization objective
9.4 Random Initialization
9.5 Choosing the Number of Clusters
9.1 Supervised Learning and Unsupervised Learning
我們已經學習了許多機器學習演算法,包括線性迴歸,Logistic迴歸,神經網路以及支援向量機。這些演算法都有一個共同點,即給出的訓練樣本自身帶有標記
![]()
顯然,現實生活中不是所有資料都帶有標記(或者說標記是未知的)。所以我們需要對無標記的訓練樣本進行學習,來揭示資料的內在性質及規律。我們把這種學習稱為無監督學習(Unsupervised Learning)
![]()
圖9-1形象的表示了監督學習與無監督學習的區別。圖(1)表示給帶標記的樣本進行分類,分界線兩邊為不同的類(一類為圈,另一類為叉);圖(2)是基於變數x1和x2對無標記的樣本(表面上看起來都是圈)進行聚類(Clustering)。
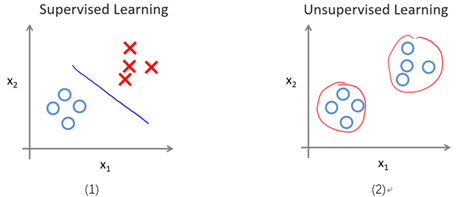
圖9-1 一個監督學習與無監督學習的區別例項
無監督學習也有很多應用,一個聚類的例子是:對於收集到的論文,根據每個論文的特徵量如詞頻,句子長,頁數等進行分組。聚類還有許多其它應用,如圖9-2所示。一個非聚類的例子是雞尾酒會演算法,即從帶有噪音的資料中找到有效資料(資訊),例如在嘈雜的雞尾酒會你仍然可以注意到有人叫你。所以雞尾酒會演算法可以用於語音識別(詳見
quora上有更多關於監督學習與無監督學習之間的區別的討論。
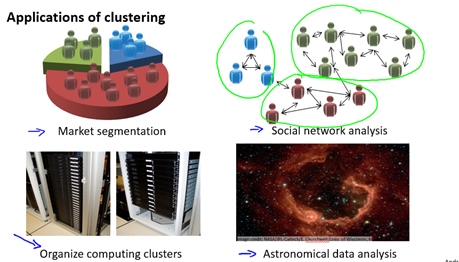
圖9-2 一些聚類的應用
9.2 K-means algorithm
聚類的基本思想是將資料集中的樣本劃分為若干個通常是不相交的子集,每個子集稱為一個"簇"(cluster)。劃分後,每個簇可能有對應的概念(性質),比如根據頁數,句長等特徵量給論文做簇數為2的聚類,可能得到一個大部分是包含碩士畢業論文的簇,另一個大部分是包含學士畢業論文的簇。
K均值(K-means)演算法是一個廣泛使用的用於簇劃分的演算法。下面說明K均值演算法的步驟:
- 隨機初始化K個樣本(點),稱之為簇中心(cluster centroids);
- 簇分配: 對於所有的樣本,將其分配給離它最近的簇中心;
- 移動簇中心:對於每一個簇,計算屬於該簇的所有樣本的平均值,移動簇中心到平均值處;
- 重複步驟2和3,直到找到我們想要的簇(即優化目標,詳解下節9.3)
圖9-3演示了以特徵量個數和簇數K均為2的情況。
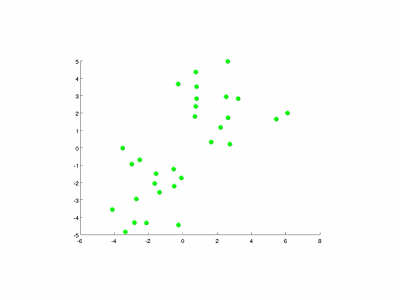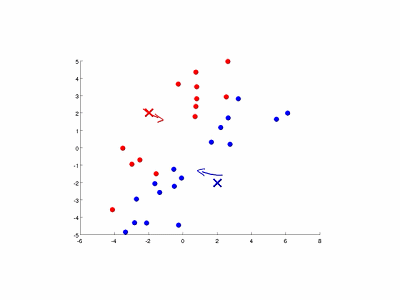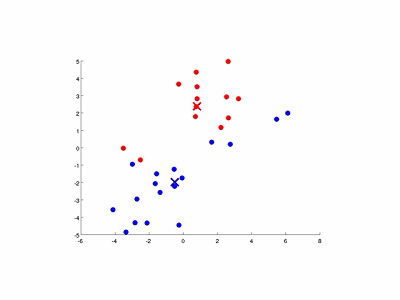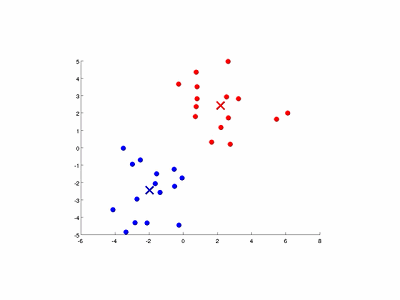
圖9-3 K均值演算法的演示
通過上述描述,下面我們形式化K均值演算法。
輸入:
- K (number of clusters)
-
Training set
 , where
, where 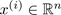 (drop
(drop 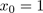 convention)
convention)
演算法:
Randomly initialize K cluster centroids
Repeat {
for i = 1 to m
:= index (from 1 to K ) of cluster centroid closest to
for k = 1 to K
:= average (mean) of points assigned to cluster
}
上述演算法中,第一個迴圈對應了簇分配的步驟:我們構造向量c,使得c(i)的值等於x(i)所屬簇的索引,即離x(i)最近簇中心的索引。用數學的方式表示如下:
![]()
第二個迴圈對應移動簇中心的步驟,即移動簇中心到該簇的平均值處。更數學的方式表示如下:
![]()
其中![]() 都是被分配給簇
都是被分配給簇 的樣本。
的樣本。
如果有一個簇中心沒有分配到一個樣本,我們既可以重新初始化這個簇中心,也可以直接將其去除。
經過若干次迭代後,該演算法將會收斂,也就是繼續迭代不會再影響簇的情況。
在某些應用中,樣本可能比較連續,看起來沒有明顯的簇劃分,但是我們還是可以用K均值演算法將樣本分為K個子集供參考。例如根據人的身高和體重劃分T恤的大小碼,如圖9-4所示。
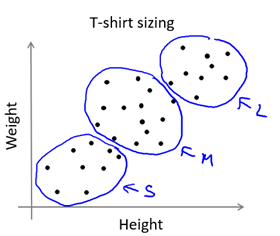
圖9-4 K-means for non-separated clusters
9.3 Optimization objective
重新描述在K均值演算法中使用的變數:
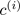 = index of cluster (1,2,…, K ) to which example
= index of cluster (1,2,…, K ) to which example 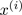 is currently assigned
is currently assigned
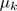 = cluster centroid k (
= cluster centroid k ( )
)
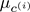 = cluster centroid of cluster to which example
= cluster centroid of cluster to which example 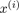 has been assigned
has been assigned
使用這些變數,定義我們的cost function如下: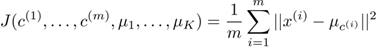
所以我們的優化目標就是
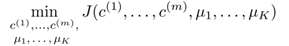
結合9.2節所描述的演算法,可以發現:
- 在簇分配步驟中,我們的目標是通過改變
 最小化J函式(固定
最小化J函式(固定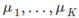 )
)
- 在移動簇中心步驟中,我們的目標通過改變
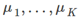 最小化J函式(固定
最小化J函式(固定 )
)
注意,在K均值演算法中,cost function不可能能增加,它應該總是下降的(區別於梯度下降法)。
9.4 Random Initialization
下面介紹一種值得推薦的初始化簇中心的方法。
- 確保K < m,也就是確保簇的數量應該小於樣本數;
- 隨機選擇K個訓練樣本;
-
令K個簇中心
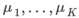 等於K個訓練樣本。
等於K個訓練樣本。
K均值演算法可能陷入區域性最優。為了減少這種情況的發生,我們可以基於隨機初始化,多次執行K均值演算法。所以,演算法變成如下形式(以執行100次為例:效率與準確性的tradeoff)
For i = 1 to 100 {
Randomly initialize K-means.
Run K-means. Get
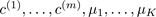
Compute cost function (distortion)
}
Pick clustering that gave lowest cost
9.5 Choosing the Number of Clusters
選擇K的取值通常是主觀的,不明確的。也就是沒有一種方式確保K的某個取值一定優於其他取值。但是,有一些方法可供參考。
The elbow method : 畫出代價J關於簇數K的函式圖,J值應該隨著K的增加而減小,然後趨於平緩,選擇當J開始趨於平衡時的K的取值。如圖9-5的(1)所示。
但是,通常這條曲線是漸變的,沒有很顯然的"肘部"。如圖9-5的(2)所示。
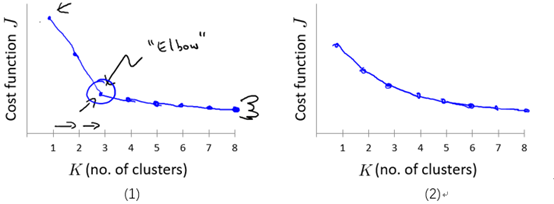
圖9-5 代價J關於簇數K的曲線圖
注意:隨著K的增加J應該總是減少的,否則,一種出錯情況可能是K均值陷入了一個糟糕的區域性最優。
當然,我們有時應該根據後續目的( later/downstream purpose )來確定K的取值。還是以根據人的身高和體重劃分T恤的大小碼為例,若我們想將T恤大小劃分為S/M/L這3種類型,那麼K的取值應為3;若想要劃分為XS/S/M/L/XL這5種類型,那麼K的取值應為5。如圖9-6所示。
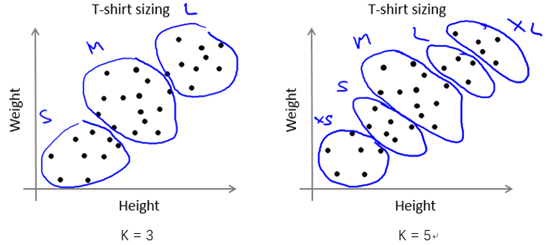
圖9-6 劃分T恤size的兩種不同情況