文章《You Only Look Once: Unified, Real-Time Object Detection》提出方法下面簡稱YOLO。

目前，基於深度學習演算法的一系列目標檢測演算法大致可以分為兩大流派：
1.兩步走（two-stage）演算法：先產生候選區域然後再進行CNN分類(RCNN系列)，
2.一步走（one-stage）演算法：直接對輸入影象應用演算法並輸出類別和相應的定位(YOLO系列)

之前的R-CNN系列雖然準確率比較高，但是即使是發展到Faster R-CNN，檢測一張圖片如下圖所示也要7fps(原文為5fps)，為了使得檢測的工作能夠用到實時的場景中，提出了YOLO。

YOLO的檢測思想不同於R-CNN系列的思想，它將目標檢測作為迴歸任務來解決。
下面來看看YOLO的整體結構：

由上兩圖所示，網路是根據GoogLeNet改進的，輸入圖片為448*448大小，輸出為 7×7×(2×5+20) $7\times 7\times$

( 2 × 5 + 20 ) $7\times7\times(2\times5+20)$，現在看來這樣寫輸出維度很奇怪，下面來看一下輸出是怎麼定義的。

將圖片分為 S×S $S$

× S $S\times S$個單元格(原文中S=7)，之後的輸出是以單元格為單位進行的：
1.如果一個object的中心落在某個單元格上，那麼這個單元格負責預測這個物體。
2.每個單元格需要預測B個bbox值(bbox值包括座標和寬高，原文中B=2)，同時為每個bbox值預測一個置信度(confidence scores)。也就是每個單元格需要預測B×(4+1)個值。
3.每個單元格需要預測C(物體種類個數，原文C=20，這個與使用的資料庫有關)個條件概率值.
所以，最後網路的輸出維度為$S \times S \times (B\times 5 + C)$，這裡雖然每個單元格負責預測一種物體(這也是這篇文章的問題，當有小物體時可能會有問題)，但是每個單元格可以預測多個bbox值(這裡可以認為有多個不同形狀的bbox，為了更準確的定位出物體，如下圖所示)。

因為這裡是當作迴歸問題來解決的，所以所有的輸出包括座標和寬高最好都定義在0到1之間。網上看見一張比較詳細的圖如下。

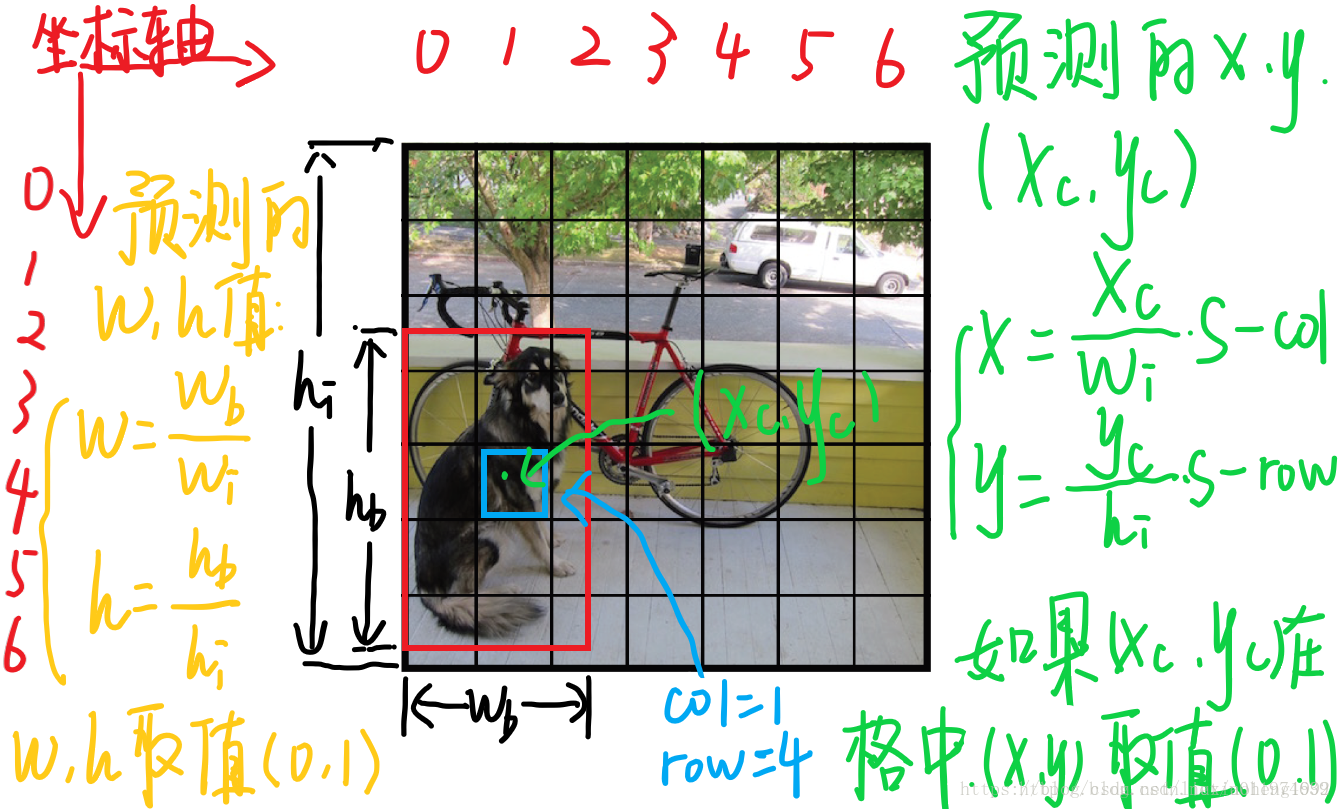
來看一下每個單元格預測的B個(x,y,w,h,confidence)的向量和C的條件概率中，每個引數的含義(假設圖片寬為{w_i}高為{hi}，將圖片分為$S\times S$)：
1.(x,y)是bbox的中心相對於單元格的offset
對於下圖中藍色框的那個單元格(座標為$(x_{col}=1,y_{row}=4)$)，假設它預測的輸出是紅色框的bbox,設bbox的中心座標為$(x_c,y_c)$,那麼最終預測出來的(x,y)是經過歸一化處理的，表示的是中心相對於單元格的offset，計算公式如下：
$x=\frac{x_c}{w_i}{S}−x_{col} , y=\frac{y_c}{h_i}{S}−y_{row}$

2.(w,h)是bbox相對於整個圖片的比例
預測的bbox的寬高為$w_b,h_b$，(w,h)表示的是bbox的是相對於整張圖片的佔比，計算公式如下:
$w=\frac{w_b}{w_i} , h=\frac{h_b}{h_i}$

3.confidence
這個置信度是由兩部分組成，一是格子內是否有目標，二是bbox的準確度。定義置信度為$P_r(Object)∗IOU^{truth}_{pred}$。
這裡，如果格子內有物體，則$P_r(Object)=1$，此時置信度等於IoU。如果格子內沒有物體，則$P_r(Object)=0$，此時置信度為0

4.C類的條件概率
條件概率定義為$P_r(Class_i |Object)$，表示該單元格存在物體且屬於第i類的概率。

在測試的時候每個單元格預測最終輸出的概率定義為，如下兩圖所示（兩幅圖不一樣，代表一個框會輸出B列概率值）
$P_r(Class_i|Object) ∗ P_r(Object) ∗ IOU^{truth}_{pred} = P_r(Class_i) ∗ IOU^{truth}_{pred}$

最後將 $(S\times S)\times B\times20$ 列的結果送入NMS，最後即可得到最終的輸出框結果

最後來看一下訓練YOLO使用的損失函式定義(本想自己用latex打的，後來有個符號一直打不出來，使用網友的圖如下)

這裡強調兩點：
1.每個圖片的每個單元格不一定都包含object，如果沒有object，那麼confidence就會變成0，這樣在優化模型的時候可能會讓梯度跨越太大，模型不穩定跑飛了。為了平衡這一點，在損失函式中，設定兩個引數$λ_{corrd}$和$λ_{noobj}$，其中 λ

相關推薦

YOLO文章詳細解讀

文章《You Only Look Once: Unified, Real-Time Object Detection》提出方法下面簡稱YOLO。 目前，基於深度學習演算法的一系列目標檢測演算法大致可以分為兩大流派： 1.兩步走（two-stage）演算法：先產生候選區域然後再進行CNN

Faster R-CNN文章詳細解讀

文章《Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks》是為了改進Fast R-CNN而提出來的。因為在Fast R-CNN文章中的測試時間是不包括search selective時間

Fast R-CNN文章詳細解讀

文章《Fast R-CNN》，是在SPP-net的基礎上對R-CNN的再次改造。 關於R-CNN的細節請檢視R-CNN文章詳細解讀，關於SPP-net的細節請檢視SPP-net文章詳細解讀 先來回顧一下R-CNN和SPP-net的缺點： 1.R-CNN的缺點 訓練分為多個

SPP-net文章詳細解讀

文章《Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition》是在RCNN之後，是對RCNN的改進(關於RCNN可以檢視R-CNN文章詳細解讀)，先給出SPP-net總的框架圖如下

R-CNN文章詳細解讀

這是13年的文章《Rich feature hierarchies for accurate object detection and semantic segmentation》，網上雖然很多文章寫過，但是有些很亂，有些不詳細，自己也花了不少時間看原文和各種部落格，想寫篇詳細的自己記錄下並

結繩法：文章詳細解讀（非同步時鐘設計的同步策略）（五）

一.典型方法（雙鎖存器法）    典型方法即雙鎖存器法，第一個鎖存器可能出現亞穩態，但是第二個鎖存器出現亞穩態的機率已經降到非常小，雙鎖存器雖然不能完全根除亞穩態的出現(事實上所有電路都無法根除，只能儘可能降低亞穩態的出現)，但是基本能夠在很大程度上減小這種機率

圖解集合7：紅黑樹概念、紅黑樹的插入及旋轉操作詳細解讀

集合 得到 2個 排序。 數據流 except boolean 修正 split 原文地址http://www.cnblogs.com/xrq730/p/6867924.html，轉載請註明出處，謝謝！ 初識TreeMap 之前的文章講解了兩種Map，分別是HashMa

MySql之ALTER命令用法詳細解讀（轉）

修改表 pre const 命令使用 add ear 修改 blog rain 本文詳細解讀了MySql語法中Alter命令的用法，這是一個用法比較多的語法，而且功能還是很強大的。 USE learning;(自己要提前建好) CREATE TABLE student

JMX超詳細解讀

唯一標識 命名 mode 架構 iter invoke 應用場景 elm span 一、JMX的定義　　 　　JMX(Java Management Extensions)是一個為應用程序植入管理功能的框架。JMX是一套標準的代理和服務，實際上，用戶可以在任何Java應用程

詳細解讀-this-關鍵字在全局、函數、對象、jQuery中的基礎用法！

瀏覽器中 person ack true ++ 例子 span mar 編程 一、前言 1、 Javascript是一門基於對象的動態語言，也就是說，所有東西都是對象，一個很典型的例子就是函數也被視為普通的對象。Javascript可以通過一定的設計模式來實現面向對

詳細解讀Jquery各Ajax函數：$.get(),$.post(),$.ajax(),$.getJSON()

type value 簡便 幫助 map last 滿足 處理 精確 一，$.get(url,[data],[callback]) 說明：url為請求地址，data為請求數據的列表(是可選的，也可以將要傳的參數寫在url裏面)，callback為請求成功後的回調函數，

Jquery的$.get(),$.post(),$.ajax(),$.getJSON()用法詳細解讀

ajax 希望 得到 請求 字符串 說明 blog start 添加 1、$.get $.get()方法使用GET方式來進行異步請求，它的語法結構為： $.get( url [, data] [, callback] ) 解釋一下這個函數的各個參數： url：string類

const類型變量的詳細解讀

指針 地址 不可 錯誤 div log 變量 tro 類型 const類型變量--------------------------------------int i;const int *p; --------------------------------------in

Linux中軟鏈接與硬鏈接詳細解讀

正常 -a ext 驗證 觀察 imp file border ali 目標：1.測試環境模擬2.軟鏈接特性3.硬鏈接特性4.總結1.測試環境模擬12345678910111213[root@localhost home]# mkdir test 創建測試文件夾[root@

分享點幹貨（此this非彼this）this的詳細解讀

使用 編程 var pan his () col 作者 分析 在javascript編程中，this關鍵字經常讓初學者感到迷惑，這裏，針對此this根據查閱的資料和個人的理解分享一下，純手打，大神勿噴。 首先先說一下this的指向，大致可以分為以下四種。 1.作為對象的方法

VINS-mono詳細解讀

fusion 尋找 結果 field 錯誤 記錄 不用 tomat IE VINS-mono詳細解讀 極品巧克力 前言 Vins-mono是香港科技大學開源的一個VIO算法，https://github.com/HKUST-Aerial-Robotics/VINS-Mo

相機IMU融合四部曲（二）：誤差狀態四元數詳細解讀

center 討論 組合 計算 運算 white 成了 mes 操作 相機IMU融合四部曲（二）：誤差狀態四元數詳細解讀 極品巧克力 前言 上一篇文章，《D-LG-EKF詳細解讀》中，講了理論上的SE3上相機和IMU融合的思想。但是，還沒有涉及到實際的操作，以及實際操作

[文文殿下]並查集詳細解讀

學習 應該 論文 一點 mar 訪問 單純 pic 官方 初探並查集 並查集(Disjoint-Set)是一種優美的數據結構，它擅長動態維護若幹交集為空的集合，並且支持快速合並兩個集合以及查找某個元素所在的集合。 然而這只是並查集所能做的一點微小的工作，文文對並查集的理解是

C4.5最新版本Release8與ＭＤＬ的關係的詳細解讀

最近聯絡了決策樹的作者Ｑｕｉｎｌａｎ教授，搞清了網上對Ｃ４．５的一些不夠前沿的描述， 《Inferring Decision Trees Using the Minimum Description Length Principle*》 《Improved Use of Continuou

HTML+CSS第五課：使用Dreamweaver工具製作網頁、詳細解讀HTML頭部標籤、網頁頭部標籤的SEO設定

知識點：Dreamweaver工具的使用、HTML頭部標籤解讀、網頁頭部標籤的SEO設定 1、Dreamweaver工具            Adobe Dreamweaver，簡稱“DW”，中文名稱 "夢想編織者"，最初為美