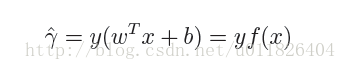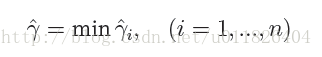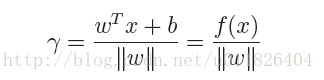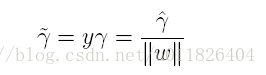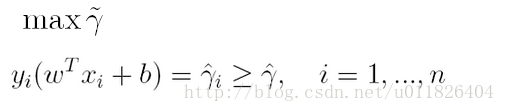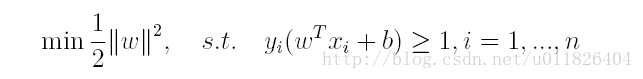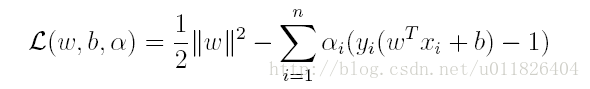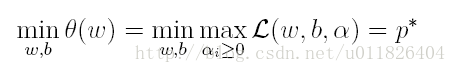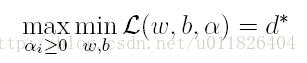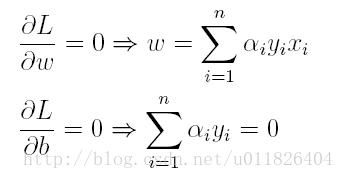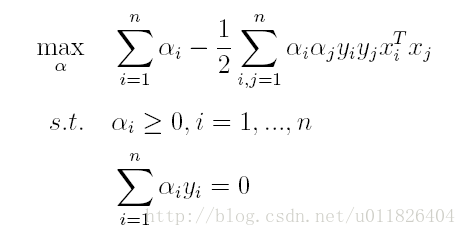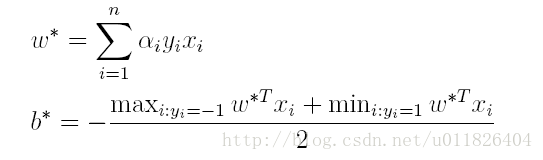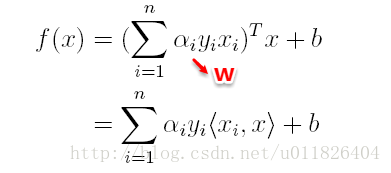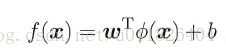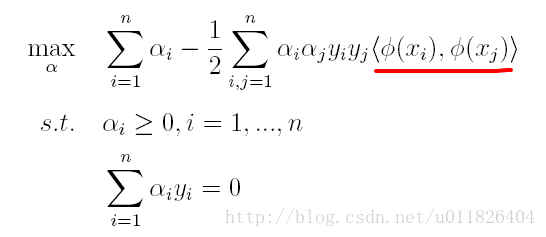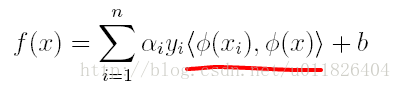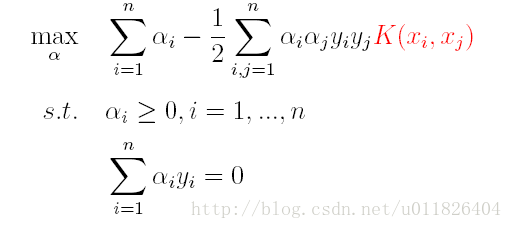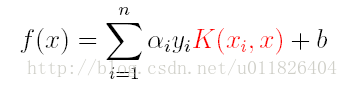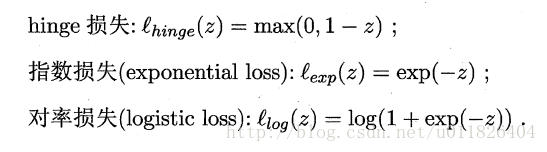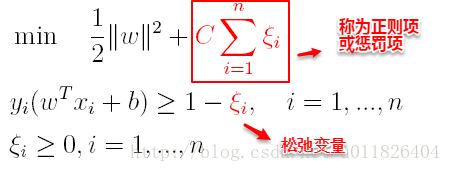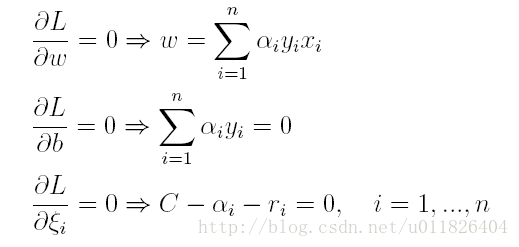寫在前面的話：距離上篇部落格竟過去快一個月了，寫完神經網路部落格正式進入考試模式，幾次考試+幾篇報告下來弄得心頗不寧靜了，今日定下來看到一句雞血：Tomorrow is another due！也許生活就需要一些deadline~~

上篇主要介紹了神經網路。首先從生物學神經元出發，引出了它的數學抽象模型–MP神經元以及由兩層神經元組成的感知機模型，並基於梯度下降的方法描述了感知機模型的權值調整規則。由於簡單的感知機不能處理線性不可分的情形，因此接著引入了含隱層的前饋型神經網路，BP神經網路則是其中最為成功的一種學習方法，它使用誤差逆傳播的方法來逐層調節連線權。最後簡單介紹了局部/全域性最小以及目前十分火熱的深度學習的概念。本篇圍繞的核心則是曾經一度取代過神經網路的另一種監督學習演算法–支援向量機

6、支援向量機

支援向量機是一種經典的二分類模型，基本模型定義為特徵空間中最大間隔的線性分類器，其學習的優化目標便是間隔最大化，因此支援向量機本身可以轉化為一個凸二次規劃求解的問題。

6.1 函式間隔與幾何間隔

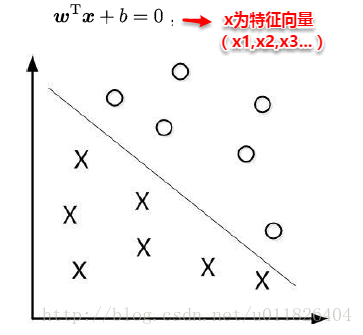
對於二分類學習，假設現在的資料是線性可分的，這時分類學習最基本的想法就是找到一個合適的超平面，該超平面能夠將不同類別的樣本分開，類似二維平面使用ax+by+c=0來表示，超平面實際上表示的就是高維的平面，如下圖所示：

對資料點進行劃分時，易知：當超平面距離與它最近的資料點的間隔越大，分類的魯棒性越好，即當新的資料點加入時，超平面對這些點的適應性最強，出錯的可能性最小。因此需要讓所選擇的超平面能夠最大化這個間隔Gap（如下圖所示）， 常用的間隔定義有兩種，一種稱之為函式間隔，一種為幾何間隔，下面將分別介紹這兩種間隔，並對SVM為什麼會選用幾何間隔做了一些闡述。

6.1.1 函式間隔

在超平面w’x+b=0確定的情況下，|w’x*+b|能夠代表點x*距離超平面的遠近，易知：當w’x*+b>0時，表示x*在超平面的一側（正類，類標為1），而當w’x*+b<0時，則表示x*在超平面的另外一側（負類，類別為-1），因此（w’x*+b）y* 的正負性恰能表示資料點x*是否被分類正確。於是便引出了函式間隔的定義（functional margin）:

而超平面（w,b）關於所有樣本點（Xi，Yi）的函式間隔最小值則為超平面在訓練資料集T上的函式間隔：

可以看出：這樣定義的函式間隔在處理SVM上會有問題，當超平面的兩個引數w和b同比例改變時，函式間隔也會跟著改變，但是實際上超平面還是原來的超平面，並沒有變化。例如：w1x1+w2x2+w3x3+b=0其實等價於2w1x1+2w2x2+2w3x3+2b=0，但計算的函式間隔卻翻了一倍。從而引出了能真正度量點到超平面距離的概念–幾何間隔（geometrical margin）。

6.1.2 幾何間隔

幾何間隔代表的則是資料點到超平面的真實距離，對於超平面w’x+b=0，w代表的是該超平面的法向量，設x*為超平面外一點x在法向量w方向上的投影點，x與超平面的距離為r，則有x*=x-r(w/||w||)，又x*在超平面上，即w’x*+b=0，代入即可得：

為了得到r的絕對值，令r呈上其對應的類別y，即可得到幾何間隔的定義：

從上述函式間隔與幾何間隔的定義可以看出：實質上函式間隔就是|w’x+b|，而幾何間隔就是點到超平面的距離。

6.2 最大間隔與支援向量

通過前面的分析可知：函式間隔不適合用來最大化間隔，因此這裡我們要找的最大間隔指的是幾何間隔，於是最大間隔分類器的目標函式定義為：

一般地，我們令r^為1（這樣做的目的是為了方便推導和目標函式的優化），從而上述目標函式轉化為：

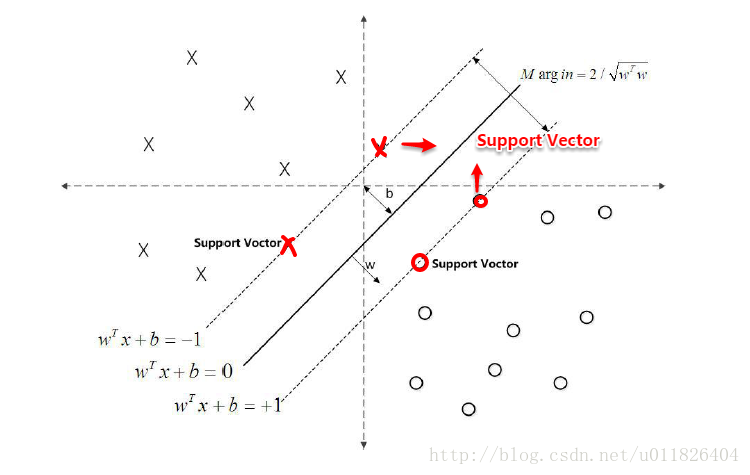
對於y(w’x+b)=1的資料點，即下圖中位於w’x+b=1或w’x+b=-1上的資料點，我們稱之為支援向量（support vector），易知：對於所有的支援向量，它們恰好滿足y*(w’x*+b)=1，而所有不是支援向量的點，有y*(w’x*+b)>1。

6.3 從原始優化問題到對偶問題

對於上述得到的目標函式，求1/||w||的最大值相當於求||w||^2的最小值，因此很容易將原來的目標函式轉化為：

即變為了一個帶約束的凸二次規劃問題，按書上所說可以使用現成的優化計算包（QP優化包）求解，但由於SVM的特殊性，一般我們將原問題變換為它的對偶問題，接著再對其對偶問題進行求解。為什麼通過對偶問題進行求解，有下面兩個原因：

* 一是因為使用對偶問題更容易求解；
* 二是因為通過對偶問題求解出現了向量內積的形式，從而能更加自然地引出核函式。

對偶問題，顧名思義，可以理解成優化等價的問題，更一般地，是將一個原始目標函式的最小化轉化為它的對偶函式最大化的問題。對於當前的優化問題，首先我們寫出它的朗格朗日函式：

上式很容易驗證：當其中有一個約束條件不滿足時，L的最大值為 ∞（只需令其對應的α為 ∞即可）；當所有約束條件都滿足時，L的最大值為1/2||w||^2（此時令所有的α為0），因此實際上原問題等價於：

由於這個的求解問題不好做，因此一般我們將最小和最大的位置交換一下（需滿足KKT條件） ，變成原問題的對偶問題：

這樣就將原問題的求最小變成了對偶問題求最大（用對偶這個詞還是很形象），接下來便可以先求L對w和b的極小，再求L對α的極大。

（1）首先求L對w和b的極小，分別求L關於w和b的偏導，可以得出：

將上述結果代入L得到：

（2）接著L關於α極大求解α（通過SMO演算法求解，此處不做深入）。

（3）最後便可以根據求解出的α，計算出w和b，從而得到分類超平面函式。

在對新的點進行預測時，實際上就是將資料點x*代入分類函式f(x)=w’x+b中，若f(x)>0，則為正類，f(x)<0，則為負類，根據前面推導得出的w與b，分類函式如下所示，此時便出現了上面所提到的內積形式。

這裡實際上只需計算新樣本與支援向量的內積，因為對於非支援向量的資料點，其對應的拉格朗日乘子一定為0，根據最優化理論（K-T條件），對於不等式約束y(w’x+b)-1≥0，滿足：

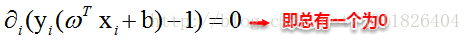
6.4 核函式

由於上述的超平面只能解決線性可分的問題，對於線性不可分的問題，例如：異或問題，我們需要使用核函式將其進行推廣。一般地，解決線性不可分問題時，常常採用對映的方式，將低維原始空間對映到高維特徵空間，使得資料集在高維空間中變得線性可分，從而再使用線性學習器分類。如果原始空間為有限維，即屬性數有限，那麼總是存在一個高維特徵空間使得樣本線性可分。若∅代表一個對映，則在特徵空間中的劃分函式變為：

按照同樣的方法，先寫出新目標函式的拉格朗日函式，接著寫出其對偶問題，求L關於w和b的極大，最後運用SOM求解α。可以得出：

（1）原對偶問題變為：

（2）原分類函式變為：

求解的過程中，只涉及到了高維特徵空間中的內積運算，由於特徵空間的維數可能會非常大，例如：若原始空間為二維，對映後的特徵空間為5維，若原始空間為三維，對映後的特徵空間將是19維，之後甚至可能出現無窮維，根本無法進行內積運算了，此時便引出了核函式（Kernel）的概念。

因此，核函式可以直接計算隱式對映到高維特徵空間後的向量內積，而不需要顯式地寫出對映後的結果，它雖然完成了將特徵從低維到高維的轉換，但最終卻是在低維空間中完成向量內積計算，與高維特徵空間中的計算等效（低維計算，高維表現），從而避免了直接在高維空間無法計算的問題。引入核函式後，原來的對偶問題與分類函式則變為：

（1）對偶問題：

（2）分類函式：

因此，線上性不可分問題中，核函式的選擇成了支援向量機的最大變數，若選擇了不合適的核函式，則意味著將樣本對映到了一個不合適的特徵空間，則極可能導致效能不佳。同時，核函式需要滿足以下這個必要條件：

由於核函式的構造十分困難，通常我們都是從一些常用的核函式中選擇，下面列出了幾種常用的核函式：

6.5 軟間隔支援向量機

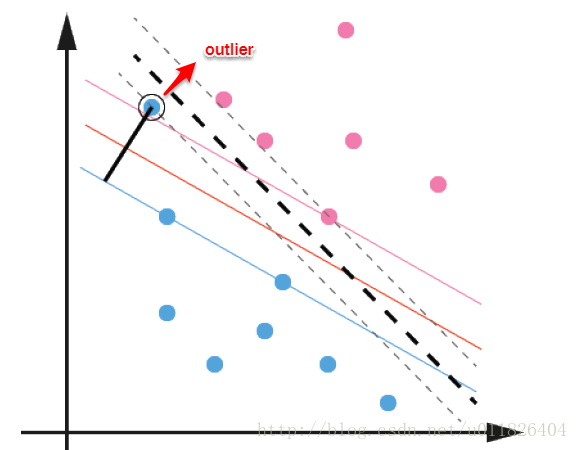
前面的討論中，我們主要解決了兩個問題：當資料線性可分時，直接使用最大間隔的超平面劃分；當資料線性不可分時，則通過核函式將資料對映到高維特徵空間，使之線性可分。然而在現實問題中，對於某些情形還是很難處理，例如資料中有噪聲的情形，噪聲資料（outlier）本身就偏離了正常位置，但是在前面的SVM模型中，我們要求所有的樣本資料都必須滿足約束，如果不要這些噪聲資料還好，當加入這些outlier後導致劃分超平面被擠歪了，如下圖所示，對支援向量機的泛化效能造成很大的影響。

為了解決這一問題，我們需要允許某一些資料點不滿足約束，即可以在一定程度上偏移超平面，同時使得不滿足約束的資料點儘可能少，這便引出了“軟間隔”支援向量機的概念

* 允許某些資料點不滿足約束y(w'x+b)≥1；
* 同時又使得不滿足約束的樣本儘可能少。

這樣優化目標變為：

如同階躍函式，0/1損失函式雖然表示效果最好，但是數學性質不佳。因此常用其它函式作為“替代損失函式”。

支援向量機中的損失函式為hinge損失，引入“鬆弛變數”，目標函式與約束條件可以寫為：

其中C為一個引數，控制著目標函式與新引入正則項之間的權重，這樣顯然每個樣本資料都有一個對應的鬆弛變數，用以表示該樣本不滿足約束的程度，將新的目標函式轉化為拉格朗日函式得到：

按照與之前相同的方法，先讓L求關於w，b以及鬆弛變數的極小，再使用SMO求出α，有：

將w代入L化簡，便得到其對偶問題：

將“軟間隔”下產生的對偶問題與原對偶問題對比可以發現：新的對偶問題只是約束條件中的α多出了一個上限C，其它的完全相同，因此在引入核函式處理線性不可分問題時，便能使用與“硬間隔”支援向量機完全相同的方法。

—-在此SVM就介紹完畢。