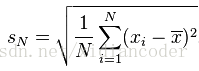平均值(Mean)、方差(Variance)、標準差(Standard Deviation)
本文目錄
開篇明志
對於一維資料的分析,最常見的就是計算平均值(Mean)、方差(Variance)和標準差(Standard Deviation)。在做【特徵工程】的時候,會出現缺失值,那麼經常會用到使用 平均值 或者 中位數等進行填充。
平均值
平均值的概念很簡單:所有資料之和除以資料點的個數,以此表示資料集的平均大小;其數學定義為
以下面10個點的CPU使用率資料為例,其平均值為17.2。
14 31 16 19 26 14 14 14 11 13方差、標準差
方差這一概念的目的是為了表示資料集中資料點的離散程度;其數學定義為:
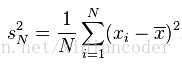
標準差與方差一樣,表示的也是資料點的離散程度;其在數學上定義為方差的平方根:
為什麼使用標準差?
與方差相比,使用標準差來表示資料點的離散程度有3個好處:
- 表示離散程度的數字與樣本資料點的數量級一致,更適合對資料樣本形成感性認知。依然以上述10個點的CPU使用率資料為例,其方差約為41,而標準差則為6.4;兩者相比較,標準差更適合人理解。
- 表示離散程度的數字單位與樣本資料的單位一致,更方便做後續的分析運算。
- 在樣本資料大致符合正態分佈的情況下,標準差具有方便估算的特性:66.7%的資料點落在平均值前後1個標準差的範圍內、95%的資料點落在平均值前後2個標準差的範圍內,而99%的資料點將會落在平均值前後3個標準差的範圍內。
貝賽爾修正
在上面的方差公式和標準差公式中,存在一個值為N的分母,其作用為將計算得到的累積偏差進行平均,從而消除資料集大小對計算資料離散程度所產生的影響。不過,使用N所計算得到的方差及標準差只能用來表示該資料集本身(population)的離散程度;如果資料集是某個更大的研究物件的樣本(sample),那麼在計算該研究物件的離散程度時,就需要對上述方差公式和標準差公式進行貝塞爾修正,將N替換為N-1:
經過貝塞爾修正後的方差公式:
經過貝塞爾修正後的標準差公式:
公式的選擇
是否使用貝塞爾修正,是由資料集的性質來決定的:如果只想計算資料集本身的離散程度(population),那麼就使用未經修正的公式;如果資料集是一個樣本(sample),而想要計算的則是樣本所表達物件的離散程度,那麼就使用貝塞爾修正後的公式。在特殊情況下,如果該資料集相較總體而言是一個極大的樣本 (比如一分鐘內採集了十萬次的IO資料) — 在這種情況下,該樣本資料集不可能錯過任何的異常值(outlier),此時可以使用未經修正的公式來計算總體資料的離散程度。
平均值與標準差的適用範圍及誤用
大多數統計學指標都有其適用範圍,平均值、方差和標準差也不例外,其適用的資料集必須滿足以下條件:
中部單峰:
資料集只存在一個峰值。很簡單,以假想的CPU使用率資料為例,如果50%的資料點位於20附近,另外50%的資料點位於80附近(兩個峰),那麼計算得到的平均值約為50,而標準差約為31;這兩個計算結果完全無法描述資料點的特徵,反而具有誤導性。
這個峰值必須大致位於資料集中部。還是以假想的CPU資料為例,如果80%的資料點位於20附近,剩下的20%資料隨機分佈於30~90之間,那麼計算得到的平均值約為35,而標準差約為25;與之前一樣,這兩個計算結果不僅無法描述資料特徵,反而會造成誤導。
遺憾的是,在現實生活中,很多資料分佈並不滿足上述兩個條件;因此,在使用平均值、方差和標準差的時候,必須謹慎小心。
如果資料集僅僅滿足一個條件:單峰。那麼,峰值在哪裡?峰的寬頻是多少?峰兩邊的資料對稱性如何?有沒有異常值(outlier)?為了回答這些問題,除了平均值、方差和標準差,需要更合適的工具和分析指標,而這,就是中位數、均方根、百分位數和四分差的意義所在。