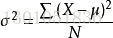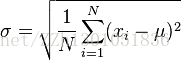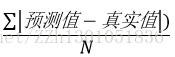單純介紹概念不易理解，所以應從實際應用出發介紹其區別。四者的不同可從研究物件和研究目的進行區分。

一 區別比較

1. 方差
   定義：方差在統計描述和概率分佈中各有不同的定義，並有不同的公式。
   （1）統計學
   統計學中的方差（樣本方差）是各個資料分別與其平均數之差的平方的和的平均數。
   （2）概率論
   度量隨機變數和其數學期望（即均值）之間的偏離程度。
   來源：
   離均差：即一個樣本中的資料與均值之差。將離均差進行改進得到了方差。
   。。。
   補充：
   離均差又是從極差發展而來的。
   極差是最大值－最小值，最初用極差來評價一組資料的離散度。
   因為由兩個資料來評判一組資料是不科學的，所以從極差進行改進，改用離均差之和。
   使用離均差不好嗎？為什麼又設定方差

   ：
   （1）為避免出現離均差總和為零，所以對離均差求平方。
   （2）而為避免離均差平方和受樣本含量的影響，所以對離均差平方和除以樣本數，求平均值。
   這樣就得到了方差。
   公式：
   （1）統計學
   針對總體資料的公式，其中N是總體資料的數量：
   
   為總體方差， 為變數， 為總體均值， 為總體資料數量。
   針對樣本抽樣的公式（日常工作中用）：
   S^2= ∑(X- ) ^2 / (n-1)
   實際工作中，總體均數難以得到時，應用樣本統計量（即樣本數量）代替總體引數，經校正後，樣本方差計算公式如上。除以n-1的原因見自由度（為什麼樣本方差自由度是n-1）_張之海_CSDN
   其中S^2為樣本方差，X為變數，為樣本均值，n為樣本例數。
   （2）概率論
   離散型隨機變數：
   D(X)=E{[X-E(X)]^2}=E(X
   2) - [ E(X)]^2
   連續型隨機變數：
   定義域為(a,b)，概率密度函式為f(x)，連續型隨機變數X方差計算公式：
   D(X)= (x-μ)^2 f(x) dx
   意義：
   當資料分佈比較分散（即資料在平均數附近波動較大）時，各個資料與平均數的差的平方和較大，方差就較大；當資料分佈比較集中時，各個資料與平均數的差的平方和較小。因此方差越大，資料的波動越大；方差越小，資料的波動就越小。

2. 標準差(std —— Standard Deviation)
   別名：均方差（mean square error）、標準偏差、實驗標準差。
   定義：標準差是觀測值與其平均數偏差的平方和的平方根，即方差的算術平方根。
   公式

   :
   
   公式意義：所有數減去其平均值的平方和，所得結果除以該組數之個數（或個數減一)，再把所得值開根號，所得之數就是這組資料的標準差。
   注意：如是總體，標準差公式根號內除以N。如是樣本，標準差公式根號內除以（N-1) 。因為我們大量接觸的是樣本，所以普遍使用根號內除以（N-1)。
   理論意義：
   （1）標準差反映組內個體間的離散程度。
   （2）描述一組數值自平均值分散開來的程度。一個較大的標準差，代表大部分的數值和其平均值之間差異較大；一個較小的標準差，代表這些數值較接近平均值。
   （3）標準差越高,表示實驗資料越離散,也就是說越不精確。標準差越低,代表實驗的資料越精確。
   實際應用：
   標準差應用於投資上，可作為量度回報穩定性的指標。標準差數值越大，代表回報遠離過去平均數值，回報較不穩定故風險越高。相反，標準差數值越細，代表回報較為穩定，風險亦較小。
   方差、標準差的關係與異同：
   （1）兩者的關係
   樣本中各資料與樣本平均數的差的平方和的平均數叫做樣本方差；樣本方差的算術平方根叫做樣本標準差。
   （2）相同點
   兩者都是描述一組（協方差描述兩組資料，參考[4]）資料的離散程度的。樣本方差或樣本標準差越大，樣本資料的離散程度就越大。
   （3）不同點
   方差與我們要處理的資料的量綱是不一致的，雖然能很好的描述資料與均值的偏離程度，但是處理結果是不符合我們的直觀思維的。
   標準差與方差不同的是，標準差和變數的計算單位相同，比方差清楚，因此很多時候我們分析的時候更多的使用的是標準差。
   標準差和均值的量綱（單位）是一致的，在描述一個波動範圍時標準差比方差更方便。比如一個班男生的平均身高是170cm,標準差是10cm,那麼方差就是10cm^2。可以進行的比較簡便的描述是本班男生身高分佈是170±10cm，方差就無法做到這點。

3. 協方差
   用途：衡量兩個變數的總體誤差。
   .
   與方差、標準差的不同：協方差表示的是兩個變數的總體的誤差，這與只表示一個變數誤差的方差不同。 如果兩個變數的變化趨勢一致，也就是說如果其中一個大於自身的期望值，另外一個也大於自身的期望值，那麼兩個變數之間的協方差就是正值。 如果兩個變數的變化趨勢相反，即其中一個大於自身的期望值，另外一個卻小於自身的期望值，那麼兩個變數之間的協方差就是負值。
   .
   公式：
   
   
   從公式中可以看出，協方差是各隨機變數與其均數離差之積的均值；如果我們把隨機變數與其均數的差值成為“均值化“的隨機變數，這麼這兩個均值化的隨機變數應該都具有相同的均值就是0；同時如果二者是相互獨立的，那麼當X大於其均值的情況下Y應該是有可能大於也有可能小於其均值，這樣導致其乘積之和應該為0；也就是說，如果X、Y相互獨立，則二者協方差為0。同樣可知，如果X、Y線性相關，則其一個大於均值的時候另一個也會大於均值的（因為其均值也是線性相關的）。於是可以看出協方差是判斷兩個隨機變數是否線性相關的很好的物理量。
   特殊情況：
   如果X與Y是統計獨立的，那麼二者之間的協方差就是0，因為兩個獨立的隨機變數滿足E[XY]=E[X]E[Y]。
   但是，反過來並不成立。即如果X與Y的協方差為0，二者並不一定是統計獨立的。（相關有兩種：線性相關、非線性相關。Cov(X,Y)等於0，說明X與Y一定不是線性相關，但是X與Y可能是非線性相關（eg:Y = X^2），這樣X與Y仍不是相互獨立的。）
   .
   協方差與期望、方差的關係：
   協方差與方差之間有如下關係：
   D(X+Y)=D(X)+D(Y)+2Cov(X，Y)
   D(X-Y)=D(X)+D(Y)-2Cov(X，Y)
   協方差與期望值有如下關係：
   Cov(X，Y)=E(XY)-E(X)E(Y)。
   .
   協方差與pearson係數的關係：
   協方差作為描述X和Y相關程度的量，在同一物理量綱之下有一定的作用，但同樣的兩個量採用不同的量綱使它們的協方差在數值上表現出很大的差異。因此才引入了Pearson相關係數。
   
   若ρXY=0，則X與Y不線性相關。
   即ρXY=0的充分必要條件是Cov(X，Y)=0，亦即不相關和協方差為零是等價的。
   設ρXY是隨機變數X和Y的相關係數，則有
   （1）∣ρXY∣≤1；
   （2）∣ρXY∣=1充分必要條件為P{Y=aX+b}=1，（a，b為常數，a≠0）

4. 均方根誤差(rmse —— root-mean-square error)
   別名:標準誤差、均方根差。
   定義：觀測值與真值偏差的平方和，與觀測次數n比值的平方根。
   公式：
   （1）表示1：√[∑(di^2)/n]
   （2）表示2：S={[(x1-x’1)^2+(x2-x’2)2+…(xn-x’n)^2]/n}0.5（x’1、x’2…x’n為真實值，n為樣本個數）
   理論意義：衡量觀測值同真值之間的偏差。
   實際用途：衡量測量精度。
   實際應用：標準誤差 對一組測量中的特大或特小誤差反映非常敏感，所以，標準誤差能夠很好地反映出測量的精密度。這正是標準誤差在工程測量中廣泛被採用的原因。

5. 平均絕對誤差(MAE)
   別名：平均絕對離差
   定義：所有單個觀測值與算術平均值的偏差，的絕對值，的平均。
   公式：
   理論意義：平均絕對誤差可以避免偏差相互抵消的問題。
   實際用途：描述資料離散程度。

二 離散度形容指標發展歷史

極差、方差和標準差等都是形容離散度的指標。
離散度
　　標準差是反應一組資料離散程度最常用的一種量化形式，是表示精密確的最要指標。說起標準差首先得搞清楚它出現的目的。我們使用方法去檢測它，但檢測方法總是有誤差的，所以檢測值並不是其真實值。檢測值與真實值之間的差距就是評價檢測方法最有決定性的指標。但是真實值是多少，不得而知。因此怎樣量化檢測方法的準確性就成了難題。這也是臨床工作質控的目的：保證每批實驗結果的準確可靠。 　　
　　雖然樣本的真實值是不可能知道的，但是每個樣本總是會有一個真實值的，不管它究竟是多少。可以想象，一個好的檢測方法，其檢測值應該很緊密的分散在真實值周圍。如果不緊密，那距真實值的就會大，準確性當然也就不好了，不可能想象離散度大的方法，會測出準確的結果。因此，離散度是評價方法的好壞的最重要也是最基本的指標。 　　
　　一組資料怎樣去評價和量化它的離散度呢?人們使用了很多種方法：
極差
　　最直接也是最簡單的方法，即最大值－最小值（也就是極差）來評價一組資料的離散度。這一方法在日常生活中最為常見，比如比賽中去掉最高最低分就是極差的具體應用。
離均差的平方和
　　由於誤差的不可控性，因此只由兩個資料來評判一組資料是不科學的。所以人們在要求更高的領域不使用極差來評判。其實，離散度就是資料偏離平均值的程度。因此將資料與均值之差（我們叫它離均差）加起來就能反映出一個準確的離散程度。和越大離散度也就越大。 　　但是由於偶然誤差是成正態分佈的，離均差有正有負，對於大樣本離均差的代數和為零的。為了避免正負問題，在數學有上有兩種方法：一種是取絕對值，也就是常說的離均差絕對值之和。而為了避免符號問題，數學上最常用的是另一種方法－－平方，這樣就都成了非負數。因此，離均差的平方和成了評價離散度一個指標。　　
方差（S2）
　　由於離均差的平方和與樣本個數有關，只能反應相同個數樣本的離散度，而實際工作中做比較很難做到樣本的個數相同，因此為了消除樣本個數的影響，增加可比性，將標準差求平均值，這就是我們所說的方差成了評價離散度的較好標準。 　　
　　樣本量越大越能反映真實的情況，而算數均值卻完全忽略了這個問題，對此統計學上早有考慮，在統計學中樣本的方差多是除以自由度（n-1)，它是意思是樣本能自由選擇的程度。當選到只剩一個時，它不可能再有自由了，所以自由度是n-1。為什麼除以n-1呢？請參考：自由度（為什麼樣本方差自由度是n-1）_張之海_CSDN