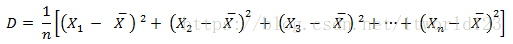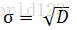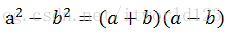方差、標準差、平方差、殘差
2018-06-21 建立人:Ruo_Xiao
郵箱:[email protected]
2018-06-29 修改人:Ruo_Xiao
增加對殘差的說明。
一、方差
1、定義:資料分別與其平均數的差的平方和的平均數,由“D”表示。
2、意義:用於度量隨機變數與數學期望(即均值)之間的偏離程度。
3、公式如下:
二、標準差
- 又名:均方差,用“σ”表示。
- 公式如下:
三、平方差
四、殘差
- 在實際數理統計中,觀測值和估計值(擬合值)之間的差。
- 栗子:二維空間中,10個點擬合出一條直線方程,其中一個點的座標為(X,Y),將該點的X代入
擬合得到的方程中,得到擬合值為Y0,則殘差為Y - Y0. - 反應的是資料的離散程度以及收斂性,越大則資料離散程度越大、越不收斂。
(SAW:Game Over!)
相關推薦
各種距離 歐式距離、曼哈頓距離、切比雪夫距離、閔可夫斯基距離、標準歐氏距離、馬氏距離、余弦距離、漢明距離、傑拉德距離、相關距離、信息熵
form 密碼學 一行 and gif 國際象棋 matlab 三維空間 ffi 1. 歐氏距離(Euclidean Distance) 歐氏距離是最容易直觀理解的距離度量方法,我們小學、初中和高中接觸到的兩個點在空間中的距離一般都是指歐氏距離。 二維平面上點a(x1,
javaSE (三十三)其他流(序列流、記憶體輸出流、隨機訪問流、物件操作流、資料輸入輸出流、列印流、標準輸入輸出流、properties)
1、序列流(SequenceInputStream ): 序列流主要的作用就是整合位元組輸入流,將很多的進口整合成一個 這裡著重講一下多於兩個輸入流的整合: 步驟: 建立三個輸入流 建立vector集合存入這些輸入流 將這些輸入流變成列舉型別 Vector.e
【機器學習】【線性代數】正交基、標準正交基、正交矩陣,正交變換等數學知識點
1.正交向量組直接給定義:歐式空間V的一組非零向量,如果他們倆倆向量正交,則稱是一個正交向量組。(1)正交向量組 是 線性無關的(2)n維歐式空間中倆倆正交的非零向量不會超過n個,即n維歐式空間中一個正交向量組最多n個向量2.正交基在n維歐式空間中,由n個非零向量組成的正交向
方差、標準差、平方差、殘差
2018-06-21 建立人:Ruo_Xiao 郵箱:[email protected] 2018-06-29 修改人:Ruo_Xiao 增加對殘差的說明。 一、方差 1、定義:資料分別
均方誤差、平方差、方差、均方差、協方差(轉)
相差 均方差 nbsp 無法 bsp 技術 方法 簡便 但是 一,均方誤差 作為機器學習中常常用於損失函數的方法,均方誤差頻繁的出現在機器學習的各種算法中,但是由於是舶來品,又和其他的幾個概念特別像,所以常常在跟他人描述的時候說成其他方法的名字。 均方誤差的數學表達為:
描述統計學:極差、方差、標準差
變異程度的度量(離散程度的度量) 交貨時間的變異性造成按時完成生產任務的不確定性 極差 極差=最大值-最小值 最簡單的變異程度的度量 但很少單獨用來度量變異程度。僅有兩個觀測值,異受極端值的影響 四分位數間距 能夠克服極端值的影響,因為四分位數是中間的50%資料的極差. 方差 是用所有資
期望、方差、協方差、標準差
期望, 方差, 協方差,標準差 期望 概率論中描述一個隨機事件中的隨機變數的平均值的大小可以用數學期望這個概念,數學期望的定義是實驗中可能的結果的概率乘以其結果的總和。 定義 設P(x) 是一個離散概率分佈,自變數的取值範圍為{x1,x2,...,xn }。其期望被定義為:
統計學習方法——均值、方差、標準差及協方差、協方差矩陣
一、統計學基本概念:均值、方差、標準差 統計學裡最基本的概念就是樣本的均值、方差、標準差。首先,我們給定一個含有n個樣本的集合,下面給出這些概念的公式描述: 均值: 標準差: 方差: 均值描述的是樣本集合的中間點,它告訴我們的資訊是有限的。 標準差給我們描述的是樣
平均值(Mean)、方差(Variance)、標準差(Standard Deviation)
本文目錄 開篇明志 對於一維資料的分析,最常見的就是計算平均值(Mean)、方差(Variance)和標準差(Standard Deviation)。在做【特徵工程】的時候,會出現缺失值,那麼經常會用到使用 平均值 或者 中位數等進行填充。
方差、標準差、均方差、均方誤差區別總結
參考了http://blog.csdn.net/Leyvi_Hsing/article/details/54022612 一、百度百科上方差是這樣定義的:(variance)是在概率論和統計方差衡量隨機變數或一組資料時離散程度的度量。概率論中方差用來度量隨機變數和其數學
方差、標準差和均方根誤差的區別總結
一、方差 方差(variance):是在概率論和統計方差衡量隨機變數或一組資料時離散程度的度量。概率論中方差用來度量隨機變數和其數學期望(即均值)之間的偏離程度。統計中的方差(樣本方差)是
方差、標準差、均方根誤差、平均絕對誤差的總結
單純介紹概念不易理解,所以應從實際應用出發介紹其區別。四者的不同可從研究物件和研究目的進行區分。 一 區別比較 方差 定義:方差在統計描述和概率分佈中各有不同的定義,並有不同的公式。 (1)統計學 統計學中的方差(樣本方差)是各個資料分別與其平均數之差的平方
oracle資料庫之統計分析(方差、標準差、協方差)
SELECT deptno, ename, --st_name || ' ' || last_name employee_name, hiredate, sal, STDDEV (sal) OVER (PARTIT
概率論中均值、方差、標準差介紹及C++/OpenCV/Eigen的三種實現
概率論是用於表示不確定性宣告(statement)的數學框架。它不僅提供了量化不確定性的方法,也提供了用於匯出新的不確定性宣告的公理。在人工智慧領域,概率論主要有兩種用途。首先,概率法則告訴我們AI系統如何推理,據此我們設計一些演算法來計算或者估算由概率論匯出的表示式。其次,
期望、方差、標準差、偏差、協方差和協方差矩陣
期望 一件事情有n種結果,每一種結果值為xixi,發生的概率記為pipi,那麼該事件發生的期望為: E=∑i=1nxipiE=∑i=1nxipi 方差 S2=1n∑i=1n(Xi−μ)2S2=1n∑i=1n(Xi−μ)2 其中:μμ為全體平均數
簡析方差、標準差與數值離散程度
方差(variance): 變數與其均值的差的平方和除以(變數數+1)。 如有一組資料: [1,2,3,4,5], 其均值就是 (1+2+3+4+5) / 5 = 3 所以其方差為: ((1-3)^2 + (2-3)^2 +(3-3)^2 + (4-3)^2 + (5-3)^2) /( 5+1
重溫概率學(一)期望、均值、標準差、方差
概率 隨機變數:實驗的結果稱為隨機變數。隨機變數分為: 離散隨機變數:如骰子。 連續隨機變數:如時間範圍。實數範圍(包含有理數和無理數) 因為隨機變數可以取不同的值,所以產出了概率分佈的概念,統計學家用概率分佈描述不同隨機變數發生的概率。因此有: 離散型概率分佈 連續型概率分佈 期望和均值
影象演算法的基礎知識(雙線性插值,協方差矩陣,矩陣的特徵值、特徵向量)
0. 前言 MATLAB或者OpenCV裡有很多封裝好的函式,我們可以使用一行程式碼直接呼叫並得到處理結果。然而當問到具體是怎麼實現的時候,卻總是一臉懵逼,答不上來。前兩天參加一個演算法工程師的筆試題,其中就考到了這幾點,感到非常汗顏!趕緊補習! 1. 雙線性插值 在影象處
ArcGIS 中的標準分類方法(相等、分位、自然斷裂、標準差)
ArcGIS:不規則向量多邊形裁切柵格資料方法比較 https://jingyan.baidu.com/article/e73e26c0d90b0524adb6a73a.html ArcGIS 中的標準分類方法(相等、分位、自然斷裂、標準差
統計量分析--極差、標準差、變異係數、四分位數間距
#-*- coding: utf-8 -*- #餐飲銷量資料統計量分析 import pandas as pd catering_sale = 'catering_sale.xls' #餐飲資料 da