一、設計任務

1、把任務十中的文字字元轉為國標碼，計算共需要多少位元。

2、用你所學的方法（霍夫曼編碼、遊長編碼或算數編碼）壓縮這些字元，得到的壓縮碼流共計多少位元。說明資料的冗餘度在哪裡。

3、手動編碼也可以。最好程式設計實現壓縮。

二、文字轉國標碼原理

1、漢字機內碼、區位碼、國標碼簡介

漢字的機內碼是漢字在計算機漢字系統內部的表示方法，是計算機漢字系統的基礎程式碼。

我國制定了“中華人民共和國國家標準資訊交換漢字編碼”，標準代號為GB2312—80，
這種編碼又稱為國標碼。在國標碼的字符集中共收錄了一級漢字3755個，二級漢字3008
個，圖形符號682個，三項字元總計7445個。
    在國標GD2312—80中規定，所有的國標漢字及符號分配在一個94行、94列的方陣中，方陣的每一行稱為一個“區”，編號為01區到94區；每一列稱為一個“位”，編號為01位到94位，方陣中的每一個漢字和符號所在的區號和位號組合在一起形成的四個阿拉伯數字就是它們的“區位碼”。區位碼的前兩位是它的區號，後兩位是它的位號。用區位碼就可以唯一地確定一個漢字或符號，反過來說，任何一個漢字或符號也都對應著一個唯一的區位碼。如上所述，漢字區位碼的區碼和位碼的取值均在1~94之間，如直接用區位碼作為機內碼 ，就會與基本ASCII碼混淆。為了避免機內碼與基本ASCII碼的衝突，需要避開基本ASCII碼中的控制碼(00H~1FH)，還需與基本ASCII碼中的字元相區別。為了實現這兩點，可以先在區碼和位碼分別加上20H，在此基礎上再加80H(此處“H”表示前兩位數字為十六進位制數)。由於漢字的區碼與位碼的取值範圍的十六進位制數均為01H~5EH(即十進位制的01~94)， 所以漢字的高位位元組與低位位元組的取值範圍則為A1H~FEH(即十進位制的161~254)。

2、漢字機內碼、區位碼、國標碼轉換規則

區碼 = 機內碼高位位元組 - 80H

位碼 = 機內碼低位位元組 - 80H

國標碼高位元組 = 區碼 + 20H
國標碼低位元組 = 位碼 + 20H

3、漢字轉換為國標碼中的特殊處理

由於文字檔案中含有數字、英文字母、空格等其它ASSIC碼值小於等於160的英文字元，所以在將文字中中文字元轉換為國標碼時遇到的英文字元不應作處理，應直接儲存起來，但這樣會與其它中文字元轉換後的國標碼相混淆（因為漢字的國標碼也小於160）。為此，在將文字內容轉換為國標碼的過程中，每遇到ASSIC碼值小於等於160的英文字元時，則在該英文字元前插入一個ASSIC碼值為0的空字元，作為原始檔案中非漢字字元的標記，即此字元的ASSIC值非漢字轉換後的國標碼。

三、Huffman編碼與解碼原理

1、Huffman編碼原理

       霍夫曼（D.A.Huffman）於1952年提出一種編碼方法，它完全依據字元出現概率來構造平均長度最短的異字碼頭，有時稱之為最佳編碼，一般叫做霍夫曼編碼。

霍夫曼編碼的基本思想是出現概率大的信源符號編寫較短的碼字，出現概率小的信源符號編寫較長的碼字，從而構造出平均長度最短的異字碼頭。

文字檔案可以看做是由一串位元組組成的位元組流，因此可以把位元組作為最基本的信源符號。文字檔案也可以看做是由一串中文字元組成，因此也可以把中文字元作為最基本的信源符號。但以位元組作為信源符號，比以中文字元作為信源符號具有如下優勢：

1、  以位元組作為信源符號編碼，基本符號只有256種；以中文字元作為信源符號，基本符號高達上萬種。因此以位元組作為信源符號構造的Huffman樹的節點數為256*2-1= 511個，遠遠小於以中文字元構造的Huffman樹的節點個數，可以大大減少構造Huffman樹和遍歷Huffman樹所需的時間。

2、  把中文字元對映為位元組符號，不僅減少了信源符號個數，還使原本不想關的中文字

符之間建立了相關性，增大了資料之間的冗餘性，因此可最大化的壓縮資料。

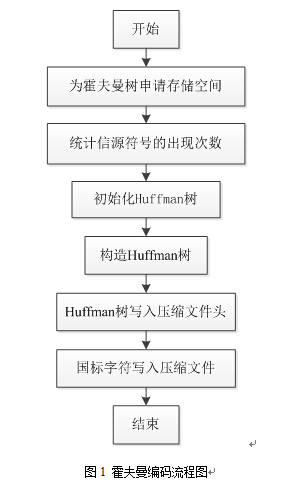
基於C++的霍夫曼編碼的基本實現步驟如下：

1、  為霍夫曼樹HT和單個信源符號的編碼HC申請儲存空間，HT= 512，HC = 256。

2、  統計信源符號的出現次數。

3、  初始化霍夫曼樹HT的每個節點，前256個節點的權重為對應信源符號的出現次數，

其餘節點權重為0。

4、按照信源符號出現概率構造Huffman樹。

5、遍歷Huffman樹，遍歷結果作為對應信源符號碼字，儲存在HC中。

5、將Huffman樹寫入壓縮檔案開始，作為Huffman解碼的標頭檔案。

6、讀取轉換後的國標檔案，將相應字元的編碼按位依次寫入壓縮檔案。

霍夫曼編碼軟體流程圖如圖1。

2、Huffman解碼原理

Huffman解碼是將Huffman編碼檔案還原為原始文字檔案，但在解碼時必須知道原始信源符號的Huffman編碼，因此在編碼過程中，需要將信源符號的編碼值或是Huffman樹一起寫到壓縮檔案中，如果將信源符號的編碼值寫入壓縮檔案，在解碼時需要挨個掃描對比解碼值，這樣勢必浪費解碼時間。如果將Huffman樹寫入壓縮檔案，解碼時只需還原Huffman樹，到時遍歷Huffman樹即可，相對於前一種來說具有較大優勢。因此，在這裡將Huffman樹寫入檔案的開始，作為檔案的編碼頭。這樣壓縮檔案主要由兩部分組成，第一部分是Huffman編碼頭，儲存Huffman樹，在解碼時用來還原Huffman樹；第二部分是壓縮資料，解碼時還原原始資料。

Huffman編碼頭是壓縮檔案中的額外開銷，因此應儘可能的小，Huffman樹的節點只有511個，所以Huffman樹的左節點、右節點、父節點可以選擇short long型儲存，而Huffman樹的權重只能用int型存數，這樣整個編碼頭需要（2+2+2+4）*511= 5100個位元組。考慮到遍歷Huffman樹時不需要知道Huffman樹的父節點和權重值，只需要知道左節點、右節點的值，這樣的話Huffman編碼頭中可以只儲存左節點和右節點，這樣整個編碼頭需要(2+2)*511 = 1022個位元組。

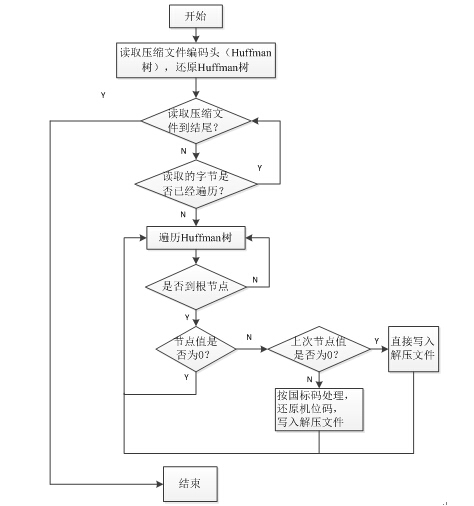
在解碼時，首先從壓縮檔案讀取編碼頭，還原Huffman樹，然後從壓縮檔案逐位元組讀取編碼，並逐位的掃描，遍歷Huffman樹，當節點值小於256時，說明已經掃描結束，準備輸出該節點序號值。如果該節點序號值等於0，說明後面的一個解碼值是英文字元，則該節點值不輸出，且下一個解碼值不做處理直接輸出。如果解碼出的節點序號值不等於0，說明該解碼值和後面解碼值是國標碼，應把國標碼還原為機內碼輸出。

基於C++的Huffman解碼具體步驟如下：

1、  讀取壓縮檔案編碼頭（Huffman樹），還原Huffman樹。

2、  按位元組讀取壓縮檔案，遍歷Huffman樹，直到遍歷到葉子節點。

3、  判斷葉子節點值是否為0。

4、  葉子節點值為0說明後面的一個解碼值是英文字元，則該節點值不輸出；繼續掃描到下一個解碼值，且不做處理直接寫入解壓檔案。

5、  葉子節點值不為0說明該解碼值和下一個解碼值是中文字元的國標碼，則將這兩個

解碼值還原為機內碼，寫入解壓檔案。

霍夫曼解碼軟體流程圖如圖2。

圖2霍夫曼解碼流程圖

四、實驗結果

經實際測試，本軟體可以很好地完成課題的要求，軟體除了可以壓縮和解壓課題中較少的文字外，也可以壓縮和解壓其他含有大量文字的文字檔案，具有較好的適用性。但由於是基於對Huffman樹遍歷的演算法，在壓縮和解壓檔案時會消耗掉大量的時間，當文字較大時，甚至壓縮和解壓時間讓人難以容忍。因此，如何使用新演算法提高壓縮和解壓時間是本設計需要額外考慮的，而不是隻侷限於本課題的要求。

軟體測試介面如圖3。

圖3 軟體測試介面

由軟體測試介面的列表框知道：

1、任務十中的文字轉換為國標碼後共有位元組數為：214

2、Huffman壓縮後得到的壓縮碼流共有位元組數為：156

3、Huffman對此文字文件的壓縮比為：1.371795

4、Huffman對此文字文件的編碼效率為：0.995011

原始檔內容如圖4。

圖4 原始檔內容

解壓檔案內容如圖5。

圖5 解壓檔案內容

由圖4和圖5對比知道，此軟體可以很好地將壓縮檔案還原為原始檔案。

實驗結果分析

由於此文字文件的信源符號是非等概率分佈的，所以信源符號的平均編碼長度大於資訊熵，即存在壓縮的可能性。由此可見，該文字信源符號的冗餘度隱含在信源符號的非等概率分佈之中，所以可以應用Huffman編碼無失真壓縮此檔案。

將中文字元對映為英文字元，減小了字元出現的區間範圍，將本沒有關係的中文字元中的一個位元組對映為相同的ASSIC碼值，這種對映關係使中文字元之間建立了聯絡，增大了資料之間的相關性，即資料間的冗餘度變大了，因此可以大大提高壓縮效率。且經試驗驗證，信源符號的平均編碼長度接近資訊熵。

C++原始檔下載地址：http://download.csdn.net/detail/u010213393/6431963