簡述LDA

LDA涉及的知識很多，對於作者這樣的菜鳥來說想要弄清楚LDA要費一番功夫，想簡單說清更是不易，寫下此文，也是希望在行文的過程中，把握LDA主要脈絡，理順思路。也希望我理解的方式與順序，能幫到一部分初學的朋友。如果有不對的地方，也歡迎作出指正。

什麼是LDA主題模型

首先我們簡單瞭解一下什麼是LDA以及LDA可以用來做什麼。

LDA(Latent Dirichlet Allocation)是一種文件生成模型。它認為一篇文章是有多個主題的，而每個主題又對應著不同的詞。一篇文章的構造過程，首先是以一定的概率選擇某個主題，然後再在這個主題下以一定的概率選出某一個詞，這樣就生成了這篇文章的第一個詞。不斷重複這個過程，就生成了整片文章。當然這裡假定詞與詞之間是沒順序的。

LDA的使用是上述文件生成的逆過程，它將根據一篇得到的文章，去尋找出這篇文章的主題，以及這些主題對應的詞。

現在來看怎麼用LDA，LDA會給我們返回什麼結果。

LDA是非監督的機器學習模型，並且使用了詞袋模型。一篇文章將會用詞袋模型構造成詞向量。LDA需要我們手動確定要劃分的主題的個數，超引數將會在後面講述，一般超引數對結果無很大影響。

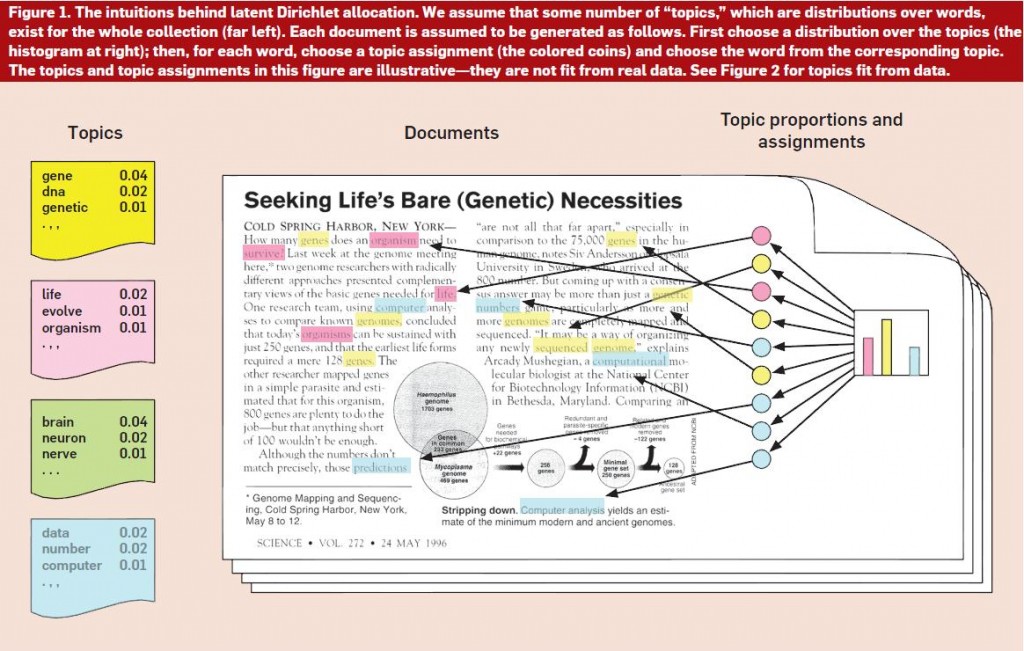
這裡寫圖片描述

上圖是推斷《Seeking Life’s Bare(Genetic)Necessities》（Figure 1）的例子。使用主題建模演算法（假設有100個主題）推斷《科學》上17000篇文章的潛在主題結構，然後推斷出最能描述圖1中示例文章的主題分佈（圖左）。需要注意的是，儘管主題分佈上有無窮個主題，但事實上只有其中的一小部分的概率不為零。進一步地，文章中詞可被分主題進行組織，可以看到最常見的主題所包含的概率最大的詞。

主題分佈與詞分佈

上面說了，一篇文章的生成過程，每次生成一個詞的時候，首先會以一定的概率選擇一個主題。不同主題的概率是不一樣的，在這裡，假設這些文章-主題符合多項式分佈。同理，主題-詞也假定為多項式分佈。所謂分佈（概率），就是不同情況發生的可能性，它們符合一定的規律。

如果你數學基礎和我一樣薄弱，可能你已經忘了什麼事多項式分佈，這裡我們首先回顧一下兩點分佈和二項分佈，多項式分佈是二項分佈的延伸。二項分佈是兩點分佈的延伸。

兩點分佈

已知隨機變數X的分佈率為

X	1	0
p	p	1-p

則有
E(x)=1∗p+0∗q=p
D(x)

=E(x2)−[E(x)]2=pq

拋一次硬幣的時候，不是正面就是反面，符合兩點分佈。這裡概率P為引數。

二項分佈

二項分佈，即是重複n次兩點分佈。設隨機變數X服從引數為n,p的二項分佈。其中，n為重複的次數，p為兩點分佈中，事件A發生的概率。設X=k為n次實驗中事件A發生了k次的概率。
可以得到X的分佈率為：
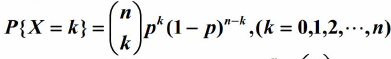
這裡寫圖片描述
例如，丟5次硬幣，事件A為硬幣正面朝上，則PX=k表示求拋5次硬幣，有k次硬幣正面朝上的概率。通過計算可以得知二項分佈的期望和方差如下，這裡就不計算了：
E(x)=np
D(x)=np(1−p)

多項式分佈

多項式分佈（multinomial）是二項分佈在兩點分佈上的延伸。在兩點分佈中，一次實驗只有兩種可能性，p以及（1-p）。例如拋一枚硬幣，不是正面就是反面。在多項式分佈中，這種可能的情況得到了擴充套件。例如拋一個骰子，一共有6種可能，而不是2種。

設某隨機實驗如果有k個可能情況 A1、A2、…、Ak，分別將他們的出現次數記為隨機變數X1、X2、…、Xk，它們的概率分佈分別是p1，p2，…，pk，那麼在n次取樣的總結果中，A1出現n1次、A2出現n2次、…、Ak出現nk次的這種事件的出現概率P有下面公式：
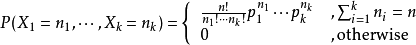
這裡寫圖片描述
這裡，p1,p2…pk都是引數

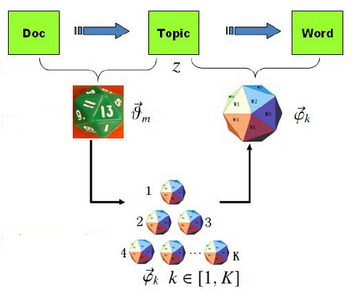
那麼現在我們回到LDA身上，前面已經說了主題和詞是符合多項分佈的，我們可以用骰子形象地表達一篇文章的生成的過程。

這裡寫圖片描述

有兩類骰子，一種是文章-主題（doc-topic）骰子，骰子的每面代表一種主題。這裡設一共有K個主題，則K面。骰子的各個面的概率記為ϑ⃗ =(p1,p2,p3,...,pk)。各個面的概率即為這個多項式分佈的引數。

另一種骰子為主題-詞(topic-word)骰子，一共有K個，從1~K編號，分別對應著不同的主題。骰子的一個面代表一個單詞。由於有K個骰子，把不同主題-詞骰子各個面的概率分別記為φ⃗ 1,φ⃗ 2,...φ⃗ k。對於一個主題-詞骰子，他的各個面的概率即為這個多項式分佈的引數。

那麼一篇文章的生成過程可以表示為：

拋擲這個doc-topic骰子，得到主題編號z
選擇編號為z的topic-word骰子，得到詞w
不斷重複步驟1以及步驟2

引數估計

上面我們已經知道了主題分佈和詞分佈都屬於多項式分佈，只是它們的引數究竟是什麼值，我們還無從知曉。如果我們能估算出它們的引數，我們就能求得這些主題分佈和詞分佈。LDA的主要目的就是求出主題分佈和詞分佈，距離這個目的，我們近在咫尺。

極大似然估計

我們知道，頻率可以用來估計引數。例如對於兩點分佈，拋硬幣。當我們拋的次數足夠多，可以估出p接近1/2，大數定理是有力的保證。頻率學派為引數估計提供了另一種有力的工具——極大似然估計。它的思想可以這樣形象地表達：既然樣本已經出來了，我們有理由相信它們發生的概率很大，於是我們不如就設給定引數的情況下，出現這些樣本的概率是最大的，通過求導計算極值，從而計算出引數。

這裡寫圖片描述

我們設詞和詞，文章和文章之間是獨立的。進一步，有了一個單詞的概率，我們就可以求一篇文章的概率：
p(w⃗ |dm)=∏j=1n∑k=1Kp(wj|zk)p(zk|dm)

進一步，有了整個語料庫（訓練集，多篇文章）的概率：
L=∏m=1M∏j=1n∑k=1Kp(wj|zk)p(zk|dm)

上面說過，極大似然估計就是要讓這個式子達到最大值。接下來還需要把式兩邊取對手，求導，解似然方程，就可以得到引數。實際上，到這裡為止，講述的是其實還只是plsa模型，因此這裡不寫出求解過程。LDA在plsa的求參上作了一些變化，下面將會講到。

形式化地，似然函式可以如下表示：
P(x1,x2,...xn|ϑ)
哪個引數能夠使得這個P最大，則把這個引數作為我們選定的引數。

貝葉斯估計

上一小節中我們知道，plsa模型用頻率學派來估計主題分佈和詞分佈的引數，頻率學派認為引數是一個定值。而貝葉斯學派則認為引數是變化的，也應該符合一定的分佈。LDA在plsa的基礎上引入了貝葉斯學派的方式。
我們先來看看貝葉斯公式

P(ϑ|x)=P(x,ϑ)P

LDA主題模型小結

簡述LDA

什麼是LDA主題模型

主題分佈與詞分佈

兩點分佈