機器學習實戰筆記7(Adaboost)
1:簡單概念描述
Adaboost是一種弱學習演算法到強學習演算法,這裡的弱和強學習演算法,指的當然都是分類器,首先我們需要簡單介紹幾個概念。
1:弱學習器:在二分情況下弱分類器的錯誤率會低於50%。其實任意的分類器都可以做為弱分類器,比如之前介紹的KNN、決策樹、Naïve Bayes、logiostic迴歸和SVM都可以。這裡我們採用的弱分類器是單層決策樹,它是一個單節點的決策樹。它是adaboost中最流行的弱分類器,當然並非唯一可用的弱分類器。即從特徵中選擇一個特徵來進行分類,該特徵能使錯誤率達到最低,注意這裡的錯誤率是加權錯誤率,為錯分樣本(1)與該樣本的權重的乘積之和(不明白看後面程式碼)。
更為嚴格點的定義:
強學習:一個概念如果存在一個多項式的學習演算法能夠學習它,並且正確率很高,那麼,這個概念是強可學習的; 弱學習:一個概念如果存在一個多項式的學習演算法能夠學習它,並且學習的正確率僅比隨機猜測略好(高於50%),那麼,這個概念是弱可學習的; 強可學習與弱可學習是等價的。並且理論證明可以將若干個弱學習分類器通過線性疊加提升為強學習分類器。2:強學習器:識別準確率很高並能在多項式時間內完成的學習演算法
3:整合方法:就是將不同的分類器組合在一起,這種組合的結果就是整合方法或者稱為元演算法。它可以是不同演算法的整合,也可以是同一演算法在不同設定下的整合,還可以是資料集的不同部分分配給不同分類器後的整合。
4:通常的整合方法有bagging方法和boosting方法,adaboost是boosting的代表演算法,他們的區別在於:bagging方法(bootstrapaggregating),中文為自舉匯聚法,是從原始資料集重選擇(有放回,可以重複)得到S個新資料集的一種技術,每個新資料集樣本數目與原資料集樣本數目相等,這樣就可以得到S個分類器,再對這S個分類器進行疊加,他們的權重都相等(當然這裡S個分類器採用的分類演算法不一樣的話,可以考慮使用投票),這樣就可以得到一個強學習器。
而boosting方法是通過集中關注被已有分類器錯分的那些資料來獲得新的分類器,boosting演算法中分類的權重並不相等,每個權重代表的是其對應分類器在上一輪迭代中的成功度。這裡不是太明白的話,看完後面adaboost演算法就會明白這句話的含義。
5:adaboost演算法:機器學習實戰這本書上的描述和論文中的描述是一致的,見下面(前兩幅是書中描述,後一副是論文中描述)。
問題:上題中的alpha為什麼是這個公式呢?解釋為:-----再看沒看懂!!
2:python程式碼的實現
(1) 基於單層決策樹構建分類器
def loadSimDat():
dataMat = matrix([[1, 2.1],
[2.0, 1.1],
[1.3, 1.0],
[1.0, 1.0],
[2.0, 1.0]])
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
return dataMat, classLabels
# 單層決策樹生成函式
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray
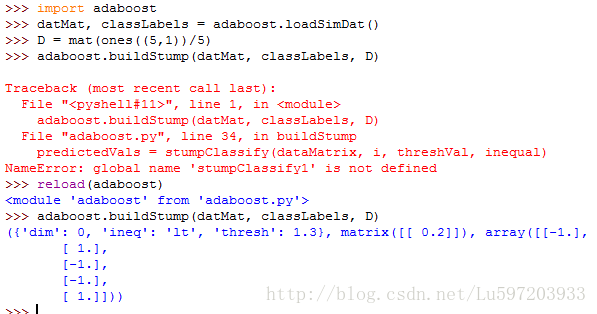
def buildStump(dataArr, classLabels, D):
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {}; bestClassEst = mat(zeros((m,1)))
minError = inf
for i in range(n):
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax - rangeMin)/numSteps
for j in range(-1, int(numSteps)+1):
for inequal in ['lt','gt']:
threshVal = (rangeMin + float(j)*stepSize)
predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal)
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T * errArr #這裡的error是錯誤向量errArr和權重向量D的相應元素相乘得到的即加權錯誤率
#print "split: dim %d, thresh %.2f, thresh inequal: %s, the weighted error is %.3f" %(i, threshVal, inequal, weightedError)
if weightedError < minError:
minError = weightedError
bestClassEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump, minError, bestClassEst注意這裡有三層迴圈構建了單層決策樹,最外層迴圈為遍歷特徵,次外層迴圈為遍歷的步長,最內層為是否大於或小於閥值。構建的最小錯誤率為加權錯誤率,這就是為什麼增加分錯樣本的權重,因為分錯樣本的權重增加了,下次如果繼續分錯,加權錯誤率會很大,這就不滿足演算法最小化加權錯誤率了。此外,加權錯誤率在每次迭代過程中一定是逐次降低的。。
(2) 完整adaboost演算法
# 基於單層決策樹的adaboost訓練過程
def adaBoostTrainDS(dataArr, classLabels, numIt = 40):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m,1))/m)
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
bestStump, error, classEst = buildStump(dataArr, classLabels, D)
# print "D:", D.T
alpha = float(0.5 * log((1.0 - error)/max(error, 1e-16))) #確保在沒有錯誤時不會發生除零溢位
bestStump['alpha'] = alpha
weakClassArr.append(bestStump)
#print "classEst:", classEst.T
expon = multiply(-1 * alpha * mat(classLabels).T, classEst) #乘法用於區分是否正確或者錯誤樣本
D = multiply(D, exp(expon))
D = D/D.sum() # 歸一化用的
aggClassEst += alpha * classEst #累加變成強分類器
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T, ones((m,1)))
errorRate = aggErrors.sum()/m
print "total error: ", errorRate, "\n"
if errorRate == 0.0: break
return weakClassArr, aggClassEst注意程式碼中的一個技巧max(error,le-16)用於確保在沒有錯誤時不會發生除零溢位。
(3) 測試演算法:基於adaboost的分類
#adaboost分類函式
def adaClassify(datToClass, classifierArr):
dataMatrix = mat(datToClass)
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix, classifierArr[i]['dim'], classifierArr[i]['thresh'], classifierArr[i]['ineq'])
aggClassEst += classifierArr[i]['alpha']*classEst
print aggClassEst
return sign(aggClassEst)3:案例—從疝氣病症預測病馬的死亡率
# 案例-通過馬疝病預測馬的死亡率
def loadDataSet(fileName): #general function to parse tab -delimited floats
numFeat = len(open(fileName).readline().split('\t')) #自動檢測特徵的數目
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat-1):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
注意上圖中會發現在錯誤率達到了一個最小值之後又開始上升,這種現象稱之為過擬合現象。
此外如何理論上證明弱學習分類器可以通過線性疊加提升為強學習分類器,有兩種證明方法:(1)通過誤差上界,(2)通過adaboost的損失函式來證明。推導看以參看:http://blog.csdn.net/v_july_v/article/details/40718799, 其中我只看了誤差上界的推導。
誤差上界的結論表明,AdaBoost的訓練誤差是以指數速率下降的。另外,AdaBoost演算法不需要事先知道下界γ,AdaBoost具有自適應性,它能適應弱分類器各自的訓練誤差率 。
只要保證弱分類器的錯誤率小於0.5,每次e^(2Mr^2))肯定是不斷減小的
註明:1:本筆記來源於書籍<機器學習實戰>
2:參考blog:http://blog.csdn.net/haidao2009/article/details/7514787
歡迎轉載或分享,但請務必宣告文章出處。 (新浪微博:小村長zack, 歡迎交流!)