牛頓迭代法求根——C語言
阿新 • • 發佈:2018-12-31
牛頓迭代法求根的原理:
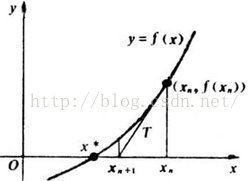 設r是
設r是
這個題目用到迭代法,說實話我的腦子轉的慢,我到現在還沒有學好這個方法。#include<stdio.h> #include<math.h> int main() { double solut(double,double,double,double );//函式原型宣告 double a,b,c,d; scanf("%lf%lf%lf%lf",&a,&b,&c,&d); printf("%.2f",solut(a,b,c,d)); return 0; } double solut(double a,double b,double c,double d) { double x=1,x0; do { x0=x; x=x0-(((a*x+b)*x+c)*x+d)/((3*a*x+2*b)*x+c); } while(fabs(x-x0)>=1e-5);//為點xn+1與xn之間的距離,當兩點的距離無限接近於0時,就時我們所要求的根x*。如果取x*這個點為例,我們發現方程在該點的切線與x軸的交點為x*,此時x與x0之間的距離為零。 return x; }
迭代法的類似題目: 1:迭代法求兩個數的最大公約數(輾轉相除法) 原理:設兩數為a、b(a>b),用a除以b,得a÷b=q......r1(0≤r1)。若r1=0,則(a,b)=b;若r1≠0,則再用b除以r1,得b÷r1=q......r2 (0≤r2).若r2=0,則(a,b)=r1,若r2≠0,則繼
 續用r1除r2,……如此下去,直到能整除為止。當然a與b的大小並不需要在意,因為在第一次輾轉相除後,二者的位置關係就發生了改變。
續用r1除r2,……如此下去,直到能整除為止。當然a與b的大小並不需要在意,因為在第一次輾轉相除後,二者的位置關係就發生了改變。
#include <stdio.h> #include <stdlib.h> int main() { int a,b; scanf("%d %d",&a,&b); int maxgys(int a,int b);//函式原型宣告 printf("%d",maxgys(a,b)); return 0; } int maxgys(int a,int b) { while(b!=0) { int r; r=a%b; a=b; b=r; } return a; }
2:Fibonacci數列也可以用到迭代法 原理:斐波那契數列(Fibonacci sequence),又稱黃金分割數列、因數學家列昂納多·斐波那契(Leonardoda Fibonacci)以兔子繁殖為例子而引入,故又稱為“兔子數列”,指的是這樣一個數列:1、1、2、3、5、8、13、21、34、……在數學上,斐波納契數列以如下被以遞迴的方法定義:F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)在現代物理、準晶體結構、化學等領域,斐波納契數列都有直接的應用。
#include <stdio.h>
#include <stdlib.h>
int main()
{
long n;
scanf("%ld",&n);
void fibonacci(long);
fibonacci(n);
return 0;
}
void fibonacci(long n)
{
long f1,f2,fn,i;
f1=1;
f2=2;
printf("%ld %ld ",f1,f2);
for(i=1;i<=n-2;i++)
{
fn=f1+f2;
f1=f2;
f2=fn;
printf("%ld",f2);
printf(" ");
}
}
