機器學習模型評價指標及R實現
1.ROC曲線
考慮一個二分問題,即將例項分成正類(positive)或負類(negative)。對一個二分問題來說,會出現四種情況。如果一個例項是正類並且也被 預測成正類,即為真正類(True positive),如果例項是負類被預測成正類,稱之為假正類(False positive)。相應地,如果例項是負類被預測成負類,稱之為真負類(True negative),正類被預測成負類則為假負類(false negative)。
列聯表如下表所示,1代表正類,0代表負類。
| 預測 | ||||
|---|---|---|---|---|
| 1 | 0 | 合計 | ||
| 實際 | 1 | True Positive(TP,真正類) | False Negative(FN,假負類) | Actual Positive(TP+FN) |
| 0 | False Positive(FP,假正類) | True Negative(TN,真負類) | Actual Negative(FP+TN) | |
| 合計 | Predicted Positive(TP+FP) | Predicted Negative(FN+TN) | TP+FP+FN+TN |
- 真正類率(true positive rate ,TPR), 也稱為 Sensitivity,計算公式為TPR=TP/ (TP+ FN),刻畫的是分類器所識別出的 正例項佔所有正例項的比例。
- 假正類率(false positive rate, FPR),計算公式為FPR= FP / (FP + TN),計算的是分類器錯認為正類的負例項佔所有負例項的比例。
- 真負類率(True Negative Rate,TNR),也稱為specificity,計算公式為TNR=TN/ (FP+ TN) = 1 - FPR。
在一個二分類模型中,對於所得到的連續結果,假設已確定一個閾值,比如說 0.6,大於這個值的例項劃歸為正類,小於這個值則劃到負類中。如果減小閾值,減到0.5,固然能識別出更多的正類,也就是提高了識別出的正例佔所有正例的比例,即TPR,但同時也將更多的負例項當作了正例項,即提高了FPR。為了形象化這一變化,在此引入ROC。
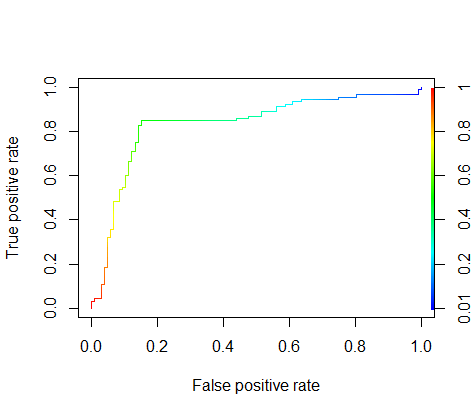
ROC曲線正是由兩個變數1-specificity(x軸) 和 Sensitivity(y軸)繪製的,其中1-specificity為FPR,Sensitivity為TPR。隨著閾值的改變,就能得到每個閾值所對應的1-specificity和Sensitivity,最後繪製成影象。
該影象的面積如果越接近1,那麼我們則認為該分類器效果越好。從直覺上來說,假設我們的預測全部100%正確,那麼不管閾值怎麼變(除了閾值等於0和1時),我們的Sensitivity(真正類)率永遠等於1,1-specificity(1-真負類率)永遠等於0,所以該圖就是個正方形,面積為1,效果最好。
樣例資料集:
library(ROCR)
data(ROCR.simple)
ROCR.simple<-as.data.frame(ROCR.simple)
head(ROCR.simple)
# predictions labels
# 1 0.6125478 1
# 2 0.3642710 1
# 3 0.4321361 0
# 4 0.1402911 0
# 5 0.3848959 0
# 6 0.2444155 1繪製ROC圖:
pred <- prediction(ROCR.simple$predictions, ROCR.simple$labels)
perf <- performance(pred,"tpr","fpr")
plot(perf,colorize=TRUE)2.AUC值
AUC值就是ROC曲線下的面積,可以通過以下程式碼計算:
pred <- prediction(ROCR.simple$predictions, ROCR.simple$labels)
auc.tmp <- performance(pred,"auc")
auc <- as.numeric([email protected])3.Recall-Precision(PR)曲線
同樣是一個二分類的模型的列聯表,我們可以定義:
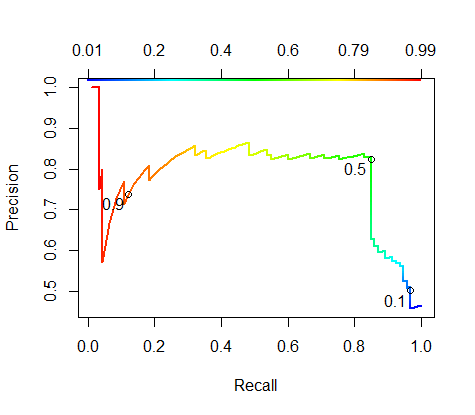
然後我們通過計算不同的閾值,以Recall為X軸,Precision為Y軸繪製圖像。
PR圖可以有這樣的應用,引用一個例子[1]:
1. 地震的預測
對於地震的預測,我們希望的是RECALL非常高,也就是說每次地震我們都希望預測出來。這個時候我們可以犧牲PRECISION。情願發出1000次警報,把10次地震都預測正確了;也不要預測100次對了8次漏了兩次。
2. 嫌疑人定罪
基於不錯怪一個好人的原則,對於嫌疑人的定罪我們希望是非常準確的。及時有時候放過了一些罪犯(recall低),但也是值得的。
對於分類器來說,本質上是給一個概率,此時,我們再選擇一個CUTOFF點(閥值),高於這個點的判正,低於的判負。那麼這個點的選擇就需要結合你的具體場景去選擇。反過來,場景會決定訓練模型時的標準,比如第一個場景中,我們就只看RECALL=99.9999%(地震全中)時的PRECISION,其他指標就變得沒有了意義。
繪製程式碼:
pred <- prediction(ROCR.simple$predictions, ROCR.simple$labels)
RP.perf <- performance(pred, "prec", "rec")
plot (RP.perf)
#檢視閾值為0.1,0.5,0.9下的召回率和精確率
plot(RP.perf, colorize=T, colorkey.pos="top",
print.cutoffs.at=c(0.1,0.5,0.9), text.cex=1,
text.adj=c(1.2, 1.2), lwd=2)一般這曲線越靠上,則認為模型越好。對於這個曲線的評價,我們可以使用F分數來描述它。就像ROC使用AUC來描述一樣。
4.F1分數
當
我們可以使用R計算F1分數:
pred <- prediction(ROCR.simple$predictions, ROCR.simple$labels)
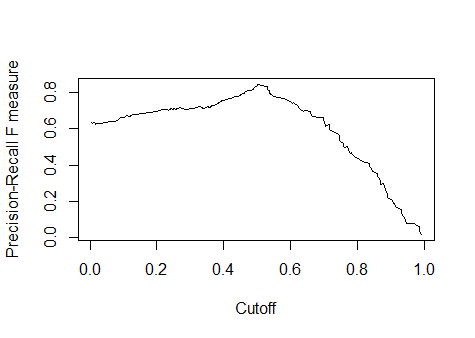
f.perf <- performance(pred, "f")
plot(f.perf) #橫座標為閾值的取值5.均方根誤差RMSE
迴歸模型中最常用的評價模型便是RMSE(root mean square error,平方根誤差),其又被稱為RMSD(root mean square deviation),其定義如下:
其中,
RMSE雖然廣為使用,但是其存在一些缺點,因為它是使用平均誤差,而平均值對異常點(outliers)較敏感,如果迴歸器對某個點的迴歸值很不理性,那麼它的誤差則較大,從而會對RMSE的值有較大影響,即平均值是非魯棒的。 所以有的時候我們會先剔除掉異常值,然後再計算RMSE。
R語言中RMSE計算程式碼如下:
pred <- prediction(ROCR.simple$predictions, ROCR.simple$labels)
rmse.tmp<-performance(pred, "rmse")
rmse<[email protected]6.SAR
SAR是一個結合了各類評價指標,想要使得評價更具有魯棒性的指標。(cf. Caruana R., ROCAI2004):
其中準確率(Accuracy)是指在分類中,使用測試集對模型進行分類,分類正確的記錄個數佔總記錄個數的比例:
pred <- prediction(ROCR.simple$predictions, ROCR.simple$labels)
sar.perf<-performance(pred, "sar")7.多分類的AUC[5]
將二類 AUC 方法直接擴充套件到多類分類評估中, 存在表述空間維數高、複雜性大的問題。 一般採用將多類分類轉成多個二類分類的思想, 用二類 AUC 方法來評估多類分類器的效能。Fawcett 根據這種思想提出了 F- AUC 方法[4], 該評估模型如下:
其中
參考資料
[1]精確率、召回率、F1 值、ROC、AUC 各自的優缺點是什麼?作者:金戈戈
[2]ROC曲線和PR(Precision-Recall)曲線的聯絡
[3]機器學習模型評價(Evaluating Machine Learning Models)-主要概念與陷阱
[4]Fawcett T. Using Rule Sets to Maximize ROC Performance[C]// IEEE International Conference on Data Mining. IEEE Computer Society, 2001:131.
[5]秦鋒, 羅慧, 程澤凱,等. 一種新的基於AUC的多類分類評估方法[J]. 計算機工程與應用, 2008, 44(5):194-196.
[6]百度百科ROC曲線
作為分享主義者(sharism),本人所有網際網路釋出的圖文均遵從CC版權,轉載請保留作者資訊並註明作者a358463121專欄:http://blog.csdn.net/a358463121,如果涉及原始碼請註明GitHub地址:https://github.com/358463121/。商業使用請聯絡作者。