前幾節我們分析了向量空間模型（VSM）、基於奇異值分解（SVD）的潛語意分析（LSA）、基於概率的潛語意分析（PLSA）這些模型都是為了解決文字分類問題，他們各自有自己的優點和缺點，其中VSM模型簡單方便但是容易造成維度爆炸和計算量慢的缺點，LSA是基於矩陣分解的原理進行分析的，優點是對VSM有效的降維，但是計算量還是很大，因此引入了PLSA，該優點是完全避開了PSA的矩陣分解的計算問題，把其完全轉變為概率問題，通過EM演算法進行求解問題，但是該演算法的缺點是假設太過牽強，建模比較粗糙，統計理論基礎不足，沒有考慮在NLP中語料稀疏的情況，EM演算法迭代計算繁瑣，計算量大，因此還需要繼續尋找更好的模型，這時LDA（Latent Dirichlet Allocation）應運而生，這個演算法更精密優雅，但又不容易理解的模型LDA（Latent Dirichlet Allocation），LDA可以說是統計理論大觀園，需要有較好的概率統計基礎才可以理解，好下面我們就看看他是如何解決問題的，這裡我想了很久怎麼寫這篇文章，本人這裡為了能讓大家理解LDA的工作過程，本節主要使用語言描述型和少量公式進行講解，先讓大家從整體上去把握這個演算法，然後我們在一起去推倒公式，如果整體性不清晰，很容易暈的，本人剛開始學習的時候就在這裡暈了兩三天，因此我會考慮當時我理解的過程進行講解，這裡的講解，會使用到前面大量的使用過的術語，例如矩陣的奇異值分解後得到兩個矩陣的情況（下圖），第一個矩陣的行是item（主題、電影、單詞），列是隱分類或是topic或者抽象的特徵等等稱號，第二個矩陣的行是隱分類或是topic或者抽象的特徵等等稱號，列就是user（使用者、document等等），這裡大家對前面的知識點應該有一個清晰的認識，因為他們都是遞進關係，就是為了解決前一個演算法的缺點才會引入更好的演算法，這也是我一直在強調的學習演算法時儘量去搞懂演算法的來歷和發展歷史，這樣我們才能對這個系列的演算法有一個清晰的認識，以後遇到問題才能根據問題的特點，想到類似的解決方案，下面給出對應的矩陣分解的示意圖，不懂請看我前面的文章。好，廢話不多說，這裡開始我們今天的內容，這裡大家一定要耐著性子看，因為我感覺他的難度和支援向量機是同一個級別了。

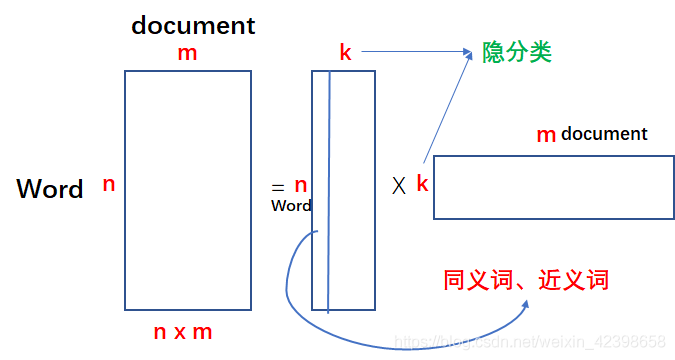
LDA（Latent Dirichlet Allocation）

LDA（Latent Dirichlet Allocation）是一種文件主題生成模型，也稱為一個三層貝葉斯概率模型，包含詞、主題和文件三層結構。所謂生成模型，就是說，我們認為一篇文章的每個詞都是通過“以一定概率選擇了某個主題，並從這個主題中以一定概率選擇某個詞語”這樣一個過程得到。文件到主題服從Dirichlet分佈，主題到詞服從Dirichlet分佈。LDA是一種非監督機器學習技術，可以用來識別大規模文件集（document collection）或語料庫（corpus）中潛藏的主題資訊。它採用了詞袋（bag of words）的方法，這種方法將每一篇文件視為一個詞頻向量，從而將文字資訊轉化為了易於建模的數字資訊。但是詞袋方法沒有考慮詞與詞之間的順序，這簡化了問題的複雜性，同時也為模型的改進提供了契機。每一篇文件代表了一些主題所構成的一個概率分佈，而每一個主題又代表了很多單詞所構成的一個概率分佈。

對於語料庫中的每篇文件，LDA定義瞭如下生成過程（generative process）：

1.對每一篇文件，從主題分佈中抽取一個主題；

2.從上述被抽到的主題所對應的單詞分佈中抽取一個單詞；

3.重複上述過程直至遍歷文件中的每一個單詞。

語料庫中的每一篇文件與T（通過反覆試驗等方法事先給定）個主題的一個多項分佈 （multinomial distribution）相對應，將該多項分佈記為θ。每個主題又與詞彙表（vocabulary）中的V個單詞的一個多項分佈相對應，將這個多項分佈記為φ.

上面是簡單的百度百科的解釋，下面我們將從頭開始介紹什麼是LDA：

Beta分佈和Dirichlet 分佈

這裡推薦大家看看《LDA數學八卦》這篇文章的0.3部分的背景知識，這裡我就不講背景了，直接給出結果，大家需要找到這篇文章結合學習：

Beta分佈

這裡簡單的講一下背景，詳細請參考文件，遊戲的規則很簡單，我有一個魔盒，上面有一個按鈕，你每按一下按鈕，就均勻的輸出一個[0,1]之間的隨機數，我現在按10下，我手上有10個數，你猜第7大的數是什麼，偏離不超過0.01就算對。”你應該怎麼猜呢？

使用概率進行對其描述為事件E：

得到事件E的概率：

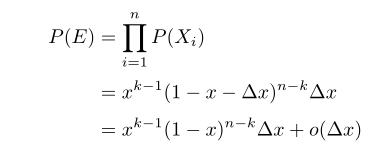
 現在我們進行對其進行擴充套件，就是說，如果有n個數落進了,那麼對應的概率密度函式為如下：

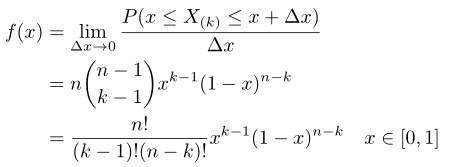
這就是對應的n個數落進了的概率密度，具體推倒請看文件，上面的形式我們覺得很複雜了，而且分子分母都是階乘的形式，因此這裡我們可以使用Gamma進行代替，這裡大家可以這樣簡單的理解一下Gamma函式，gamma函式是階乘的延續，如果輸入的是整數，則返回的該數的階乘，如果輸入的不是整數，返回的是複雜的和階乘相關的數。這裡不細講了，有興趣的同學建議看看那篇文章的前一部分，下面直接給出，大家可以直接接受即可（和我們接受均勻分佈、正態分佈一樣接受他即可）：

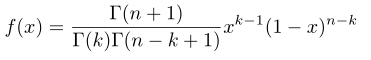
這裡感覺還是麻煩，因為引數的形式不一樣，這裡繼續簡化，這裡去，代入上式得：

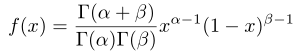
 這就是Beta分佈了，那麼這個分佈有什麼物理意義呢？這裡通過例子進行解釋一下：

這裡舉一個兩點分佈的例子即擲硬幣的，這裡的硬幣不是均勻的，正面可能的概率是0.4，反面為0.6，我不知道硬幣的這個引數即概率，我試圖通過試驗去找出這個引數，根據大數定律，當我擲1萬次時，如果出現4000次的正面，6000次的反面就說明我們的引數正面是0.4，反面是0.6，但是現在的問題，因為某些原因，你無法做那麼多的試驗，只能做10次試驗，即你只能擲10次硬幣，這個時候如果出現4次反面和6次正面，你敢說這個硬幣的概率正面是0.4，反面為0.6嗎？不敢的，因為試驗次數太少，這時怎麼辦呢？這時候，我們假設硬幣的兩點的概率P是服從Beta分佈即服從上式，這裡大家需要注意的是服從Beta分佈的是概率P，不是其他，就是我們要求的正反兩面的概率P，  上式的引數是給定的引數，這裡我們假如n=10，其中k=7，則，，那麼我通過試驗的正面是0.4的概率代入上式計算，硬幣正面是0.4的概率有多大：

這樣我就能計算試驗10次的結果出現4次正面的概率為0.4的概率有多大了，上式的結果就是說明硬幣的概率引數P取值0.4的概率是多少，這裡大家必須得理解。

好，到這裡大家有沒有疑問呢？就是我的 為什麼是取值是7和4呢，這裡呢就和Beta分佈的共軛性質有關即Beta-Binomial 共軛性。

這裡需要給大家再次強調一下什麼是Beta分佈，Beta分佈的變數是概率P，如上面的例子，即在試驗次數較少的情況下，得到的硬幣概率P（這裡指根據統計得到的值，如上面投擲10次，4次正面 ，說明正面的概率為0.4），那麼得到的這個P是真實的P的概率是服從Beta分佈的，也就是說Beta分佈的變數是概率P，即可以寫成Beta(P)或者這樣寫，這裡大家把這個和正態分佈的寫法對比一下即，這樣大家應該理解我一直在強調的什麼意思了，其中P是Beta分佈的變數，是先驗的試驗為了描述方便，我們合起來寫即：

這裡的p就是我們猜測的概率，或者說我們初次得到的概率，也叫做先驗概率，那麼我們現在的試驗是符合二項分佈的，那麼這裡就有一個性質了即：

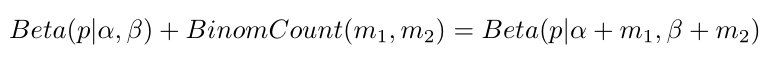
 其中就是試驗分別出現的次數，如硬幣正反面的次數，對應的就是正反面出現的次數，上面的式子就是Beta-Binomial共軛了，那麼這代表什麼呢？

假如現在有一個硬幣我們不知道他的分佈特性即正反兩面的概率，現在我先給定一個先驗概率，這個概率是服從Beta分佈的，那麼我使用這個硬幣進行實驗，分別記錄出現正反面的次數,那麼得到的新的分佈依然符合Beta分佈的，這樣有什麼好處呢？其實我們的給出的先驗是服從Beta分佈的，那麼再加上物理的試驗過程使其得到的分佈依然服從Beta分佈，只不過裡面的會根據物理試驗進行變化，但是始終符合Beta分佈，這樣話我們就容易分析了，因為分佈模型不變，分析手段就是一樣的，如果先驗分佈是其他的分佈，再加上物理試驗得到不確定的分佈我們怎麼分析呢？這就是使用Beta分佈的原因。這裡還是具體的舉個例子吧，假如我們擲硬幣，假如出現正反的次數都為1，先驗的概率為0.5，此時，，那麼我們

我們做試驗，記錄正反面的次數，這裡按照上面的例子加入，那麼我們帶進上式得到：

這樣就會得到分佈p=0.5的概率，這樣如果我們，簡單來說，就是如果我們的先驗概率不準確，但是我們可以根據我們的試驗去不斷的糾正，使概率可能性越小，這樣我們找到一個概率使的Beta分佈得概率最大，即,如下圖所示：

 這裡大家應該能明白吧，不明的我也沒辦法了，私聊我吧，這裡在說一下為什麼要選用Beta分佈的原因，其本質原因是，Beta分佈和兩點分佈是共軛的，即先驗概率和物理試驗過程結合後還是符合這個Beta分佈的，這裡大家需要理解，下面我們繼續，我們知道這裡的p是二值函式（即硬幣只有正反兩個值稱為二值）的，那如果是多值函式怎麼辦呢？這時就引入了Gamma分佈。

Dirichlet 分佈

Dirichlet 分佈的定義式是：

這就是多點了，之前的Beta分佈的p就兩個要麼是p要麼是1-p，而這裡的p就很多了，因此我們這裡寫成向量的形式，同樣的Beta分佈的就兩個，而這裡的是K個，因此也可直接寫成向量形式，因此 Dirichlet 分佈算是Beta分佈的擴充套件，理解是一樣的，這樣按照上面的理解就好，同樣的他也有一個和Beta分佈類似的性質即Dirichlet-Multinomial 共軛，如下：

這裡不詳細的解釋了，先驗概率滿足 Dirichlet 分佈，在和物理過程結合後任然滿足Dirichlet 分佈。

這兩個分佈大家應該都理解了，這裡建議大家看看那篇文章，你會理解的更深的，相信我，你會有驚喜的。下面我們來看看另外一個知識點即Gibbs Sampling

Gibbs Sampling（吉布斯取樣）

這個取樣我在深度學習相信的講解了，大家有興趣的可以看看我之前的寫的，這裡只是簡單講解一下這個取樣過程，當然這需要你具有一些基礎性的取樣知識，不懂的請看我的這篇文章，下面我就簡單的講講Gibbs Sampling，這裡保證大家能看懂的，好，廢話不多說，下面開始：

在實際生活中，大量問題包含隨機性因素。有些問題很難用數學模型來表示，也有些問題雖建立了數學模型，但其中的隨機性因素較難處理，很難得到解析解，這時使用計算機進行隨機模擬是一種比較有效的方法。隨機模擬方法是一種應用隨機數來進行模擬實驗的方法，也稱為蒙特卡羅法。這種方法名稱來源於世界著名的賭城——摩納哥的蒙特卡羅，通過對研究問題或系統進行隨機抽樣，然後對樣本值進行統計分析，進而得到所研究問題或系統的某些具體引數、統計量等。

也就是說我們的概率密度太複雜，導致我們寫出來或者無法計算，這裡我們就無法得到對應的統計特性，但是現在我們就是想知道他的統計特性，怎麼辦呢，如果我們能夠得到符合這個很複雜的概率密度的樣本，那麼我們根據樣本來統計這個概率密度的統計特性也是可以的，因此取樣就這樣由來了，上面的連結我簡單的講解了一些常用地取樣方法，但是那些方法都是針對一維的概率密度進行抽樣，但是如果高維就無法使用了，但是有針對高維進行抽樣的方法即Gibbs Sampling，這裡我只簡單的講講結果，儘量讓大家知道他的工作流程。

首先我們從二維的吉布斯取樣開始，然後推向高維的吉布斯取樣，首先這裡預設大家都懂了一維的吉布斯取樣了，二維和高維的取樣思想其實很簡單，就是我能不能把高維的取樣降到一維，通過一維來取樣就簡單了，因此高維的取樣就是這個思想，下面我們以二維的為例進行講解：

假如我有一個聯合分佈，我想求出符合這個聯合概率密度的統計特性，但是這個概率密度太複雜了，無法數學求出， 因此如果我能拿到服從這個聯合概率密度的樣本，那麼在通過樣本就可以估計這個聯合概率密度的統計特性了，但是現在的問題是他是二維的，如何處理呢？這樣做：

這裡我們知道符合聯合概率分佈的一個值假如是,帶進聯合概率密度，此時就變成一維的聯合概率密度了，如下：

根據上式我們知道了 ，其中聯合概率密度知道的帶進去可計算分子，分母也很容易知道，因此此時整個式子就變為一維的概率分佈了，然後就可以通過一維的取樣技術取樣了，此時就能得到,然後我把當做已知的量，當做未知量，按照下式：

同理此時取樣就可以得到,以此類推進行下去，因此它的圖形應該是兩個軸的變化來回更替，如下圖：

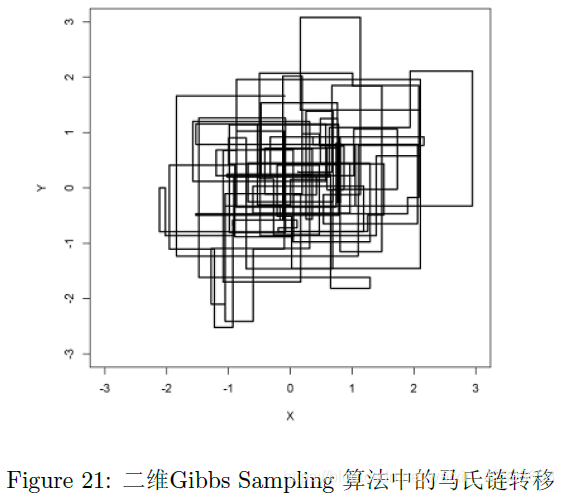
具體二維吉布斯取樣演算法如下：

同理推向高維即如下：

 這裡沒講取樣細節，其實高維取樣很麻煩的，這裡沒有展開講，建議大家看看我的深度學習方面的部落格，那裡我詳細的講解而了，這裡就不詳細講解了。下面我們就就簡單的講解一下我們的LDA模型，上面的內容都是鋪墊，下面的講解都是從總體性講解的，目的是希望大家能搞懂LDA的工作原理的，然後我們再去研究他的數學論證以及學習方法，這樣才是正確的學習方法，否則一旦沒有全域性把控，亂了，你會看不下去的，好，下面繼續，下面只從整體的工作原理開始，大家一定要把握住他的整體性。

LDA模型整體理解

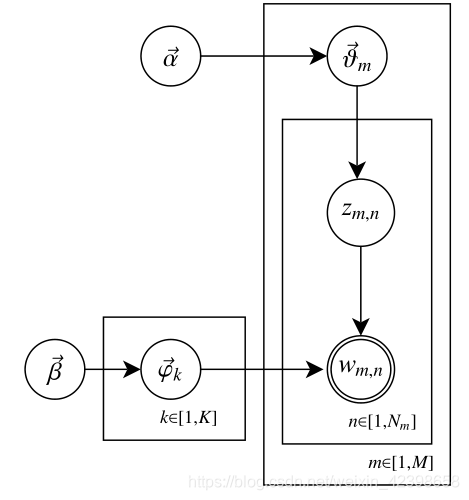
 其中，代表文件數目，代表主題數目，詞彙表中有個詞，表示第篇文件的單詞個數，和表示第篇文件中第個單詞及其主題。表示主題中所有單詞的概率分佈，表示第篇文件的所有主題概率分佈。和分別服從超引數和的Dirichlet先驗分佈。

這裡大家首先要做的就是先理解一下符合的意義，這裡先和大家強調一下就是上圖的和分別服從超引數和的Dirichlet先驗分佈，我們前面講的基礎就用到了，這裡大家應該理解使用Dirichlet分佈的意義在哪裡，這個分佈有什麼特性，最大的特性就是在先驗的概率基礎上加上物理過程，最後的分佈仍符合Dirichlet分佈。我們從開始講，這裡的代表第m篇文章的所有主題（隱分類）的概率，那麼從到是什麼意思呢？其中如本節剛開的矩陣分解圖的等號右邊第二個矩陣，即隱分類和文字，那麼從到是從第m篇文章中第n個詞，去生成對應這篇文章的第n個詞的主題的概率。這裡使用擲骰子為例進行說明，就是說我有M個骰子，每篇文章看成一個骰子，而每個骰子有K個面，這裡每個面代表一個詞，這裡的每個骰子都是服從Dirichlet分佈，且每個骰子搖出來的面的概率不同，現在開始物理試驗過程，我拿出屬於對應每篇文章的骰子進行搖號，我需要搖多少次呢，搖到和本篇文章的詞數相同，那麼我搖出的骰子代表什麼意思呢？代表在第m篇文章中的第n個詞屬於哪個主題這就是，就這樣把所有的文章按照這樣的方法進行做一遍。好到這裡我們停一下，再看看另外一個服從Dirichlet分佈代表什麼。

從上面介紹符號我們知道表示主題中所有單詞的概率分佈，也就是說會產生k個骰子，這k個骰子分別對應著K個主題（隱分類），那麼就是給這些主題找對應的單詞，也就是說我現在知道第m篇文章第n個位置輸入哪個主題，但是我不知道這個位置的單詞，這個單詞怎麼確定呢？就是通過進行確定這個單詞即，而這個詞從哪裡找呢？是從詞彙表表中找即V。詞典裡的詞和文章裡的詞不同，詞典的詞是不會重複，是根據語料的出來的。

這裡需要在強調一下，就是首先我們是給文章的詞去尋找對應的主題（隱分類）即和，那麼當我們需要給第m篇第n個詞尋找對應的主題時，此時我們把對應這一篇文字的另外一個服從Dirichlet分佈，從詞典中尋找對應這個位置的，符合這個主題的單詞即，同時也從中得到這個單詞，進行訓練，總體上LDA的思想就是這樣，下面我從整體思路再理一下，希望大家能理解他的工作原理：

首先我們只擁有很多篇文字和一個詞典，那麼我們就可以在此基礎上建立基於基於文字和詞向量聯合概率（也可以理解為基於文字和詞向量的矩陣，大家暫且這樣理解），我們只知道這麼多了，雖然知道了聯合概率密度了，但是還是無法計算，因為我們的隱分類或者主題不知道啊，在LSA中使用SVD進行尋找隱分類的，在PLSA中使用概率進行找隱分類的，而在LDA中是如何做的呢？他是這樣做的，首先我為每個文字賦值一個服從Dirichlet分佈的，他的作用就是尋找文字中對應詞的主題（隱分類），或者從本篇文字的角度來說確定這篇文字有哪幾個隱分類，而隱分類的確定是根據進行確定的，首先我們根據確定了這個這篇文章的某一個位置的詞了即，那麼我通過詞典，在通過去尋找這個詞對應的隱分類（主題），這樣我就確定了這篇文章的隱分類，同時都計算了所有的相關概率，後面就可以通過隱分類和相關概率進行判斷文字的相似性等等就和前面幾節一樣了，這就是LDA的深層工作原理，這樣說大家應該可以理解了吧，寫吐了，本節結束，下一節我們主要從數學方面對LDA的學習演算法和訓練演算法進行講解，當然也是很難理解的，我儘量深入淺出講解，大家如果有感覺，建議看論文輔助理解，這樣效果會更好。這篇論文是：

《Parameter estimation for text analysis》Gregor Heinrich Technical Report
Fraunhofer IGD
Darmstadt, Germany
[email protected]