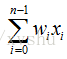分類問題是監督學習的一個核心問題。在監督學習中，當輸出變數取有限個離散值時，預測問題便成為分類問題。

監督學習從資料中學習一個分類決策函式或分類模型，稱為分類器（classifier）。分類器對新的輸入進行輸出的預測，這個過程稱為分類。

KNN演算法（k-NearestNeighbor）：

如果一個樣本在特徵空間中的k個最相鄰的樣本中的大多數屬於某一個類別，則該樣本也屬於這個類別。

所選擇的鄰居都是已經正確分類的物件。

對於類域的交叉或重疊較多的待分樣本集來說，KNN方法較其他方法更為適合。

        現在有電器，水果，書籍3個種類的點，分佈在第一象限（x表示價格，y表示銷量），現在已知一個點m，我們需要找出離它最近的點（歐氏距離），根據這幾個點的特徵去分析，如果k=4，找4個點，其中3個 點屬於水果類，那麼，我們就斷定這個點m也是水果。

KNN演算法不僅可以用於分類，還可用於迴歸。通過找出一個樣本的k個最近鄰居，將這些鄰居的屬性的平均值賦給該樣本，就可以得到該樣本的屬性。更有用的方法是將不同距離的鄰居對該樣本產生的影響給予不同的權值(weight)，如權值與距離成反比。

缺點：樣本分佈不均衡（有的類樣本很少，有的超多），就會影響最後判斷的結果。

樸素貝葉斯演算法：

公式：                                  P(B|A) = P(A|B)*P(B) / P(A)

即：                                      P(類別|特徵) = P(特徵|類別)*P(類別) / P(特徵)

           這個等式成立的條件需要特徵之間相互獨立,所以各屬性之間相關性較小時，樸素貝葉斯效能比較好

即要滿足這樣：                   P(A)=P(A1*A2*A3...) = P(A1)*P(A2)*P(A3)...

上面的公式可以改成：       P(B|A) = P(A1|B)*P(A2|B)*P(A3|B)...  / P(A1)*P(A2)*P(A3)...

優點：分類過程中時空開銷小（假設特徵相互獨立，只會涉及到二維儲存）

決策樹：

                        https://mp.csdn.net/postedit/85130080

人工神經網路：

目前，已有近40種神經網路模型，其中有反傳網路、感知器、自組織對映、Hopfield網路、波耳茲曼機、適應諧振理論等

數學定義：

來自其他處理單元（神經元）i的資訊為Xi，每一條突觸的權重（作用強度）是Wi，

                          左邊：   

                           右邊：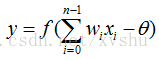                 

 θ（threshold）表示隱含層神經節點的閾值（大於這個值一種結果，小於這個值又一種結果，例如：買東西，價格小於10就買，大於10不買），f 稱為啟用函式

啟用函式：

      由於上一層的輸出是下一層的輸入，導致上層到下層是一個線性過程，而線性模型的表達能力不夠，所以引入非線性函式。

      常用的有：

              1）tanh（雙切正切函式）：tanh在特徵相差明顯時的效果會很好，在迴圈過程中會不斷擴大特徵效果

              2）sigmoid（s型函式）： 它可以將一個實數對映到(0,1)的區間，可以用來做二分類

              3）ReLU （簡單，大於0的留下，否則為0） 用於隱層神經元輸出

從輸入輸出的結果中進行學習：

                            神經元權值和閾值的不斷調整

學習規則：

 1） 誤差修正型規則：屬於有監督的學習方法，根據實際輸出和期望輸出的誤差進行網路連線權值的修正，

                                         δ學習規則、Widrow-Hoff學習規則、感知器學習規則和誤差反向傳播的BP(Back Propagation)學習規則

  2）競爭型規則：屬於無監督學習，沒有期望輸出，學習(訓練)階段與應用(工作)階段成為一體

  3）Hebb型規則：利用神經元之間的活化值(啟用值)來反映它們之間聯接性的變化，根據活化值(啟用值)來修正其權值

  4）隨機型規則：根據目標函式（即網路輸出均方差）的變化調整網路的引數，最終使網路目標函式達到收斂值

神經網路的運作：

最困難的部分就是確定權重（w）和閾值（θ）。目前為止，這兩個值都是自己主觀給出的，但現實中很難估計它們的值，一般採用試錯法，即微小的調整，得到效果最好的那一次調整。

支援向量機（Support Vector Machine, SVM）：

SVM是用來解決二分類問題的有監督學習演算法

支援向量機方法是建立在統計學習理論的VC 維理論和結構風險最小原理基礎上的，根據有限的樣本資訊在模型的複雜性（即對特定訓練樣本的學習精度，Accuracy）和學習能力（即無錯誤地識別任意樣本的能力）之間尋求最佳折衷，以期獲得最好的推廣能力（或稱泛化能力）。

泛化誤差界的公式為：

                                     R(w)≤Remp(w)+Ф(n/h)

公式中R(w)就是真實風險，Remp(w)就是經驗風險，Ф(n/h)就是置信風險。統計學習的目標從經驗風險最小化變為了尋求經驗風險與置信風險的和最小，即結構風險最小。

SVM正是這樣一種努力最小化結構風險的演算法。

非線性，是指SVM擅長應付樣本資料線性不可分的情況，主要通過鬆弛變數（也有人叫懲罰變數）和核函式技術來實現

維數高可以降維處理

線性分類器：

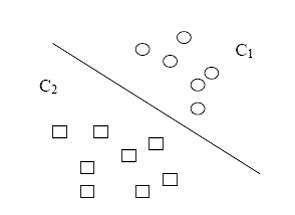
C1和C2是要區分的兩個類別，中間的直線就是一個分類函式，如果存在一個線性函式能夠將樣本完全正確的分開，就稱這些資料是線性可分的，否則稱為非線性可分的。

線性函式：一維是一個點，二維是線，三維是面,高於三維稱為超平面。一個線性函式是一個實值函式（即函式的值是連續的實數），通過分類函式執行時得到的值大於還是小於這個閾值來確定類別歸屬。

要將兩類分開，就要找到一個超平面，使得超平面到兩類的 margin 達到最大，margin就是超平面與離它最近一點的距離

演算法方面：https://blog.csdn.net/liugan528/article/details/79448379