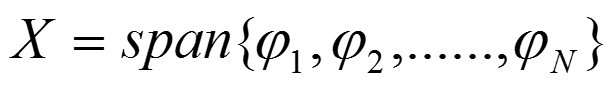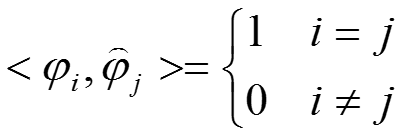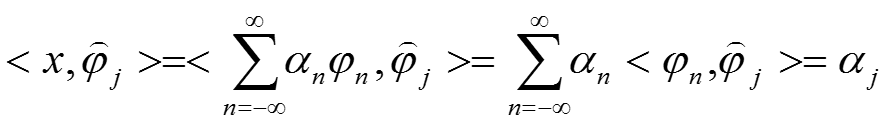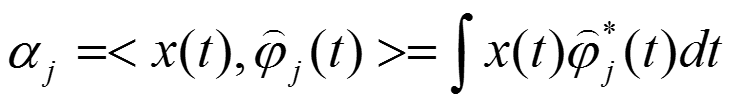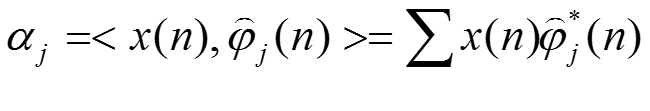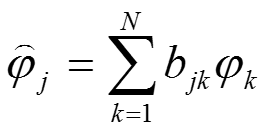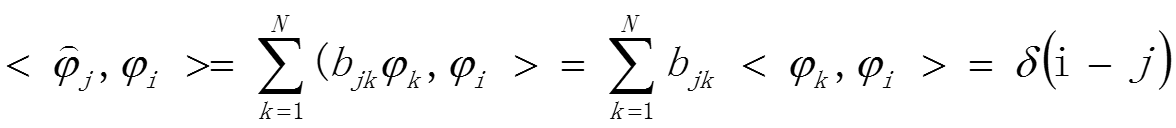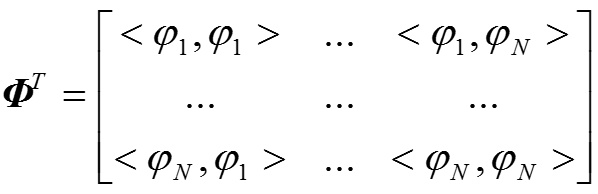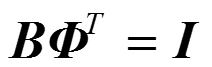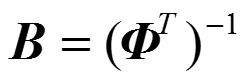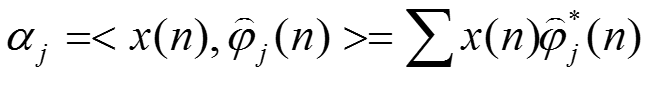1.訊號分解及完備性

設是X由一組向量所張成，即：

如果線性獨立，我們則稱它們為空間中的一組基”。
那麼訊號x可以離散表示如下：

若是一組兩兩互相正交的向量，展式稱為x的正交展開。分解係數是在各個基向量上的投影。
設向量和向量滿足如下雙正交關係：

那麼，我們對原始訊號就行投影變換（內積）：
看看，我們把最關心的分解係數給弄出來了！現在的問題是與原始基雙正交的向量怎麼求？

1.1 訊號分解、對偶基（倒數基）、正交基

關於訊號的分解表示，我們可以從連續時間和離散時間分開分析： 對於連續時間訊號：
對於離散時間訊號：
以上兩式稱為訊號的變換。“變換”的結果即是求出一組係數。 
稱為的“對偶基”

，或“倒數基”。
雙正交關係指的是兩組基之間各對應向量之間具有正交性，但每一組向量之間並不一定具有正交關係。
N 維空間中的正交基：
如果一組基向量的對偶向量即是其自身，也那麼這一組基向量構成了N 維空間中的正交基。

1.2 完備性/標架

若X空間中的任一元素x都可由一組向量作式 :
的分解，那麼我們稱這一組向量是“完備（complete）”的。 如果是完備的，且是線性相關的，那麼，由表示x必然會存在資訊的冗餘，並且其對偶向量將 不會是唯一的。這時，我們稱構成空間的一個“標架（frame）”。
若是完備的，且是線性無關的，則是X中的一組基向量，這時，存在且唯一，即存在
的雙正交關係。則對偶及存在，且是唯一

的。
對於正交關係，那麼他的對偶基就是自己本身。

1.3 詳細證明

將對偶基向量，用基向量表示：
將基向量與對偶基進行內積計算：
令：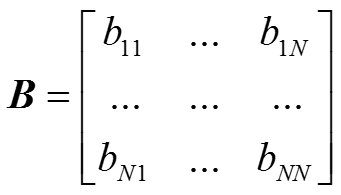     
這樣，我們可以得到如下公式：

這樣我們就可以通過基向量，求得他的對偶基向量。

2.思考

2.1為什麼訊號分解係數線性相關情況下，對偶基不唯一？

基向量現象相關，導致B矩陣是奇異矩陣，那麼得到的“對偶基向量”必定不唯一。

2.2為什麼訊號分解係數雙正交情況下，對偶基唯一？

單位陣I，那麼此時的B是固定的唯一的，就是基向量的逆。

2.3為什麼訊號分解係數正交情況下，對偶基就是本身？

正交情況下，矩陣的逆就是矩陣的轉置，那麼就是自己本身，如此簡單的運算，也正是正交變換在硬體領域很受歡迎的原因。因為對矩陣求轉置的複雜度要遠遠低於逆運算。

2.4分解係數可以通過對偶基向量和原始訊號的內積求得，這有什麼物理意義？

通過上面公式，我們可以通過物理角度進行思考。所謂的投影運算也可以看成是相似性衡量問題。如果對偶基向量與原始訊號越相似，分解係數應該越大！