資料結構與演算法20-圖的最短路徑
最短路徑
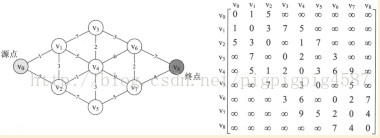
對於網圖來說,最短路徑,是指兩頂點之間經過的邊上權值之和最少的路徑,並且我們稱路徑上的第一個頂點是源點,最後一個頂點是終點。
迪傑斯特拉演算法
它並不是一下子就求出V0到V8的最短路徑,而一步步求出它們之間頂點的最短路徑,過程中都是基於已經求出的最短路徑的基礎上,求得更遠頂點的最短路徑,最終得到你要的結果。
我們來看一下思路
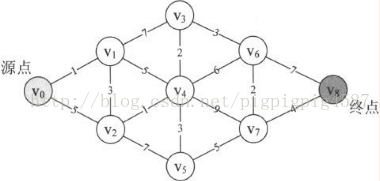
1. 頂點v0到v1的最短距離,答案是1,路徑就是直接v0連線到v1
2. 由於頂點v1還與v2、v3、v4連線,所以
我們同時求得了
v0->v1->v2=1+3=4,
v0->v1->v3=1+7=8
v0->v1->v4=1+5=6
現在,問v0到v2的最短距離是?答案是4
由於頂點v2還與v4、v5連線,所以此時我們同時求得v0->v2->v4 = 4+1=5
v0->v2->v5=4+7=11。這裡v0->v2我們用的是剛才計算出來 的較小的4。此時我們也發現v0->v1->v2->v4=5要比v0->v1->v4=6還要小。所以v0到v4目前的最小距離是5。如圖
當我們要求v0到v3的最短距離時,通向v3有三條邊,除v6沒研究過外,
v0->v1->v3=結果是8
v0->v4->v3=5+2=7。因此v0到v3的最短距離是7
我們來看一下程式碼模擬執行
#define MAXVEX 9 #define INFINITY 65535 typedef int Patharc[MAXVEX]; //用於儲存 最短路徑下標的陣列 typedef int ShortPathTable[MAXVEX]; //用於儲存到各點最短路徑的權值 /*Dijkstra演算法,求有向圖G的V0頂點到其餘頂點v最短路徑P[v]及帶權長度D[v]*/ /*P[v]的值為前驅頂點下標,D[v]表示v0到v的最短路徑長度和*/ void ShortesPath_Dijkstra(MGraph G,int v0,Patharc *P,ShortPathTable *D) { int v,w,k,min; int final[MAXVEX]; //final[w]=1表示頂點v0到vw的最短路徑 for(v=0;v<G.numVertexes;v++) { final[v]=0; //全部頂點初始化為未知最短路徑狀態 (*D)[v] = G.arc[v0][v]; (*P)[v] = 0; } (*D)[v0]=0; final[v0]=1; /**開始主迴圈,每次求得v0到某個v頂點的最短路徑/ for(v=1;v<G.numVertexes;v++) { min=INFIITY; for(w=0;w<G.numvertexes;w++) { if(!final[w]&&(*D)[w]<min) { k=w; min = (*D)[w]; } } final[k]=1; //將目前找到的最近的頂點置為1 for(w=0;w<G.numVertexes;w++) { if(!final[w]&&(min+G.arc[k][w]<(*D)[w])) { (*D)[w]=min*G.arc[k][w]; (*P)[w] = k; } } } }
分析過程:
1. 程式開始執行,第4行的final陣列是為了v0到某頂點是否已經求得最短路徑的標記,如果v0到vw已經有結果,則final[w]=1;
2. 第5~10行,是在對資料進行初始化的工作。此時final陣列值均為0,表示所有的點都未求得最短路徑。D陣列為{65535,1,5,65535,65535,65535,65535,65535}。因為v0與v1和v2的邊權值為1和5。P陣列全是0,表示目前沒有路徑。
3. 第11行,表示v0到v0自身,權值和結果為0。D陣列為{0,1,5,65535,65535,65535,65535,65535}。第12行,表示v0點算是已經求得最短路徑,因此final[0]=1。此時final陣列為{1,0,0,0,0,0,0,0,0}此時整個初始化操作完成
4. 第13行~33,為主迴圈,每次迴圈求得v0與一個頂點的最短路徑。因此v從1而不是0開始。
5. 先令min=65535的極大值,通過w迴圈,與D[w]比較找到最小值min=1,k=1。
6. 第24行,由k=1,表示與v0最近的頂點是v1,並且由D[1]=1,適量此時v0到v1的最短距離是1。因此將v1對應final[1]設定為1。此時final陣列為{1,1,0,0,0,0,0,0,0}
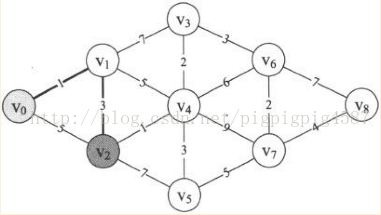
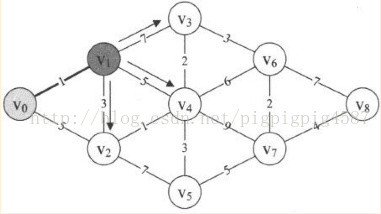
7. 第25~32行是一迴圈,此迴圈甚為關鍵。它的目的是在剛才已經找到的v0到v1的最短路徑的基礎上,對v1與其它頂點的邊進行計算,得到v0與它們的最短距離,如圖
因為此時min=1,所以本來的D[2]=5,現在v0->v1->v2=D[2]=min+3=4;
v0->v1->v3=D[3]=min+7=8, v0->v1->v4=D[4]=min+5=6,因此D陣列當前值為{0,1,4,8,6,65535, 65535, 65535, 65535}。而P[2]=1,P[3]=1,P[4]=1,它表示意思是v0到v2,v3,v4點的最短路徑它們的前驅是v1。此時P陣列值為{0,0,1,1,1,0,0,0,0}
8. 重新開始迴圈,此時v=2。第15~23行,對w迴圈,注意思為final[0]=1和final1[1]=1,由第18行的!final[w]可知,v0與v1並不參與最小值獲取。通過迴圈比較,找到最小值min=4,k=2。
9. 第24行,由k=2,表示已經求出v0到v2的最短路徑,並且由D[2]=4,知道最短距離是4。因此將v2對應的final[2]設定為1,此時final陣列為{1,1,1,0,0,0,0,0,0}
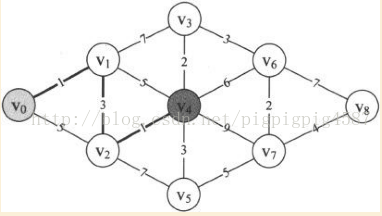
10. 第25~32行。在剛才已經找到V0與v2的最短路徑的基礎上,對v0與其他頂點的邊,進行計算,得到v0與它們的當前最短距離,如圖。因為min=4,所以本來D[4]=6,現在v0->v2->v4=D[4]=min+1 = 4; v0->v2->v5=D[4]=min+7 = 11,因此D陣列當前值為:{0,1,4,8,5,11, 65535, 65535, 65535}。而原來的P[4]=1而現在的P[4]=2,P[5]=2,它表示v0到v4、v5點的最短路徑它們的前驅均是v2。此時P陣列值為:{0,0,1,1,2,2,0,0,0}。
11. 重新開始迴圈,此時v=3。第15~23行,得到最小值min=5,k=4。
12. 第24行,由k=4已經求出v0到v4的最短路徑,並且由D[4]=5知道最短距離是5。因此將v4對應的final[4]設定為1。此時final陣列為{1,1,1,0,1,0,0,0,0}
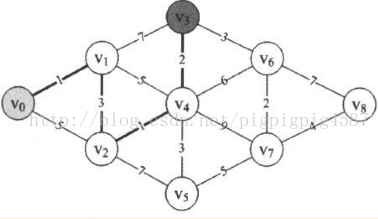
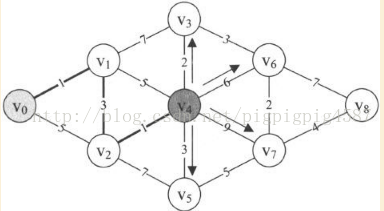
13. 第25~32行,對v4與其他頂點的邊進行計算。得到v0與它們的當前最短距離,因為min=5,所以本來D[3]=8,現在v0->v4->v3=D[3]=min+2=7,本來的D[5]=11,現在的v0->v4->v5=D[5]=min+3=8,另外v0->v4->v6=D[6]=min+6=11,v0->v4->v7=D[7]=min+9=14。因此D陣列的當前值為:{0,1,4,7,5,8,11,14,65535}。而原本的P[3]=1,此時P[3]=4,原本的P[5]=2,此時的P[5]=4,另外P[6]=4,P[7]=4,它表示v0到v3、v5、v6、v7點的最短路徑它們的前驅是v4。此時P陣列的值為:{0,0,1,4,2,4,4,4,0}
14. 之後的迴圈就是完全類似的了。得到最終結果
final陣列{1,1,1,1,1,1,1,1,1},它表示所有頂點均完成了最短路徑的查詢工作。此時D陣列為{0,1,4,7,5,8,10,12,16},它表示v0到各個頂點的最短路徑數,
此時的P陣列為{0,0,1,4,2,4,3,6,7}。比如P[8]=7它的意思是V0到V8的最短路徑,頂點v8的前驅頂點是v7,再由P[7]=6,表示v7的前驅是v6,P[6]=3,前驅是v3。這樣就可以得到,v0到v8的最短路徑為v8<-v7<-v6<-v3<-v2<-v1<-v0即v0->v1->v2->v4->v3->v6->v7->v8。
其實最終返回的陣列D和P,是可以得到V0到任意一個頂點的最短路徑和路徑長度的。例如v0到v8的最短路徑並沒有經過v5,但我們已經知道v0到v5的最短路徑。D[5]=8,由P[5]可知道它的前驅頂點是v4。所以v0到v5的最短路徑是v0->v1->v2->v4->v5。
迪傑斯特拉(Dijkstra)演算法解決了從某個源點到其餘頂點的最短路徑問題。時間複雜度O(n2)
現在如果我想求任決一點到其它點的最短路徑。則還得有一個迴圈來處理複雜度就變成了O(n3)
那麼我們再求一種求最短路徑的演算法如下
弗洛伊德(Floyd),它求所有頂點到所有頂點的時間複雜度也是O(n3),但其演算法非常簡潔優雅。
弗洛伊德(Floyd)演算法
我們先來看一個簡單的安全如下圖的3個頂點的連通網圖。
我們先定義兩個二維陣列D[3][3]和P[3][3],D代表頂點到頂點的最短路徑權值
P代表對應頂點的最小路徑前驅矩陣。
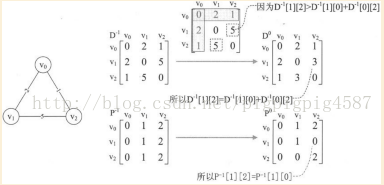
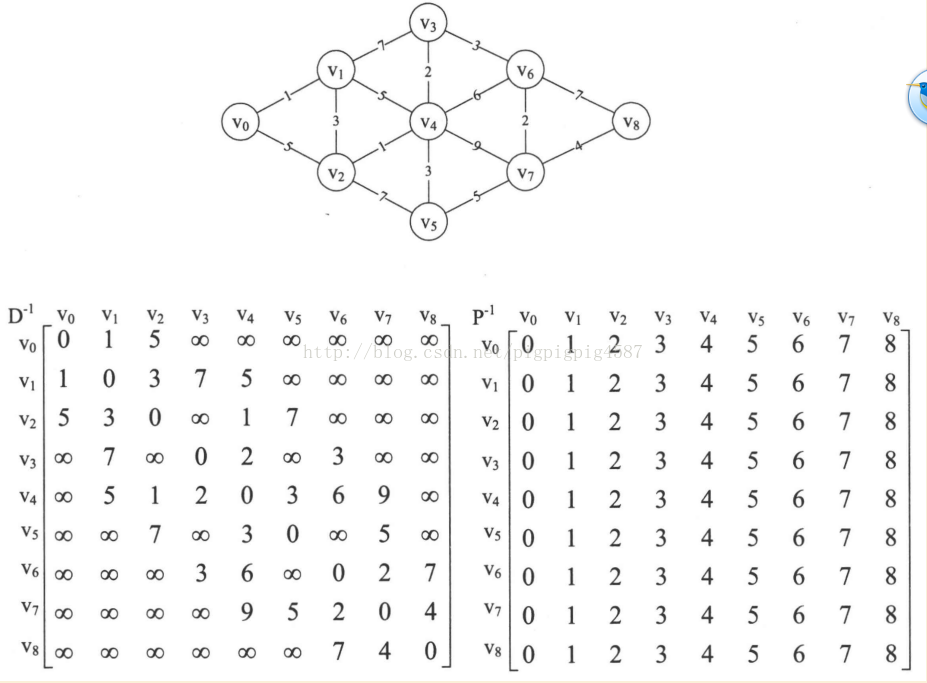
在未分析任何頂點前,我們將D命名為D-1其實它就是初始的圖的鄰接矩陣。將P命名為P-1,初始化為圖中所示的矩陣
首先我們來分析,所有頂點經過v0後到達另一頂點的最短路徑。因為只有三個頂點,因此需要檢視v1->v0->v2,得到D-1[1][0]+D-1[0][2]=2+1=3。
D-1[1][2]表示的是v1->v2的權值為5,我們發現D-1[1][0]>D-1[1][0]+D-1[0][2]。通俗的說就是v1->v0->v2比直接v1->v2的距離還要近。所以我們就讓D-1[1][2]=D-1[1][0]+D-1[0][2]=3,同樣的D-1[2][1]也等於3。於是就有了D0的矩陣
因為有了變化,所以P矩陣對應的P-1[1][2]和P-1[2][1]也修改為當前中轉的頂點v0的下標0,於是就有了P0看上圖的轉換過程
接下來有了D0和P0的基礎上繼續處理所有頂點經過v1和v2後到另一頂點的最短路徑,得到D1和P1、D2和P2完成所有頂點 到所有頂點的最短路徑計算工作
下面來個複雜的圖的推演
程式碼如下
typedef int Pathmatirx[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
/*Floyd演算法,求網圖G中各頂點v到其餘頂點w最短路徑P[v][w]及帶權長度D[v][w]*/
void ShortestPath_Floyd(MGraph G,Pathmatirx *P,ShortPathTable *D)
{
int v,w,k;
for(w=0;v<G.numVertexes;++v)
{
for(w=0;w<G.numVertexes;++w)
{
(*D)[v][w] = G.matirx[v][w]; //初始化,即為對應點間的權值
(*P)[v][w] = w; //初始化P
}
}
for(k=0;k<G.numVertexes;++k)
{
for(v=0;v<G.numVertexes;++v)
{
for(w=0;w<G.numVertexes;++w)
{
if((*D)[v][w]>(*D)[v][k]+(*D)[k][w])
{
(*D)[v][w] = (*D)[v][k]+(*D)[k][w];
(*P)[v][w]=(*P)[v][k];
}
}
}
}
}
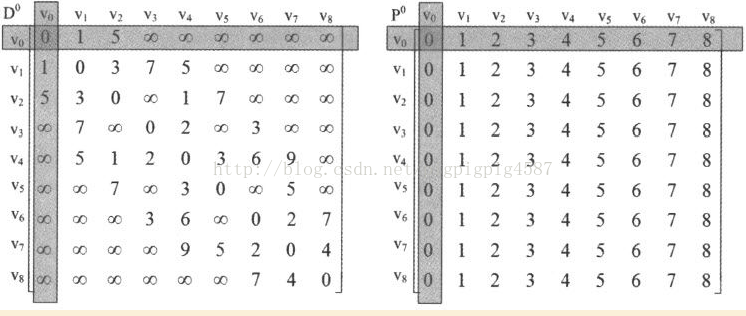
1. 程式開始執行,第4~11行就是初始化D和P,使得它們成為下圖的兩個矩陣。從矩陣也得到v0->v1路權值是1,v0->v2路權值是5,v0->v3無邊連線,所以路徑權值為極大值65535。
2. 第12~25行,是演算法的主迴圈,一共三個巢狀,k代表的就是中轉頂點的下標。v代表起始頂點,w代表結束頂點。
3. 當K=0時,也就是所有的頂點都經過v0中轉,計算是否有最短路徑的變化。可惜結果是,沒有任何變化,如下圖
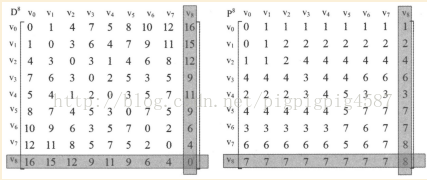
4. 當K=1時,也就是所有的頂點都經過v1中轉。此時,當v=0,原本D[0][2]=5,現在由於D[0][1]+D[1][2]=4。因此由程式碼的第20行,二者取其最小值,得到D[0][2]=4,同理可得D[0][3]=8、D[0][4]=6,當v=2、3、4時,也修改一些資料。對權值進行修改也要對P[v][k]
至此,我們的最短路徑就算是完成了,你可以看到矩陣第v0行的數值與迪傑斯特拉演算法求得的D陣列是完全相同的{0,1,4,7,5,8,10,12,16}
路徑v0到v8 P[0][8]=1 先經過v1,然後將1取代0得到P[1][8]=2說明經過2,然後以2取代1 P[2][8]=4說明經過4,然後以4取代2 P[4][8]=3說明經過3…
最後昨到v0->v1->v2->v4->v3->v6->v7->v8