資料結構與演算法一一圖
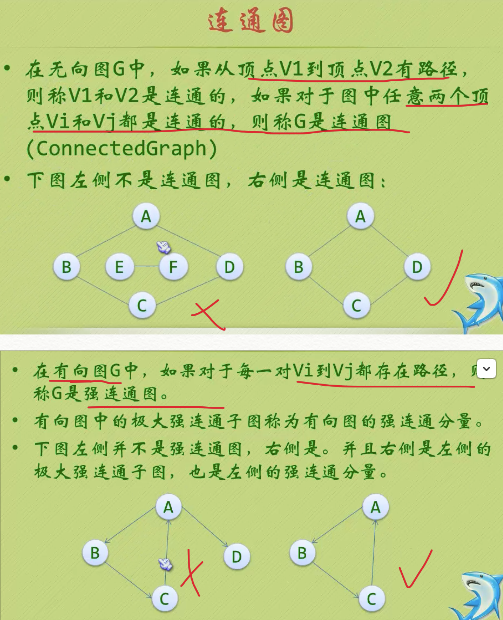
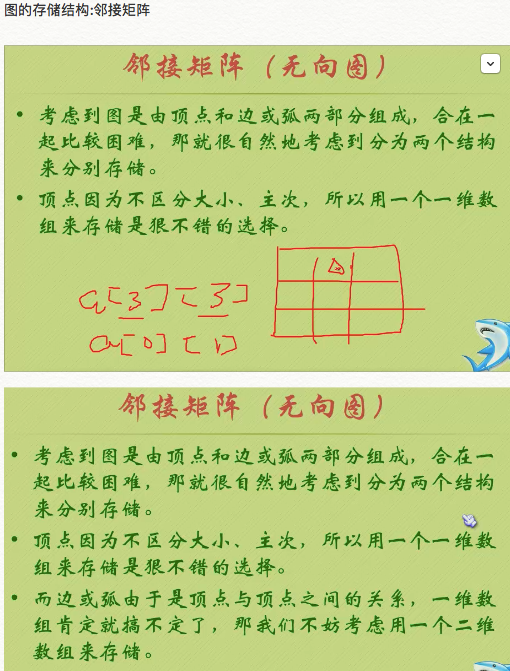
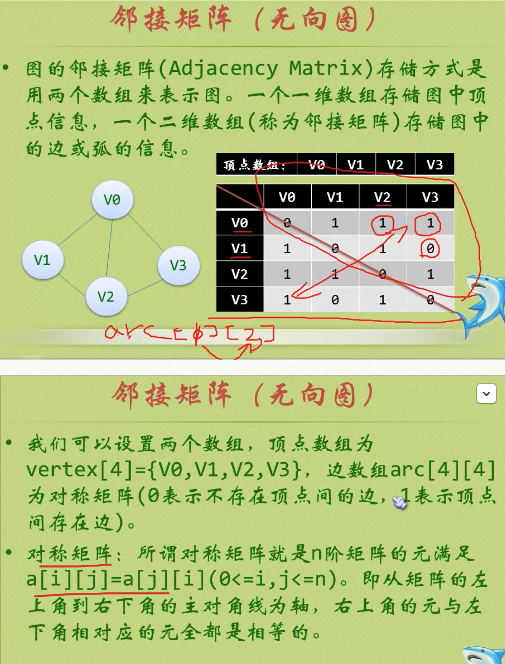
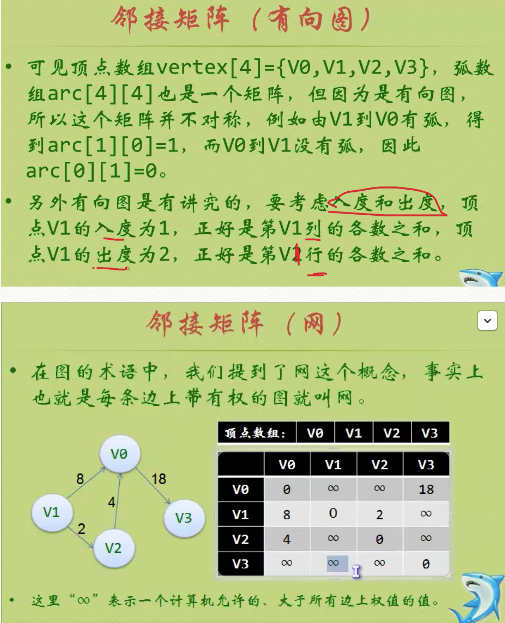
二、圖的儲存結構<鄰接矩陣>
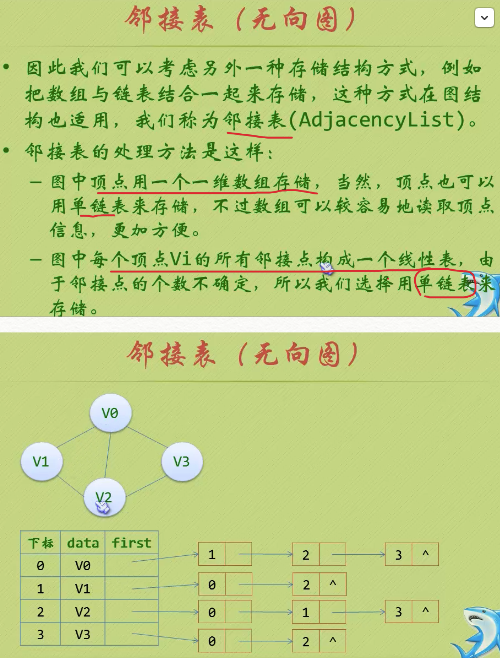
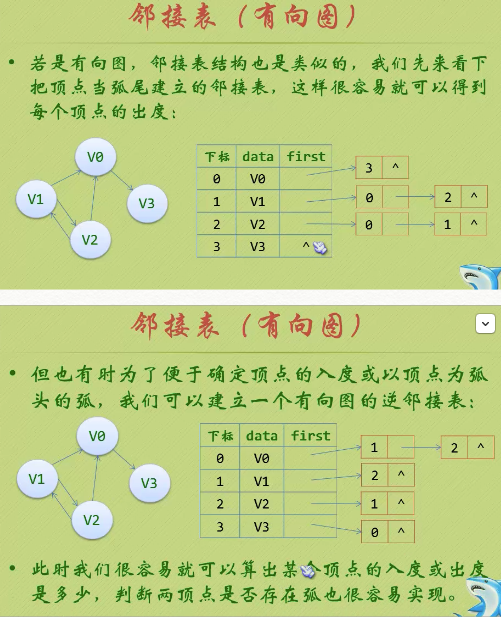
三、圖的儲存結構<鄰接表>
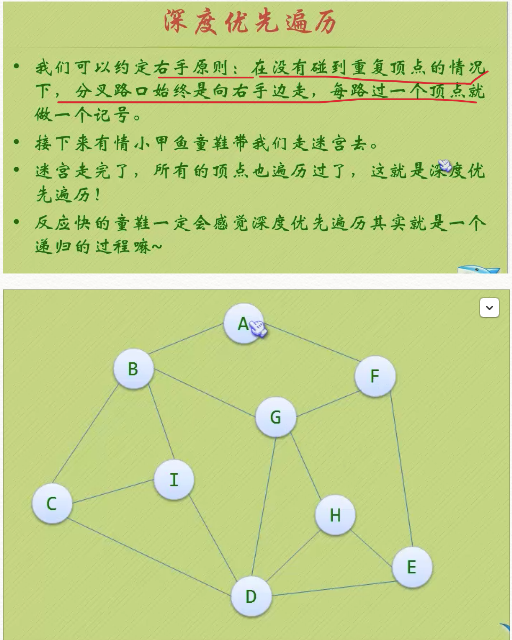
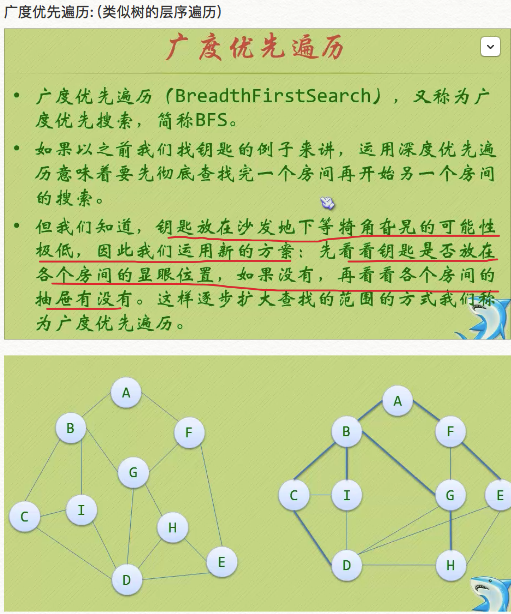
四、圖的遍歷
// ---------------------鄰接矩陣儲存結構------------------------ typedef char VertexType; // 頂點型別 typedef int EdgeType; // 邊上的權值型別 #define MAXVEX 100 // 最大頂點數 #define INFINITY 65535 // 用 65535 代表無窮 typedef struct { VertexType vexs[MAXVEX]; // 用來存頂點的陣列 EdgeType arc[MAXVEX][MAXVEX]; // 鄰接矩陣, 可看作邊表 int numVertexes, numEdges; // 圖中當前的頂點數和邊數 } MGraph; // 鄰接矩陣的廣度遍歷演算法 void BFSTraverse (MGraph G) { int i, j; int visited[50]; Queue Q; // 建立一個佇列 // 遍歷頂點 for (i = 0; i < G.numVertexes; ++i) { // 給所有頂點是否被訪問過作標誌 visited[i] = FALSE; } // 初始化佇列 initQueue( &Q ); for (i = 0; i < G.numVertexes; ++i) { // 如果沒有訪問過的頂點 if (!visited[i]) { printf("%c\n", G.vexs[i]); // 列印頂點 visited[i] = TRUE; // 將頂點昨個訪問標記 EnQueue(&Q, i); // 將此頂點插入佇列 // 如果當前佇列不為空 while( !QueueEmpty(Q)) { // 將隊中元素出佇列, 賦值給i DeQueue(&Q, &i); for (j = 0; j < G.numVertexes; ++j) { // 判斷其他頂點若與當前頂點存在邊且未訪問過 if (G.arc[i][j] == 1 && !visited[j]) { printf("%c\n", G.vexs[j]); // 列印頂點 visited[j] = TRUE; // 將頂點昨個訪問標記 EnQueue(&Q, j); // 將此頂點插入佇列 } } } } } }
相關推薦
資料結構與演算法一一圖
二、圖的儲存結構<鄰接矩陣>三、圖的儲存結構<鄰接表>四、圖的遍歷// ---------------------鄰接矩陣儲存結構------------------------
18_資料結構與演算法_圖(鄰接表)_Python實現
# Title : TODO # Objective : TODO # Created by: Chen Da # Created on: 2018/11/10 #頂點類 class Vertex(object): def __init__(self,key): s
資料結構與演算法15-圖的基本資料操作
基本資料操作 ADT 圖(Graph) Data 頂點的有窮非空集合和邊的集合 Operation CreateGraph(*G,V,VR):V點集,VR邊弧集的定義構造圖G DestroyGraph(*G)
資料結構與演算法18-圖的遍歷
從圖中某一個頂點出發訪遍圖中其餘頂點,且使每個頂點權被訪問一次,這一過程就叫做圖的遍歷(Traversing Graph)。 深度優先遍歷(Depth_First_Search) 從圖中某個頂點v出發,訪問此頂點,然後從v的未被訪問的鄰接點出發深度優先遍歷圖,直至
資料結構與演算法19-圖的最小生成樹
我們把構造連通網的最小代價生成樹稱為最小生成樹(Minimum Cost Spanning Tree) 普里姆(Prim)演算法 也就是說,現在我們已經有一個儲存結構 MGraph的G,它的arc二維陣列如圖所示。陣列中我們用65535代表∞ 於是普
資料結構與演算法22-圖的關鍵路徑
關鍵路徑 拓撲排序主要是為解決一個工程能否順序進行的問題,但有時我們還需要解決工程完成需要的最短時間問題。比如造一輛汽車,我們需要先造各種各樣零件、部件,最終再組裝成車,假如,造一個輪子需要0.5天時間,造一個發動機需要3天時間,造一個車底盤需要2天時間,造一個外殼需要2天時間,其他零部件時間需
資料結構與演算法21-圖的拓撲排序
拓撲排序 學了兩個有環的圖應用,現在我們來談談無環的圖應用。無環,即是圖中沒有迴路的意思。 拓撲排序介紹 在一個表示工作的有向圖中,用頂點表示活動,用弧表示活動之間的優先關係,這樣有向圖為頂點表示活動的網,我們稱為AOV網(Activity On&nb
資料結構與演算法20-圖的最短路徑
最短路徑 對於網圖來說,最短路徑,是指兩頂點之間經過的邊上權值之和最少的路徑,並且我們稱路徑上的第一個頂點是源點,最後一個頂點是終點。 迪傑斯特拉演算法 它並不是一下子就求出V0到V8的最短路徑,而一步步求出它們之間頂點的最短路徑,過程中都是基於已經求出的最短路徑
資料結構與演算法17-圖的十字連結串列
對於有向圖來說,鄰接表是有缺陷的,關心了出度問題,想了解入度就必須要遍歷整個圖才能知道,反之,逆鄰接表解決了入度的情況。 把鄰接表與逆鄰接表結合起來,即有向圖的一種儲存方法十字連結串列(Orthogonal List)。 我們重新定義頂點表結構 firsti
資料結構與演算法16-圖的儲存結構
圖的儲存結構 圖的儲存結構相較線性表與樹來說就更加複雜了。首先,我們口頭上說的“頂點的位置”或“鄰接點的位置”只是一個相對的概念。其實從圖的邏輯結構定義來看,圖上任何一個頂點都可被看成是第一個頂點,任一頂點的鄰接點之間也不存在次序關係。如下圖 用之前學過的資料結構來表
Javascript之資料結構與演算法的圖(Graph)實現
Javascript之資料結構與演算法的圖(Graph)實現 簡介 廣度優先搜尋演算法實際應用-最短路徑(非權值) 深度優先搜尋演算法實際應用-拓撲排序(有向無環圖) Dijkstra 演算法 Floyd-Warshall
資料結構與演算法一一遞迴操作
一、斐波那契數列// 迭代實現 void iterationFib() { int a[10] = {1, 1}; int len = sizeof(a) / sizeof(int); print
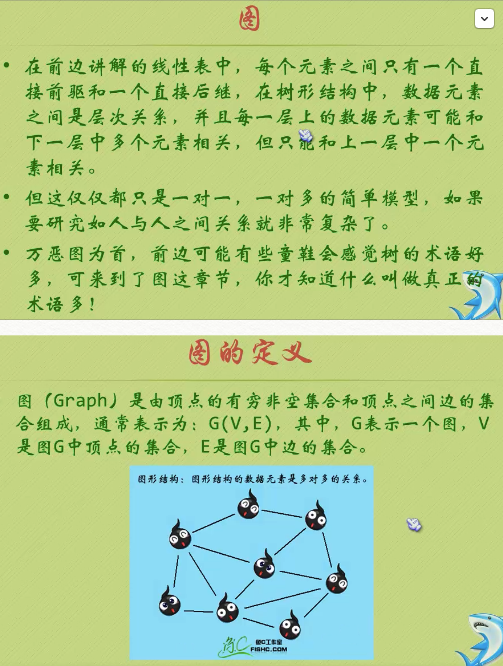
【資料結構與演算法】圖
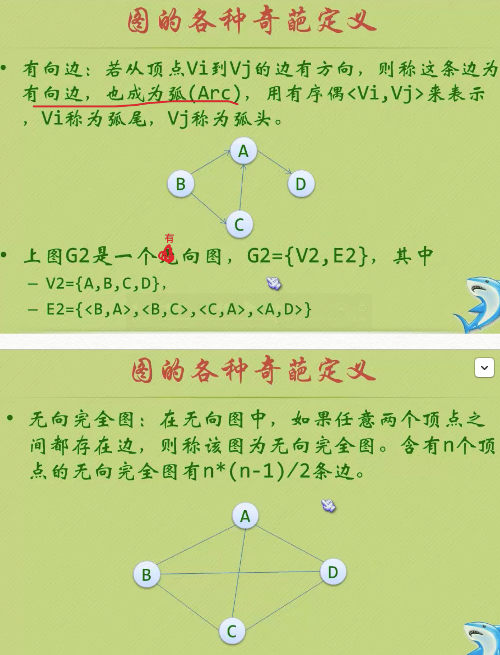
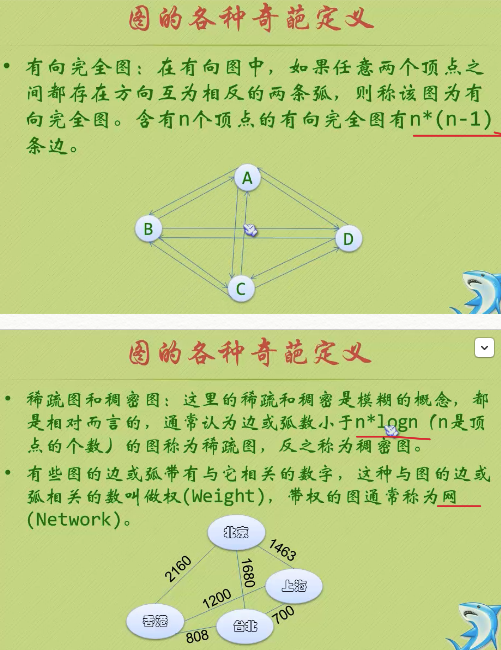
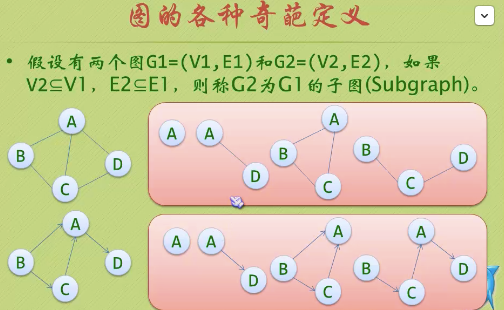
一、概念 定義: 圖由點集合和邊集合組成,記做G=(V,E),其中點集合不能為空且應該有窮,邊集合可以為空。 ①有向圖:邊有方向,用<Vi,Vj>表示 ②
(c++)資料結構與演算法之圖:鄰接矩陣、深度廣度遍歷、構造最小生成樹(prim、kruskal演算法)
//圖的鄰接矩陣實現 //廣度遍歷bfs和深度遍歷dfs //構造最小生成樹的prim、kruskal演算法 #include <iostream> #include<stack> #include<queue> #define WEI
資料結構與演算法之圖計算
圖演算法,在實際的程式設計中還是會經常遇到的,最主要的就是兩種圖的遍歷演算法。舉個例子,Java程式設計師必須掌握的垃圾回收(Garbage Collection,GC)裡面,就非常依賴圖演算法。所以,
《資料結構與演算法那》第七次 廣度、深度優先遍歷 圖及圖的遍歷(下)
《資料結構與演算法那》第七次課實驗內容 圖及圖的遍歷(下) 實驗目的: 熟悉圖的兩種儲存結構:鄰接矩陣和鄰接連結串列。 掌握在圖的鄰接表儲存結構上的遍歷演算法的實現。 實驗內容: 在已經開發好的c++類adjacencyGraph中,新增兩個成員函式,B
《資料結構與演算法》第六次 圖及圖的遍歷(上)
《資料結構與演算法那》第六次課實驗內容 圖及圖的遍歷(上) 實驗目的: 熟悉圖的兩種儲存結構:鄰接矩陣和鄰接連結串列。 掌握在圖的鄰接表儲存結構上的遍歷演算法的實現。 實驗內容: 開發c++類adjacencyGraph,用鄰接矩陣描述一個無向圖,要求可
資料結構與演算法——有向圖鄰接表輸出其拓撲排序序列
測試資料 輸入: 12 16 c1 c2 c3 c4 c5 c6 c7 c8 c9 c10 c11 c12 c1 c4 c1 c2 c1 c3 c1 c12 c4 c5 c2 c3 c3 c5 c3 c7 c5 c7 c3 c8 c9 c12 c9 c10 c10 c12 c
《資料結構與演算法設計》實驗報告書之圖的遍歷操作
《資料結構與演算法設計》實驗報告書之圖的遍歷操作 實驗專案 圖的遍歷操作 實驗目的 掌握有向圖和無向圖的概念;掌握鄰接矩陣和鄰接連結串列建立圖的儲存結構;掌握DFS及BFS對圖的遍歷操作;瞭解圖結構在人工智慧、工程等領域的廣泛應用。 實驗內容 採用鄰接矩陣和鄰接連結串列其中一種作
為什麼我要放棄javaScript資料結構與演算法(第九章)—— 圖
本章中,將學習另外一種非線性資料結構——圖。這是學習的最後一種資料結構,後面將學習排序和搜尋演算法。 第九章 圖 圖的相關術語 圖是網路結構的抽象模型。圖是一組由邊連線的節點(或頂點)。學習圖是重要的,因為在任何二元關係都可以用圖來表示。 任何社交網路都可以用圖來表示。 我們還可以用圖來表示道路、航班以及通訊