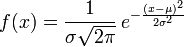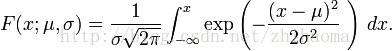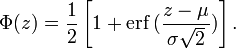高斯分佈的一些理解
轉自:http://blog.csdn.net/rns521/article/details/6953591
正態分佈(Normal distribution)又名高斯分佈(Gaussian distribution),是一個在數學、物理及工程等領域都非常重要的概率分佈,在統計學的許多方面有著重大的影響力。
若隨機變數X服從一個數學期望為μ、標準方差為σ2的高斯分佈,記為:X∼N(μ,σ²),
則其概率密度函式為:
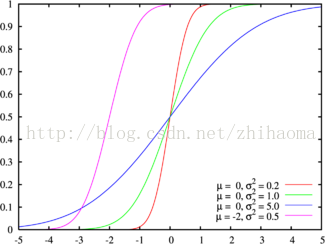
正態分佈的期望值μ決定了其位置,其標準差σ決定了分佈的幅度。因其曲線呈鐘形,因此人們又經常稱之為鐘形曲線。我們通常所說的標準正態分佈是μ = 0,σ = 1的正態分佈。
正態分佈的定義
有幾種不同的方法用來說明一個隨機變數。最直觀的方法是概率密度函式,這種方法能夠表示隨機變數每個取值有多大的可能性。累積分佈函式是一種概率上更加清楚的方法,但是非專業人士看起來不直觀(請看下邊的例子)。還有一些其他的等價方法,例如cumulant、特徵函式、動差生成函式以及cumulant-生成函式。這些方法中有一些對於理論工作非常有用,但是不夠直觀。請參考關於概率分佈的討論。
概率密度函式
正態分佈的概率密度函式均值為μ 方差為σ² (或標準差σ)是高斯函式的一個例項:
下邊是給出了不同引數的正態分佈的函式圖:
正態分佈中一些值得注意的量:
- 密度函式關於平均值對稱
- 平均值是它的眾數(statistical mode)以及中位數(median)
- 函式曲線下68.268949%的面積在平均值左右的一個標準差範圍內
- 95.449974%的面積在平均值左右兩個標準差2σ的範圍內
- 99.730020%的面積在平均值左右三個標準差3σ的範圍內
- 99.993666%的面積在平均值左右四個標準差4σ的範圍內
- 反曲點(inflection point)在離平均值的距離為標準差之處
累積分佈函式
累積分佈函式是指隨機變數X小於或等於x的概率,用密度函式表示為
正態分佈的累積分佈函式能夠由一個叫做誤差函式的特殊函式表示:
正態分佈的一些性質
1、如果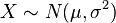 且a與b是實數,那麼aX+b ∼N(aμ+b,(aσ)²)
且a與b是實數,那麼aX+b ∼N(aμ+b,(aσ)²)
2、如果 與
與 是統計獨立的正態分佈隨機變數,那麼:
是統計獨立的正態分佈隨機變數,那麼:
- 它們的和也滿足正態分佈
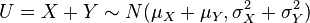
- 它們的差也滿足正態分佈

- U和V兩者是相互獨立的。
3、如果 和
和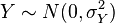 是獨立正態隨機變數,那麼:
是獨立正態隨機變數,那麼:
- 它們的積XY服從概率密度函式為p的分佈
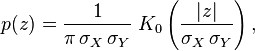 其中K0是貝塞爾函式(modified Bessel function)
其中K0是貝塞爾函式(modified Bessel function)
- 它們的比符合柯西分佈,滿足X / Y∼Cauchy(0,σX / σY)。
4、 為獨立標準正態隨機變數,那麼
為獨立標準正態隨機變數,那麼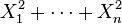 服從自由度為n的卡方分佈。
服從自由度為n的卡方分佈。
相關分佈:
- R∼Rayleigh(σ)是瑞利分佈,如果
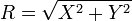 ,這裡X∼N(0,σ2)和Y∼N(0,σ2)是兩個獨立正態分佈。
,這裡X∼N(0,σ2)和Y∼N(0,σ2)是兩個獨立正態分佈。  是卡方分佈具有ν自由度,如果
是卡方分佈具有ν自由度,如果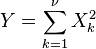 這裡Xk∼N(0,1)其中
這裡Xk∼N(0,1)其中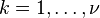 是獨立的。
是獨立的。- Y∼Cauchy(μ = 0,θ = 1)是柯西分佈,如果Y = X1 / X2,其中X1∼N(0,1)並且X2∼N(0,1)是兩個獨立的正態分佈。
- Y∼Log-N(μ,σ2)是對數正態分佈如果Y = eX並且X∼N(μ,σ2).
- 與Lévy skew alpha-stable分佈相關:如果
 因而
因而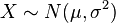 .
. - 截斷正態分佈.如果
 , 在A以下和B以上擷取X 將產生一個平均值
, 在A以下和B以上擷取X 將產生一個平均值 這裡
這裡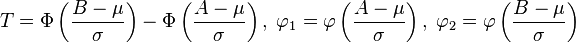 ,φ是一個標準正態隨機變數的密度函式
,φ是一個標準正態隨機變數的密度函式 - 如果X是一個正態分佈的隨機變數, Y = | X | ,那麼Y具有摺疊正態分佈.