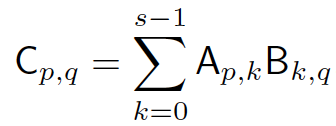序列實現

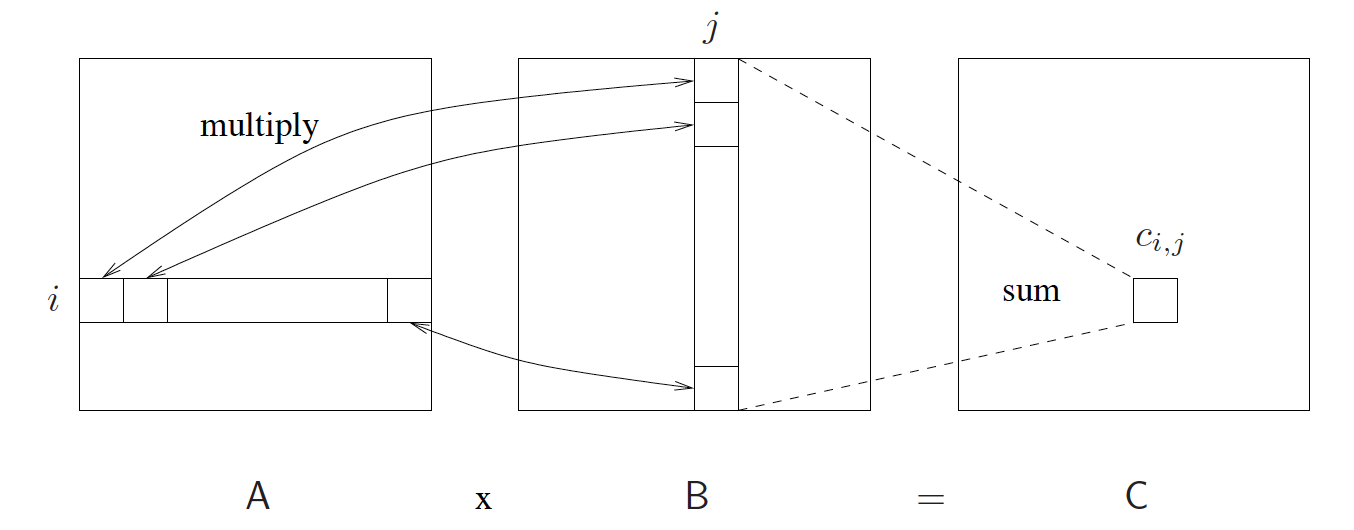
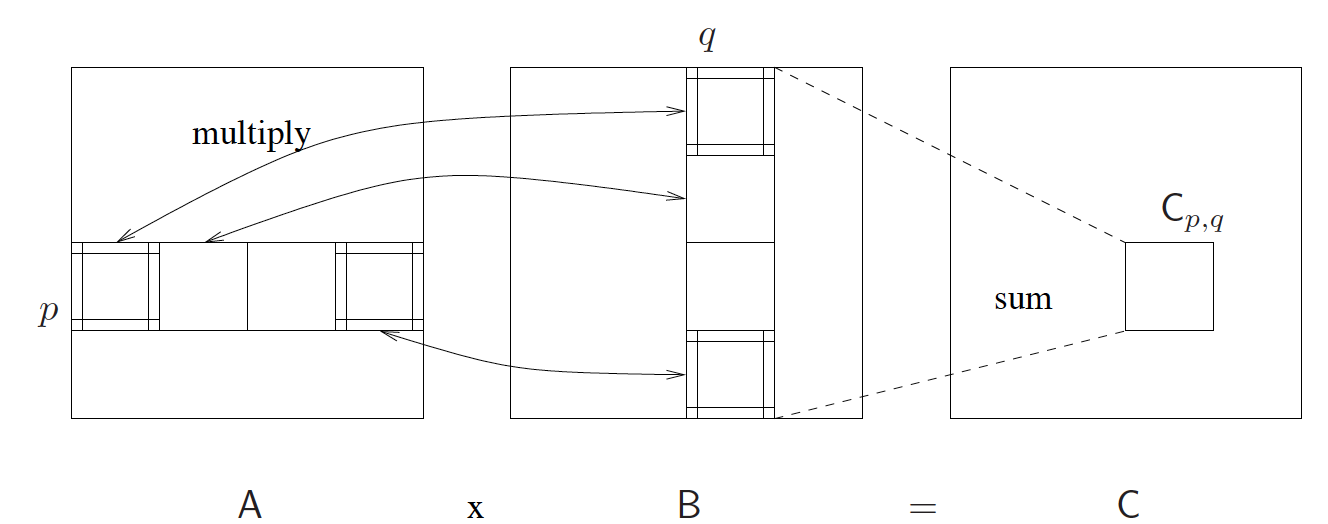
根據線性代數的基本知識，m × l 的矩陣A，乘以一個大小為 l × n 的矩陣B，將得到一個 m × n 的矩陣C=A×B，其中

下圖是用圖示來表示的這種計算規則：

為了方便討論，我們可以不是普遍性地假設有所矩陣的大小都是 n × n 的，下面就是序列實現的矩陣乘法的程式碼：

int A[n][n], B[n][n], C[n][n];
...
for(i=0;i<n;i++){
    for(j=0;j<n;j++){
        C[i][j]=0;
        for(k=0;k<n;k++)
            C[i][j]+=A[i][k]*B[k][j];
    }
}
 

基本並行實現的討論

正如前面所講的，矩陣相乘過程中，結果矩陣C中的每個元素都是可以獨立計算的，即彼此之間並無依賴性。所以如果採用更多的處理器，將會顯著地提高矩陣相乘的計算效率。

對於大小為n × n 的矩陣，加入我們有n個處理器，那麼結果矩陣中的每一行，都可以用一個處理器來負責計算。此時，總共的平行計算步數為 O(n^2)。你可以理解為在序列實現的程式碼中，最外層的迴圈 for(i=0;i<n;i++) 被分別由n個處理器來並行的執行，而每個處理需要完成的任務僅僅是內部的兩層迴圈。

如果採用n^2個處理器，那麼就相當於結果矩陣中的每個元素都由一個處理器來負責計算。此時，總共的平行計算步數為 O(n)。你可以理解為在序列實現的程式碼中，最外面的兩層迴圈 被分解到n^2個處理器來並行的執行，而每個處理需要完成的任務僅僅是內部的一層迴圈，即for(k=0;k<n;k++)。

更進一步，如果有n^3個處理器，那麼即使最內層的迴圈for(k=0;k<n;k++)也有n個處理器在並行的負責。但是最終的求和運算，我們需要一個類似reduction的操作，因此最終的計算複雜度就是O(log n)。

當然，你一定會想到的是，實際中，通常並不可能有像矩陣元素那麼多的處理器資源。這時我們該怎麼做。對於一個大小為n × n 的大矩陣A，我們其實可以把它切分成s^2個子矩陣A_p,q，每個子矩陣的大小為 m × m，其中 m = n / s，即0 <= p, q < s。對於兩個大矩陣A和B，現在我們有：

用圖示表示則有：

Cannon演算法

著名的Cannnon演算法使用一個由s^2

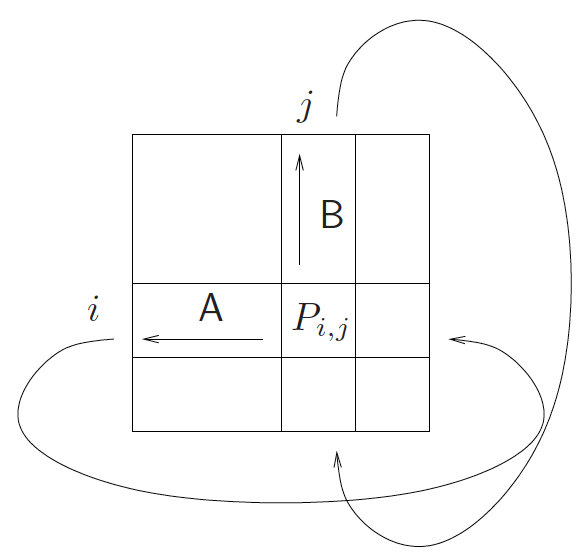
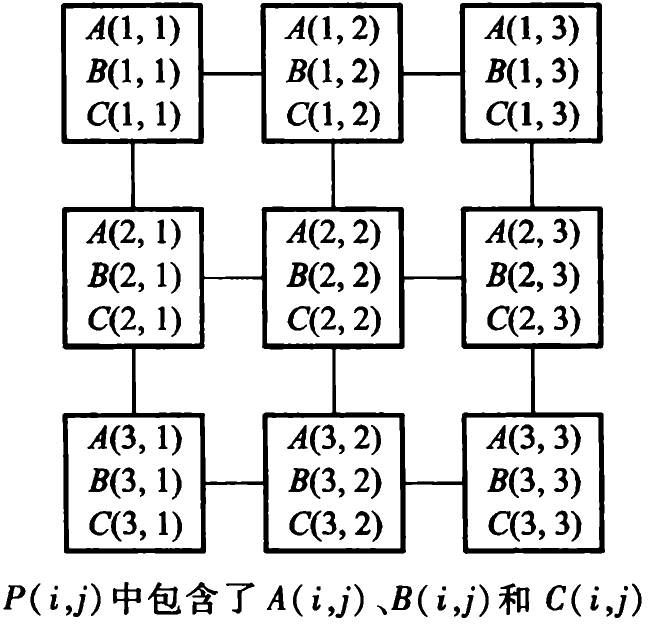
這個演算法的根本出發點是在處理器陣列中，要合理分佈兩個待乘的矩陣元素。由乘積公式可知，要在處理單元 P(i,j)中計算乘積元素C(i,j)，必須在該單元中準備好矩陣元素A(i,s)和B(s,j)。但是如果我們像下圖那樣分佈矩陣元素，我們在計算C(i,j)時所需的元素顯然是不足夠的，但是可以通過向上迴圈位移B的元素，並向左迴圈位移A的元素，來獲取合適的成對的矩陣元素。

Cannnon演算法的具體流程：

下面是矩陣位移的一個示例，其中s=3；

顯然，演算法的複雜度 t(n)=O(n)， p(n) = n^2，w(n) = O(n^3)，所以是成本最佳的。

---------------------------------------------

參考文獻與推薦閱讀材料

【1】陳國良，並行演算法的設計與分析（第3版），高等教育出版社，2009

【2】矩陣計算並行演算法（百度文庫地址：http://wenku.baidu.com/view/d64ba9b4b14e852458fb57fc.html）

（本文完）