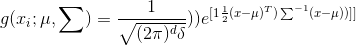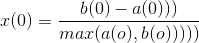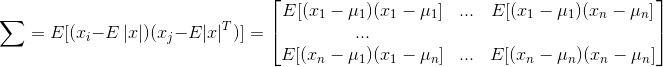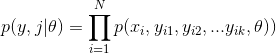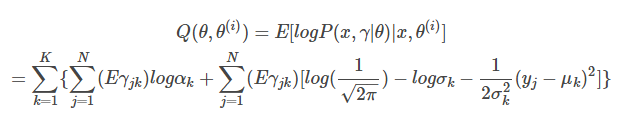機器學習中的聚類
1、聚類
無監督通過對無標記訓練樣本的學習來找到這些資料的內在性質,使用最多的就是聚類。
聚類思想:將資料劃分為幾個不相交的子集(也就是簇,cluster),每個簇潛在的對應某一個概念。聚類僅僅是生成cluster,但是簇的語義要由使用者自己解釋。
聚類的作用:探索性方法,用來分析內在特點,尋找資料的分佈規律。
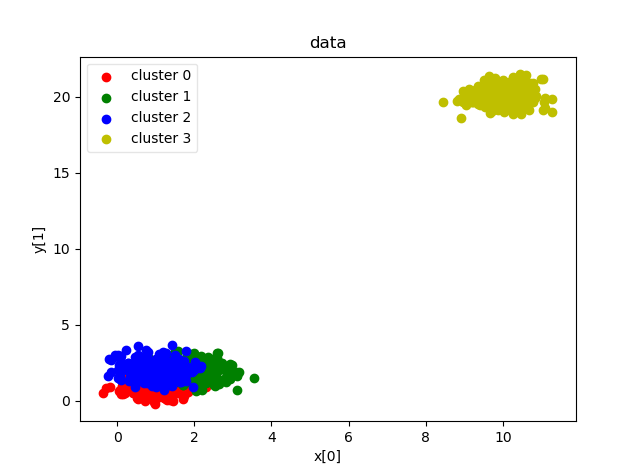
如圖樣本點分為四個簇
2、聚類的方法
(1)k-means
即xi裡那個簇均值向量最近,該樣本就標記為那個簇
工作流程:隨機選取k個初始點作為質心,然後將每一個點分配到離質心最近的那個簇中,完成後,每個簇的質心更改為該簇所有點的平均值
引數k:該演算法需要確定引數k,常用的方法有如下:
- 經驗:使用公式k=sqrt(n/2),不過這種做法以及公式沒有數學的依據
- 肘方法:離差平方和變化最快的地方對應的簇較為合理
- PSF(偽F演算法)和PSTZ(偽T演算法)
- 交叉驗證
缺點:結果的好壞決定於初始聚類中心的選擇,容易陷入區域性最優解,對k的選擇沒有準則
(2)高斯混合模型(GMM)
高斯混合模型是那些點的概率密度函式
其中u是密度中心點,常用樣本的均值,∑是協方差矩陣
缺點:當樣本在空間中的分佈不是橢球狀時,模型增多,需要確定的引數就增加
(3)密度聚類(DBSCAN)
目的就是為了過濾低密度的區域
演算法思想:若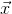
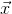
(4)層次聚類(AGNES)
不同層次的進行劃分
演算法思想:將每個物件看成一個簇,根據某些準則,一步步合併知道預設的聚類簇的個數
2、聚類涉及的問題
(1)聚類的趨勢
用於聚類的資料不可均勻分佈,但是如果資料多且複雜,我們用人眼無法判別是否適合聚類的時候,可以用霍普金斯統計量來檢驗空間的隨機性。
霍普金斯步驟:
- 從D空間中均勻獲點p1~pn,
,點p可以不是樣本點
- 從D中均勻獲取點q1~qn,
,點q是樣本點
如果不是均勻分佈的話,yi一般會比xi小,因為yi是取樣本中的點,距離一般會比樣本外的點距離小,當樣本是均勻分佈的時候,H是接近0.5,不適合用聚類,聚類的高度越傾斜,yi會遠小於xi,這時候H會接近於0
(2)評估聚類的質量
- 外在方法:它是有基準的
Oi樣本,Oj基準,當L(Oi)=L(Oj) ∩ C(Oi)=C(Oj)的時候,c=1,也就是在基準和聚類中兩個分類都相等
- 內在方法:輪廓係數,很多情況下我們是沒有基準的,這時候用輪廓係數來衡量聚類的質量
選擇一個類的平均數,a(0)為該類中任意一點到平均數的距離,b(0)表示其他類別到該平均數的距離
當x(0)接近1的時候,說明該模型是緊湊的,當x(0)為負數的時候,該模型是不可取的
(3)GMM中的∑(協方差矩陣)
(4)EM演算法
EM演算法是聚類中常用的方法,K-means,GMM等都用到了EM演算法
EM演算法分為兩步,每次迭代由這兩部分組成:
- E算期望值,就是求Q函式的期望,其中Q函式是收斂的
- M極大化引數,用了極大似然估計法
演算法過程:
- 對於似然函式
,求它的對數似然函式(其中x資料集在公式中是已知的,但是他來自那個模型我們卻是未知的,用
,1表示第i個觀測來自第k個分模型,
- E確定Q,求期望
- M用極大似然估計法得出θ