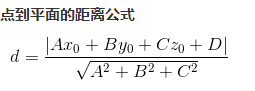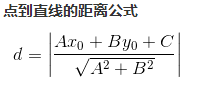第六章 支援向量機

6.1 什麼是支援向量機

支援向量機(Support Vector Machines)是目前被認為最好的現成的演算法之一

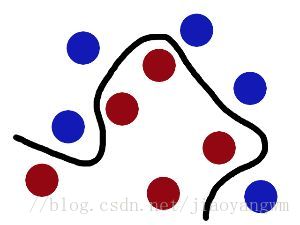
在很久以前的情人節，大俠要去救他的愛人，但魔鬼和他玩了一個遊戲。

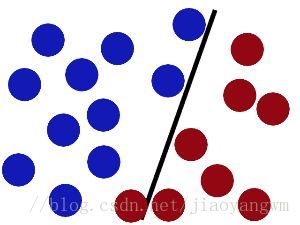
魔鬼在桌子上似乎有規律放了兩種顏色的球，說：“你用一根棍分開它們？要求：儘量在放更多球之後，仍然適用。”

於是大俠這樣放，乾的不錯？

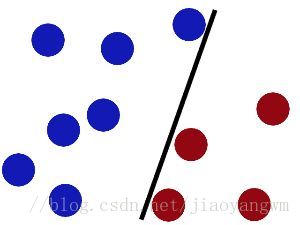
然後魔鬼，又在桌上放了更多的球，似乎有一個球站錯了陣營。

SVM就是試圖把棍放在最佳位置，好讓在棍的兩邊有儘可能大的間隙。

現在即使魔鬼放了更多的球，棍仍然是一個好的分界線。

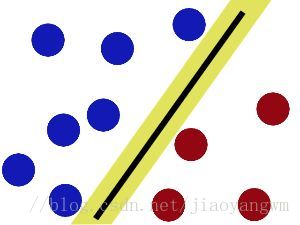
然後，在SVM 工具箱中有另一個更加重要的 trick。 魔鬼看到大俠已經學會了一個trick，於是魔鬼給了大俠一個新的挑戰。

現在，大俠沒有棍可以很好幫他分開兩種球了，現在怎麼辦呢？當然像所有武俠片中一樣大俠桌子一拍，球飛到空中。然後，憑藉大俠的輕功，大俠抓起一張紙，插到了兩種球的中間。

現在，從魔鬼的角度看這些球，這些球看起來像是被一條曲線分開了。

再之後，無聊的大人們，把這些球叫做 「data」，把棍子 叫做 「classifier」, 最大間隙trick 叫做「optimization」， 拍桌子叫做「kernelling」, 那張紙叫做「hyperplane」。

當資料為線性可分的時候，也就是可以用一根棍子將兩種小球分開的時候，只要將棍子放在讓小球距離棍子的距離最大化的位置即可，尋找該最大間隔的過程就叫做最優化。

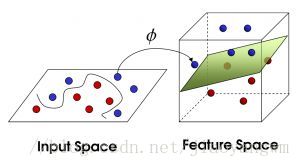
但是一般的資料是線性不可分的，所以要將其轉化到高維空間去，用一張紙將其進行分類，空間轉化就是需要核函式，用於切分小球的紙就是超平面。

什麼是SVM：

分類作為資料探勘領域中一項非常重要的任務，它的目的是學會一個分類函式或分類模型(或者叫做分類器)，而支援向量機本身便是一種監督式學習的方法(至於具體什麼是監督學習與非監督學習，請參見此係列Machine L&Data Mining第一篇)，它廣泛的應用於統計分類以及迴歸分析中。

支援向量機（SVM）是90年代中期發展起來的基於統計學習理論的一種機器學習方法，通過尋求結構化風險最小來提高學習機泛化能力，實現經驗風險和置信範圍的最小化，從而達到在統計樣本量較少的情況下，亦能獲得良好統計規律的目的。

通俗來講，它是一種二類分類模型，其基本模型定義為特徵空間上的間隔最大的線性分類器，即支援向量機的學習策略便是間隔最大化，最終可轉化為一個凸二次規劃問題的求解。

6.1.1 線性SVM

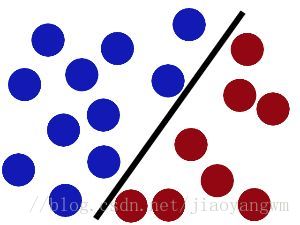
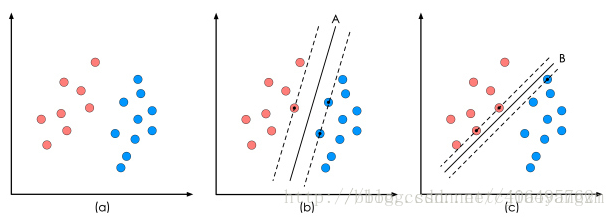
線性可分的二分類問題：

上圖中紅色和藍色分別表示不同的兩個類別，資料為線性可分，但是將其分開的直線不止一條，(b)(c)分別給出了不同的方法。黑色的實現為“決策面”，每個決策面對應一個線性分類器，兩者的效能是有差距的。

決策面不同的情況下，新增一個紅色的點，顯然(b)仍然能夠很好的分類，但是(c)已經分類錯誤了，所以決策面(b)優於(c)。

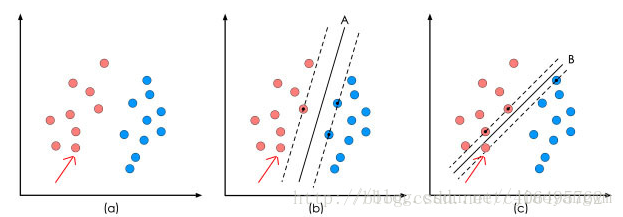
如何選擇較好的決策面：

在保證決策面方向不變且不會出現錯分樣本的情況下移動決策面，會在原來的決策面兩側找到兩個極限位置（越過該位置就會產生錯分現象），如虛線所示。

虛線的位置由決策面的方向和距離原決策面最近的幾個樣本的位置決定。而這兩條平行虛線正中間的分界線就是在保持當前決策面方向不變的前提下的最優決策面。

兩條虛線之間的垂直距離就是這個最優決策面對應的分類間隔。顯然每一個可能把資料集正確分開的方向都有一個最優決策面（有些方向無論如何移動決策面的位置也不可能將兩類樣本完全分開），而不同方向的最優決策面的分類間隔通常是不同的，那個具有“最大間隔”的決策面就是SVM要尋找的最優解。

而這個真正的最優解對應的兩側虛線所穿過的樣本點，就是SVM中的支援樣本點，稱為”支援向量”。

學習的目標是在特徵空間中找到一個分離超平面，能將例項分到不同的類中。

分離超平面的方程：w⋅x+b=0 $w\cdot x+b=0$

方程由法向量w $w$和截距b $b$決定，可以用(w,b) $(w,b)$來表示。

分離超平面將特徵空間劃分為兩部分，一部分為正類，一部分為負類，法向量指向的一側為正類，另一側為負類。

6.1.2 函式間隔和幾何間隔

備註：

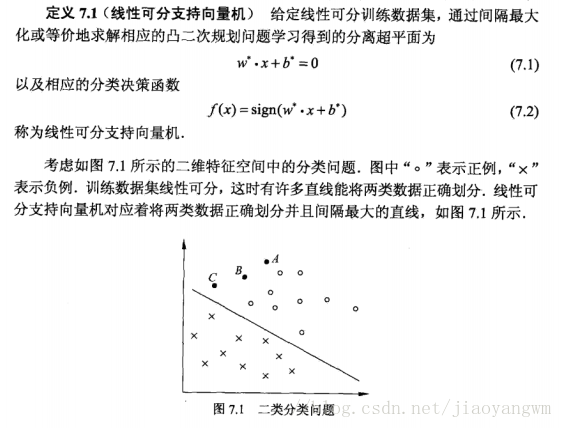
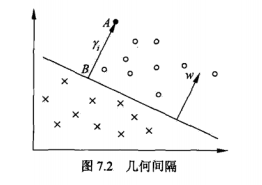
上圖7.1中有A,B,C三個點，表示3個例項，均在分離超平面的正類一側，預測他們的類，點A距離超平面較遠，若預測該類為正類，就比較確信為正確的，點C距離分離超平面較近，不是很確信。

函式間隔（function margin）：

一般來說，一個點距離分離超平面的遠近可以表示分類預測的確信程度，在超平面w⋅x+b=0 $w\cdot x+b=0$確定的情況下，|w⋅x+b| $|w\cdot x+b|$能夠相對的表示點x距離超平面的遠近，而w⋅x+b $w\cdot x+b$的符號與類標記y的符號是否一致能夠表示分類是否正確，所以可以量y(w⋅x+b) $y(w\cdot x+b)$來表示分離的正確性和確信度。

從函式間隔變為幾何間隔：

雖然函式間隔可以表示分類預測的正確性即確信度，但是選擇分離超平面時，只有函式間隔遠遠不夠，因為只要成比例的改變w $w$和b $b$，例如將它們改變為2w $2w$和2b $2b$，超平面並沒有改變（w∗x+b=0 $w\ast x+b=0$，右邊為0，不會因為係數而改變），但是函式間隔（y(w∗x+b) $y(w\ast x+b)$）卻變為原來的2倍。

對分離超平面的法向量w $w$加某些約束，如規範化，||w||=1 $||w||=1$，使得間隔是確定的，此時函式間隔變為幾何間隔。

上圖給出了超平面(w,b) $(w,b)$和其法向量w $w$，點A $A$表示某一例項x i  $x_i$，其類標記為y i =+1 $y_i=+1$，點A $A$與超平面的距離由線段AB $AB$給出，記作y i  $y_i$：

y i =w||w||⋅x i +b||w|| $y_i=\frac{w}{||w||}\cdot x_i+\frac{b}{||w||}$

其中，||w|| $||w||$為w $w$的L 2  $L_2$範數，如果點A $A$在超平面的負一側，即y i =−1 $y_i=-1$，則：

y i =−(w||w||⋅b||w||) $y_i=-\left(\frac{w}{||w||}\cdot \frac{b}{||w||}\right)$

一般情況，當樣本點