--------韋訪 20181114

1、概述

繼續學習，支援向量機在傳統的機器學習的地位還是很高的，不過，現在風頭已經被神經網路蓋過了，但是，還是得學習的。

2、概念

先來看一下，為什麼需要支援向量機？

 如上圖所示，這是一個二分類問題，有三條直線，都能將紅點和黃點分開，那麼，哪條直線更優？

直觀上看，中間的那條直線應該是最優的，因為另外兩條直線都更接近樣本的邊界。用另一張圖來更直觀的看應該怎麼求這條最優分界線。

如上圖所示，左右兩張圖的直線都能將樣本分類，直線旁邊的兩條虛線是與直線平行的，如果將兩條虛線之間的距離看做容錯率的話，顯然右邊那條直線的容錯率是更好的，也就是更魯棒，泛化能力更強。

3、距離公式

那這條直線應該怎麼求呢？

既然遠離樣本邊界的直線更好，是不是應該先找到離直線最近的樣本，然後離它越遠越好就行了？如上圖所示，先找到離直線最近的樣本點，然後，遠離它。

這樣我們就將問題轉成了求“距離”的問題了。

在真實的分類任務中，樣本可能不會剛好分佈在二維平面上，有可能是多維的超平面上。在樣本空間中，任何一個超平面都可以用如下方程表示，

WΤx+b=0

其中，W為法向量，決定超平面的方向，b為偏置項，決定超平面與原點之間的距離。

如上圖所示，假設陰影部分的平面是我們的劃分超平面，x是樣本點，我們要求的就是x到劃分超平面的距離。直接求距離可能不太好求，我們就間接來求。

在平面上隨意找到兩個點x`和x``，這兩點組成一個向量，因為這兩點在平面上，所以它滿足公式，WΤx+b=0，分別將它們帶入公式，得

WΤx`=-b, WΤx``=-b

因為法向量與x到平面距離的直線是平行的，所以，我們可以先求x到x`的距離d`，然後再求d`到法向量上的投影，就是我們要求的點x到平面上的距離了，距離公式如下，

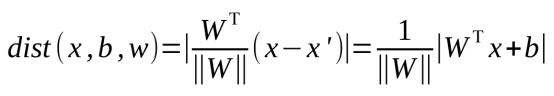
4、資料標籤定義

假設超平面能將訓練樣本正確的分類，則在資料集中，yi為樣本類別，若yi=+1，則有wΤxi+b>0，若yi=-1，則有wΤxi+b<0。如果我們將決策方程表示為，

 

則有，

將上面兩式帶入距離公式，得，

 

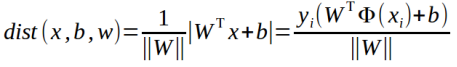
1. 目標函式

對於決策方程(w, b)，可以通過縮放使得其結果值|y|≥1，為什麼能這麼縮放呢？上面的式子，，讓它左邊和右邊同時乘以一個值，等式還是成立的吧？那麼總有一個值可以使得等式左邊的大於1吧。帶入，可以得到下式，

 前面說過了，我們的目的是求離劃分超平面最近的樣本點，然後，遠離它，那麼，得到的目標函式應該如下，

由於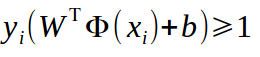，所以，我們只需要考慮，

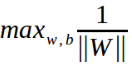即可。

求極大值？我們以前的做法都是將它轉變成求極小值的計算，求分數的極大值，不就是求分母的極小值嗎？所以，可以將上式求極大值的問題轉成下式，求極小值，

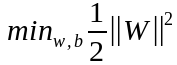
 別忘了，上式成立還有一個約束條件，

上面兩式就是支援向量機的基本型。

6、拉格朗日乘子法

在繼續求解SVM之前，先來說說拉格朗日乘子法，拉格朗日乘子法是一種尋找多元函式在一組約束下的極值方法。通過引入拉格朗日乘子，可以將有d個變數與k個約束條件的最優化問題轉化為具有d+k個變數的無約束優化問題求解。

等式約束g(x)=0優化問題：
假定x為d維向量，現在尋找x的某個取值x*，使得目標函式f(x)最小，且同時滿足g(x)=0的約束條件。

從幾何的角度看，這個問題的目標是在方程g(x)=0確定的d-1維曲面上尋找使得目標函式f(x)最小化的點。由此可得，

1. 對於約束曲面上的任意點x，該點的梯度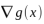正交於約束曲面。
2. 在最優點x*，目標函式在該點的梯度正交於約束曲面。

如下圖所示，

梯度和的方向必相同或者相反，則存在λ≠0，使得，

其中，λ稱為拉格朗日乘子，拉格朗日函式如下，

不等式約束g(x)≤0優化問題：

如上圖所示，此時最優點x*在g(x)<0區域中，或者在g(x)=0邊界上，

1. 當x*在g(x)<0區域中，直接極小化f(x)即可。
2. 當x*在g(x)=0上，則等價於上面的等式約束優化問題。需要注意的是，此時，和的方向必須相反，則存在常數λ>0使得.

整合這兩種情形，必須滿足λg(x)=0，因此可以將在約束條件g(x)≤0下最小化f(x)，轉化為在如下約束條件下，最小化拉格朗日函式，

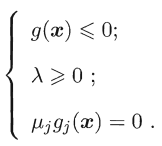
上面的條件稱為KKT條件。

上面的做法可以推廣到多個約束，假設有m個等式約束和n個不等式約束，且可行域D非空的優化問題，

引入拉格朗日乘子λ=(λ1,λ2...λm)Τ和μ=(μ1,μ2...μn)Τ，相應的拉格朗日函式為，

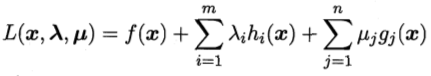
約束條件KKT為，

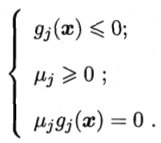
7、求解SVM

將

帶入拉格朗日函式

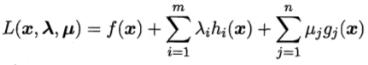
得，

另對w和b的偏導為0，

對w求偏導：

對b求偏導：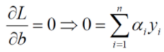

再將上面的式子帶入原式，就可以將w和b消去，

 

由於對偶性質，

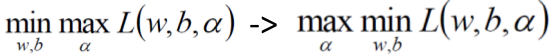
上面完成了第一步，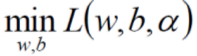

現在我們繼續對α求極大值，

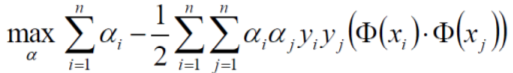
求極大值，我們又可以將它轉成求極小值，

 

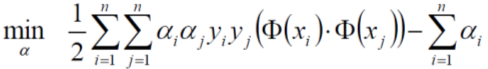
 別忘了上式成立是有條件的，

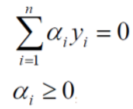
然後，解出α，根據下式再求出w和b，即可得到模型

8、求解SVM例項

下面，用一個例項來看看怎麼用上式對SVM求解。

如上圖所示，我們有三個資料，其中，正例x1(3, 3)、x2(4, 3)，負例x3(1, 1)。

將這些資料帶到式子，

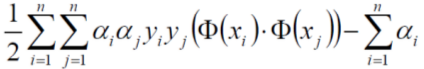
其中，約束條件為，

因為我們已經有真實的資料了，所以，約束條件也就可以寫成如下，

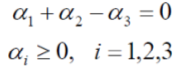
帶入資料以後，原式子為，

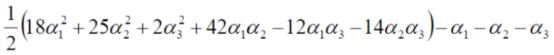
又因為，，所以可以將α3消去，上式簡化為，

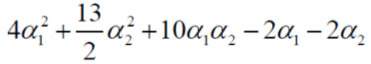
求極小值怎麼辦？求偏導唄，分別對α1和α2求偏導，令偏導等於0，可得，

因為用的是ubuntu自帶的公式編輯軟體，我不知道怎麼編輯方程組，大家知道上面兩式是方程組就好了，對上面方程組求解，得，

α1=1.5，α2=-1，這個結果並不滿足我們的約束條件αi≥0，i=1,2,3

所以我們的解應該是在邊界上，分別令α1和α2等於0，帶入，得，

α1=0，α2=-2/13

α1=0.25，α2=0

上面兩個結果中，第一個結果因為α2<0，還是不符合約束條件，而第二個結果剛好符合約束條件。又因為

所以，結果為α1=0.25，α2=0，α3=0.25 ，所以最小值在(0.25, 0, 0.25)處。

然後，將上面α的值帶入下面式子，求解w，

，得

得到w後，再根據下式求出b，

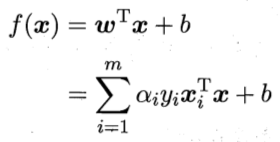
將x1的資料帶入上式，得，

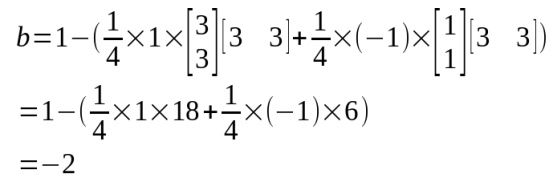
所以，最後得到的平面方程為，

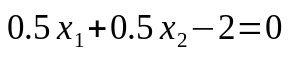
 有沒有發現，在上面這個例子中，我們最終得到的模型方程其實跟點x2(4,3)沒有關係，也就是說，如果求得的αi=0，則該樣本對f(x)沒有任何影響。也就是真正發揮作用的樣本，是α不為0的樣本點。

9、鬆弛因子

如上圖所示，有時候資料中存在一些噪音點，如果我們也將它們考慮進去了，可能得到的線就不太好了。這是因為我們的方法要求把兩個類別完全分開，這時候我們可以適當的放鬆要求，引入鬆弛因子來解決這個問題。

 

所以我們新的目標函式變成了這樣，

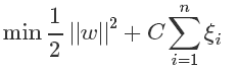
當C很大時，意味著分類嚴格

當C很小時，意味著有更大的錯誤容忍度

C是我們要指定的一個引數。

10、核函式

現實任務中，樣本空間內可能不存在一個能正確劃分兩類樣本的超平面，對於這樣的問題，我們可以將原始的樣本空間對映到一個更高維的特徵空間，使得樣本在這個特徵空間內線性可分，如下圖所示。

如果原始空間是有限維，即屬性數有限，那麼一定存在一個高維特徵空間使樣本可分。

我們令Φ(x)表示將x對映後的特徵向量，於是，在特徵空間中劃分超平面所對應的模型可表示為，

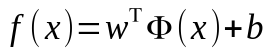
其中，w和b是模型引數，跟上面講的一樣，於是有，

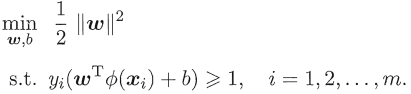
其對偶問題是，

約束條件為，

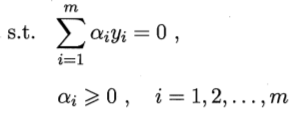
上式中，涉及到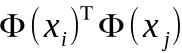的計算，這是樣本xi和xj對映到特徵空間後的內積，因為特徵空間的維數很高，甚至是無窮維，所以，直接計算的難道非常大，為避開這個障礙，設想有這樣一個函式，

即xi和xj在特徵空間的內積是它們在原始樣本空間中通過函式k(.,.)計算的結果。於是，重寫式子為，

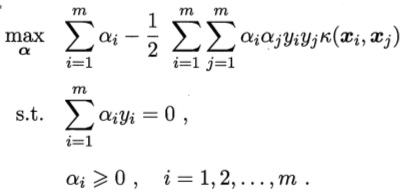
 求解後得，

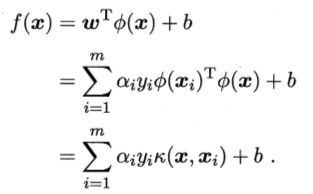
其中，函式k(.,.)就是核函式。

核函式定理：令x為輸入空間，函式k(.,.)是定義在x×x上的對稱函式，則k是核函式當且僅當對於任意資料D={x1,x2,,,xm}，核矩陣K總是半正定的。

上面定理表明，只要一個對稱函式所對應的核矩陣是半正定，它就能作為核函式使用。

上面的定理是什麼鬼，不是我們研究的重點，下面列出常用核函式，

此外，核函式還可以通過函式組合得到，例如，

1. 若k1和k2是核函式，則對於任意整數r1、r2，其線性組合r1k1+r2k2也是核函式
2. 若k1和k2是核函式，則核函式的直積

也是核函式。

     3、若k1為核函式，則對於任意函式g(x)，

也是核函式。