一、 什麼是樹?

1，生活中的樹 ：

我們知道，對於一棵樹，無論大小， 都是由數根，樹幹，節點以及樹葉構成，那麼，在資料結構中，也存在樹這種結構，與之不同的是，它是一棵倒立的樹 ，模型如下所示：
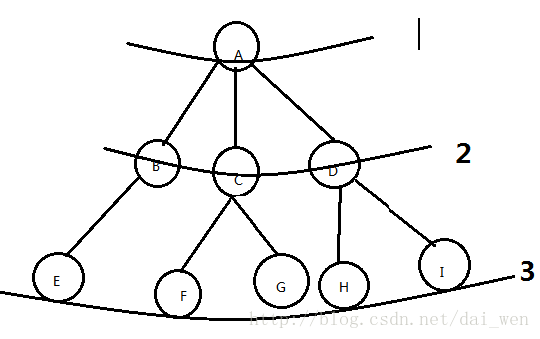
2，資料結構中的樹：

3，樹的基本概念：

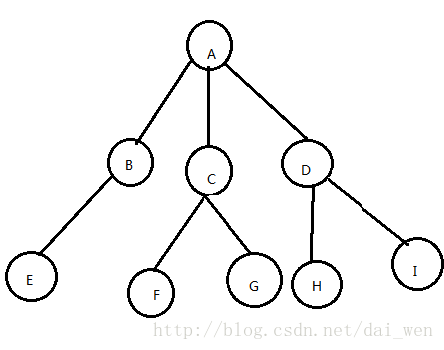
以上圖中的樹為例：

樹：由N(N>=0)個結點構成的集合，N=0時是一棵空樹 ，那麼對N>1的樹做出以下解釋：

1、根節點：故名思義，根節點相當於一棵樹的根，是樹的基礎，它是一個特殊的結點，根節點沒有前驅結點，是本樹所有結點的祖先。

如：A　就是該樹的根節點

2、除根節點外，其餘結點被分成M(M>0)個互不相交的集合T1、T2、……、Tm，其中：
（1）每一個集合Ti(1<= i <= m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，可以沒有後繼，也可以有多個後繼。

B，C，D是A的子樹，各自又是以自身為根節點的樹 ；

由此看出：樹是遞迴定義的。

3，結點：結點包括一個數據元素及若干指向其他子樹的分支(指標(索引))。
（Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇ，Ｈ，Ｉ）

４， 葉結點：度為0的結點稱為葉結點，葉節點也稱為終端節點。
（Ｅ，Ｆ，Ｇ，Ｈ，Ｉ）

５， 分支結點：度不為0的結點稱為分支結點，分支結點也稱為非終端節點，一棵樹中除葉節點外的所有節點都是分支結點。
（Ａ，Ｂ，Ｃ，Ｄ）

６， 祖先結點：從根節點到該結點所經分支上的所有節點。
（Ｅ的祖先結點是Ａ，Ｂ）
（Ｆ的祖先結點是Ａ，Ｃ）

７，子孫結點：以某節點為根節點的子樹中所有節點。
（Ａ的子孫結點為Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇ，Ｈ，Ｉ）

８，雙親結點：樹中某節點有孩子結點，則這個結點稱為它孩子結點的雙親結點，雙親結點也稱為前驅結點。
（Ｅ的雙親結點是Ｂ，Ｂ的雙親結點是Ａ）

９， 孩子結點：樹中一個節點的子樹的根節點稱為該結點的孩子結點，孩子結點也稱為後繼結點。
（Ａ的孩子節點是Ｂ，Ｃ，Ｄ）

１０，兄弟結點：具有相同雙親結點的結點稱為兄弟結點。
（Ａ為Ｂ，Ｃ，Ｄ的雙親結點，所以，Ｂ，Ｃ，Ｄ，互為兄弟結點）

１１， 結點的度：結點所擁有子樹的個數稱為該結點的度。
（Ａ的度為３）

１２， 樹的度：樹中所有節點的度的最大值稱為該樹的度。
（該樹中，所有結點度的最大值為３，故樹的度為３）

１３， 結點的層次：從根節點到樹中某節點所經路徑上的分支數稱為該結點的層次，根節點的層次為1， 其他結點層次是其雙親結點層次加1.

１４， 樹的深度：樹中所有節點的層次的最大值稱為該樹的深度。
（該樹的深度為３）

１５，有序樹：樹中結點的各棵子樹T0、T1…是有序的，即為有序樹。其中T1叫做根的第一棵子樹，T2叫根的第二棵子樹…

１６，無序樹：樹中結點的各棵子樹之間的次序不重要，可以相互交換位置。

１７，森林：樹m棵樹的集合(m大於等於0)。在自然界中樹和森林是兩個不同的概念，但在資料結構中，它們之間的差別很小。刪去一棵非空樹的根節點，樹就變成森林；反之若增加一個節點，讓森林中每一棵樹的根節點都變成他的子女，森林就變成一棵樹。

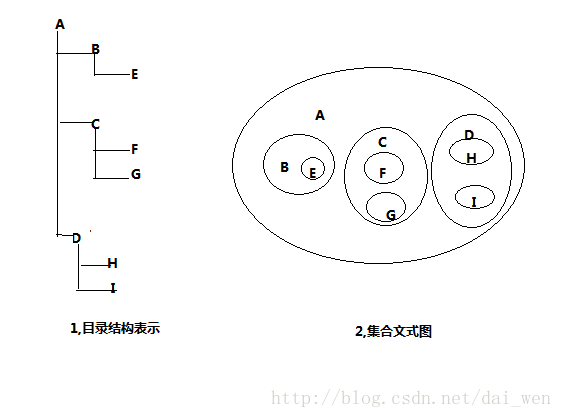
４，樹的表示方法：

（１）目錄結構表示：
（２）集合文示圖表示：　

　示意圖如下　：
　

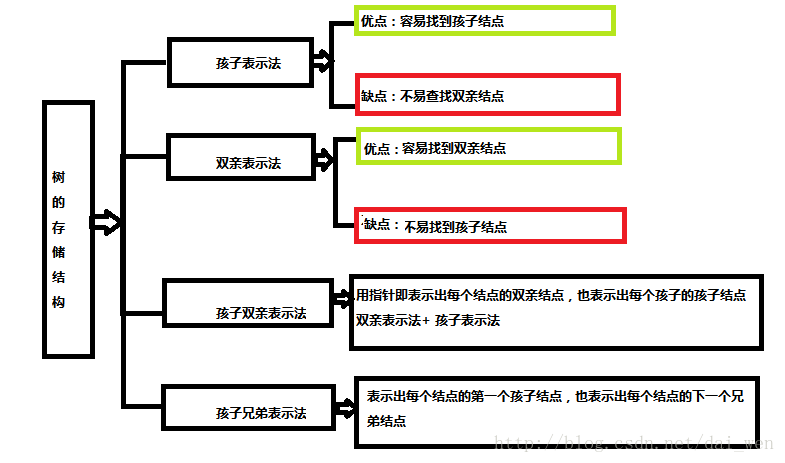
１，樹的儲存結構
計算機中儲存樹的資訊，要求既要儲存結點的資料元素資訊，又要儲存結點之間的邏輯關係資訊。

//最常用的是孩子表示法

二，什麼是二叉樹？　

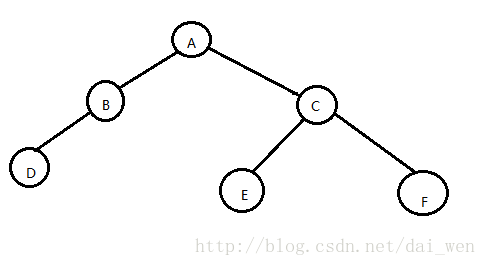
　　　　　　　　　　　　　　　　圖一
１，二叉樹：
一棵二叉樹是結點的一個有限集合，該集合或者為空，或者是由一個根節點加上兩棵分別稱為左子樹和右子樹的二叉樹組成。

２，二叉樹的五種形態：

３，二叉樹的特點：
（1）每個結點最多有兩棵子樹，即二叉樹不存在度大於2的結點

（2）二叉樹的子樹有左右子樹之分，其子樹的次序不能顛倒
　
４，滿二叉樹：
在一棵二叉樹中，如果所有分支結點都存在左子樹和右子樹，並且所有葉子節點都在同一層上。

５，完全二叉樹：
如果一棵具有N個結點的二叉樹的結構與滿二叉樹的前N個結點的結構相同，稱為完全二叉樹。

６，二叉樹的性質：　（以圖一為例）

1、若規定根節在點的層數為1，則一棵非空二叉樹的第i層上最多有 2^(i-1)個結點
其中(i>=1)
（如第三層，最多有２^（３－１）＝４個結點）

2、若規定只有根節點的二叉樹的深度為1，則深度為K的二叉樹的最大結點數是
2^k-1，其中(k>=0)
（２^4-1=15個結點）

3、對任何一棵二叉樹, 如果其葉結點個數為 n0, 度為2的非葉結點個數為 n2,則具有n個結點的完全二叉樹的深度k為log2(n+1)上取整。

（floor()……向下取整函式，ceil()……向上取整函式

４、對於具有n個結點的完全二叉樹，如果按照從上至下從左至右的順序對所有節點從0開始編號，則對於序號為i的結點有：

a：如果i>0，則序號為i結點的雙親結點的序號為(i-1)/2；如果i=0，則序號為i的結點為根節點，無雙親結點b：

ｂ：如果2i+1

//舉個例子：
//如果一棵完全二叉樹總共有１０００個節點，求它的度為２的結點，度為１的結點，以及葉子結點　共有多少個？　
//設度為０，為１，為２的結點分別有：Ｎ０，Ｎ１，Ｎ２個，則有：
//Ｎ０＋Ｎ１＋Ｎ２＝１０００；
//已知度為０的結點永遠比度為２的結點多一個，也就是Ｎ０＝Ｎ２＋１；
//則Ｎ１＋２Ｎ２＋１＝１０００；
//又因為總的結點個數為１０００，是偶數，所以，度為１的結點只有一個
//也就是說：１＋２Ｎ２＋１＝１０００?
//化簡得：Ｎ２＝９９８／２＝４９９；
//故而：Ｎ０＝Ｎ２＋１＝４９９＋１＝５００；
//Ｎ０＋Ｎ１＋Ｎ２＝５００＋１＋４９９＝１０００；與題意相符，說明計算正確；

７，二叉樹的儲存結構

二叉樹的儲存結構主要有三種：順序儲存、鏈式儲存和模擬指標(靜態連結串列)儲存結構。

（１）樹的遍歷：

//前序遍歷(根結點＋左子樹＋右子樹)
//中序遍歷（左子樹＋根結點＋右子樹）
//後序遍歷（左子樹＋右子樹＋根結點）
//前，中，後指的是遍歷根結點的次序

（２）【順序儲存】

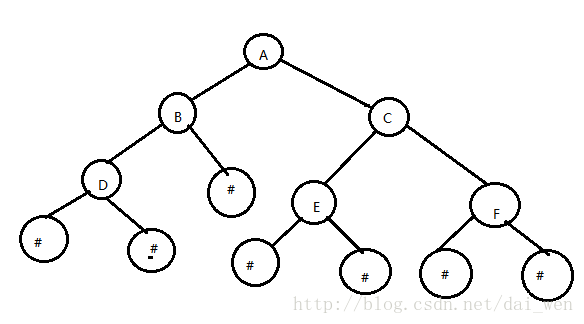
設有一棵二叉樹(最好完全二叉樹)，對它所有的結點按照層次次序自頂向下，同一層自左向右順序編號，就得到一個節點的順序序列。對於一般的二叉樹，為了能找到某一結點的上下左右關係，也必須仿照完全二叉樹的方式來儲存，遇到空樹，在順序表中應該將該位置空出來。
（如下將空樹用＃表示）

三,樹的基本操作:

1.二叉樹的實現：

#include<stdio.h>
#include<queue>
#include<stack>
#include<list>
#include<iostream>
using namespace std;

//二叉樹節點
template<class T>
struct BinaryTreeNode
{
    BinaryTreeNode()
        :_pLeft(NULL)
        ,_pRight(NULL)
    {}
    T _data;//資料
    BinaryTreeNode<T>* _pLeft;//左孩子
    BinaryTreeNode<T>* _pRight;//右孩子
};

//二叉樹
template<class T>
class BinaryTree
{
public:
typedef BinaryTreeNode<T> Node;
private:
Node* _pRoot;//根節點
}

2.二叉樹的基本操作：

1).二叉樹的建立：

BinaryTree()//空二叉樹的建構函式
        :_pRoot(NULL)
    {}
    //帶引數二叉樹的建構函式，arr為前序遍歷得到的一組序列
    BinaryTree(const T arr[],size_t size,T& invalid)
    {
        size_t index = 0;
    }

//封裝的底層函式       
_CreateBinaryTree(_pRoot,arr,size,index,invalid);//建立二叉樹  
{
  void _CreateBinaryTree(Node*& pRoot,const T arr[],size_t size,size_t& index,T& invalid)//建立二叉樹
    {
     if(arr==NULL || size<=0 || index<0 || index>size+2)//判斷引數合法性
     return;
 if(arr[index]!=invalid)
   {
      pRoot = new Node;
      pRoot->_data = arr[index];
 _CreateBinaryTree(pRoot->_pLeft,arr,size,++index,invalid);
 //注意index是不斷加一的，不能用index+1或者index++來替換++index,因為在回退的過程中index也會回退
 _CreateBinaryTree(pRoot->_pRight,arr,size,++index,invalid);//同時也要注意index做引數要用引用接收，也是為了避免這個問題
   }
  }
 }

2).二叉樹的拷貝建構函式

BinaryTree(const BinaryTree<T> & t)//二叉樹的拷貝建構函式
    {
        _pRoot = _CopyBinaryTree(t._pRoot);
    }

Node* _CopyBinaryTree(Node* pRoot)//拷貝二叉樹
    {
        Node* pCur = NULL;
        if(pRoot != NULL)
        {
            pCur = new Node;
            pCur->_data = pRoot->_data;
            pCur->_pLeft = _CopyBinaryTree(pRoot->_pLeft);
            pCur->_pRight = _CopyBinaryTree(pRoot->_pRight);
        }
        return pCur;
    }

3).二叉樹的賦值運算子過載

 BinaryTree<T>& operator=(const BinaryTree<T>& t)//二叉樹的賦值運算子過載
    {
        if(this != &t)
        {
            _DestoryBinaryTree(_pRoot);//先析構*this
            _pRoot = _CopyBinaryTree(t._pRoot);//再用t拷貝構造*this
        }
        return *this;
    }

4).二叉樹的解構函式

~BinaryTree()//析構二叉樹
    {
        _DestoryBinaryTree(_pRoot);
    }

void _DestoryBinaryTree(Node* &pRoot)//銷燬二叉樹(利用後序遍歷，先刪除左節點，再刪除右節點，最後刪除根節點)
    {
        if(pRoot != NULL)
        {
            _DestoryBinaryTree(pRoot->_pLeft);
            _DestoryBinaryTree(pRoot->_pRight);
            delete pRoot;
            pRoot = NULL;
        }
    }