樹及二叉樹筆記

阿新 • • 發佈：2019-05-16

poll() .net 溢出 println 完成 png 數據結構類型 index 操作

數據結構之樹（Tree）

筆者本來是準備看JDK HashMap源碼的，結果深陷紅黑樹中不能自拔，特撰此篇以加深對樹的理解

定義

首先來看樹的定義：

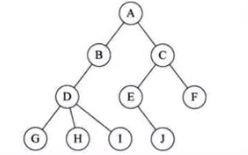
樹（Tree）是n（n≥0）個節點的有限集。n = 0 時稱為空樹。在任意一棵非空樹中：1、有且僅有一個特定的節點稱為根（Root）的節點。2、當n > 1時，其余節點可分為m（m > 0）個互不相交的有限集T1、T2、T3、……Tm，其中每一個集合本身又是一棵樹，並稱為根的子樹（SubTree）。

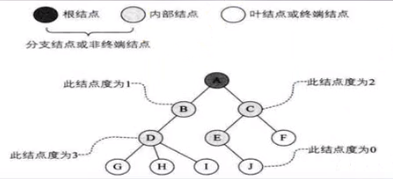
節點的度：節點擁有子樹數稱為節點的度。（也就是該節點擁有的子節點數）度為0的節點稱為非終端節點或分支節點，除根節點外，分支節點也稱為內部節點，樹的度是樹內各節點度的最大值。

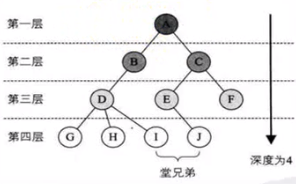
節點的層次與深度：節點的層次（Level）從根開始定義，根為第一層，根的孩子為第二層。若A節點在第l層，則其子樹的根就在第l+1層（即A節點的子節點）。其雙親在同一層的節點互為堂兄弟。樹中節點的最大層次稱為樹的深度（Depth）或高度。

樹的存儲結構

簡單的順序存儲不能滿足樹的實現，需要結合順序存儲和鏈式存儲實現。
三種表示方法：

雙親表示法
孩子表示法
孩子兄弟表示法
孩子雙親表示法

雙親表示法：

在每個節點中，附設一個指示器，指示其雙親節點在鏈表中的位置。
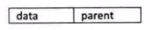
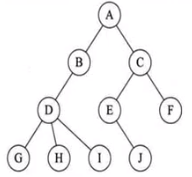
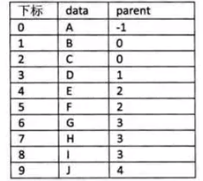
技術分享圖片

缺點：找父節點容易，找子節點難。

孩子表示法：

方案一：
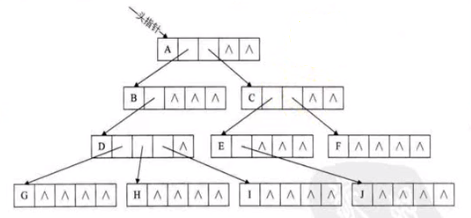
技術分享圖片
缺點：大量空指針造成浪費
方案二：

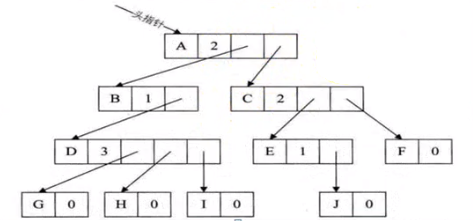
缺點：維護困難，不易實現。

也未解決找父節點容易，找子節點難的問題。

孩子兄弟表示法

任意一棵樹，他的結點的第一個孩子如果存在就是唯一結點，他的右兄弟如果存在，也是唯一的，因此，我們設置兩個指針，分別指向該結點的第一個孩子和該結點的右兄弟（I不是G的右兄弟）
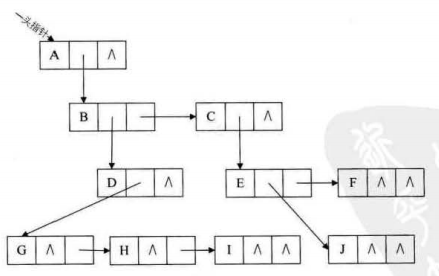
技術分享圖片

孩子雙親表示法

用順序存儲和鏈式存儲組合成散列鏈表，可以通過獲取頭指針獲取該元素父節點。
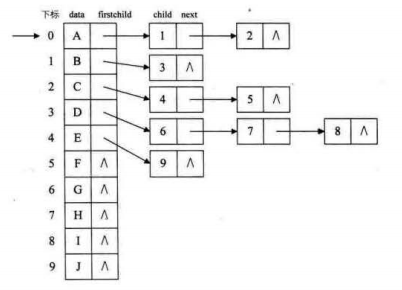
技術分享圖片
不太清楚？那就將元素的父節點單獨列出來：

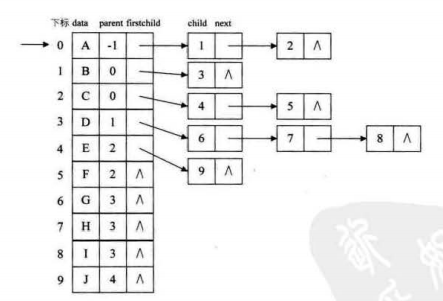
二叉樹

二叉樹是每個結點最多有兩個子樹的樹結構

斜樹

所有節點都只有左子樹的二叉樹叫做左斜樹。所有節點都只有右子樹的二叉樹叫做右斜樹。兩者統稱為斜樹。

技術分享圖片
線性表結構可以理解為樹的一種表達形式。

滿二叉樹

所有分支節點都存在左子樹和右子樹，並且所有葉子都在同一層上，這樣的二叉樹稱為滿二叉樹。

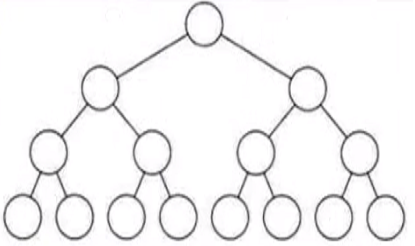
技術分享圖片

完全二叉樹

對於一個有n個節點的二叉樹按層序編號，如果編號為i（1 ≤ i ≤ n）的節點與同樣深度的滿二叉樹中編號為i的節點在二叉樹中位置完全相同則該二叉樹稱為完全二叉樹。
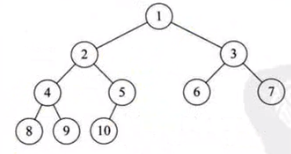
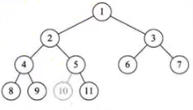
技術分享圖片

二叉樹的性質：

性質1：二叉樹第i層上的結點數目最多為 2^i-1 ( i ≥1 )。
性質2：深度為k的二叉樹至多有2^k-1個結點( k ≥ 1 )。
性質3：包含n個結點的二叉樹的深度至少為log₂ (n+1)。
性質4：在任意一棵二叉樹中，若終端結點的個數為n₀，度為2的結點數為n₂，則n₀=n₂+1。
性質5：對於一個有n個節點的完全二叉樹（深度為log₂ (n+1)），節點按層序編號（從第一層到log₂ (n+1)，每層從左到右），對任意一個節點i有：對於第i個非根節點，其父節點是第i/2個。

Java實現二叉樹及其遍歷

這裏我們采用的結構是二叉鏈表：
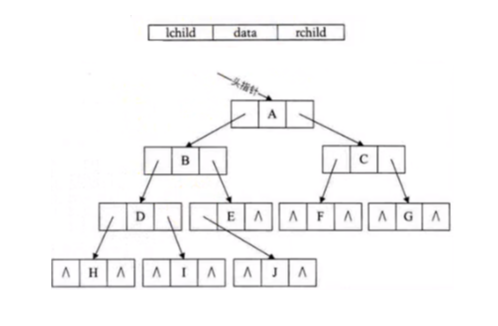
技術分享圖片

新建一個BinaryTree的類，並初始化一個測試樹：

class BinaryTree

public class BinaryTree {
    private Node root=null;

    public void createTestBinaryTree(){
        /**
         *            A
         *           /           *          B    C
         *        /  \              *       D    E     F
         *
         */
        root=new Node(1,"A");
        Node nodeB=new Node(2,"B");
        Node nodeC=new Node(3,"C");
        Node nodeD=new Node(4,"D");
        Node nodeE=new Node(5,"E");
        Node nodeF=new Node(6,"F");
        root.leftChild=nodeB;
        root.rightChild=nodeC;
        nodeB.leftChild=nodeD;
        nodeB.rightChild=nodeE;
        nodeC.rightChild=nodeF;
        //這麽寫太蠢了。以後再更新二叉樹的構建。。。
    }

    //由數組構造二叉樹。
    public void createTestBinaryTree2(){
    /**
        *            A
        *           /          *          B    C
        *        /  \   /
        *       D    E F
        *
        */

    String[] strings=new String[]{"A","B","C","D","E","F"};
    List<Node> nodes=new ArrayList<>();
    for (int i = 0; i < strings.length; i++) {
        Node node = new Node(i,strings[i]);
        nodes.add(node);
    }
    root=nodes.get(0);
    //如果root為第一個節點，則第i個節點的左子節點是第2i個
    //這裏i是從0開始的
    for (int i = 0; i < nodes.size(); i++) {
        if ((2*i+1)<nodes.size()){
            nodes.get(i).leftChild=nodes.get(2*i+1);
        }
        if ((2*i+2)<nodes.size()){
            nodes.get(i).rightChild=nodes.get(2*i+2);
        }
    }
}

根據該結構構造其節點類與get方法：

class Node

public class Node<T>{
    private int index;
    private T data;
    private Node leftChild;
    private Node rightChild;

    public Node(int index,T data){
        this.index=index;
        this.data=data;
        this.leftChild=null;
        this.rightChild=null;
    }

    public int getIndex() {
        return index;
    }

    public T getData() {
        return data;
    }
}

然後是樹深度和節點數的方法：

height方法和size方法

public int height(){
    return getHeight(root);
}

private int getHeight(Node node){
    if (node ==null){
        return 0;
    }else {
        int i=getHeight(node.leftChild);
        int j=getHeight(node.rightChild);
        return i>j?i+1:j+1;//遍歷1層就增加了1，i和j哪個大返回哪個
    }
}
public int size(){
    return getsize(root);
}

private int getsize(Node node){
    if (node==null){
        return 0;
    }else {
        return 1+getsize(node.leftChild)+getsize(node.rightChild);//遍歷一個節點增加1，最後總數就是節點數
    }
}

接著就是四種遍歷方法：先序遍歷、中序遍歷、後序遍歷，層序遍歷。先序、中序、後序是指root節點出現的方式。比如一個只有三個節點的二叉樹，先序就是先遍歷讀取根節點，再左再右；中序就是先左，後根，然後右，後序先左後右，最後根。層序就是從上到下、從左到右依次讀取。
比較簡單容易理解的方式是遞歸：

先序遍歷（遞歸）

public void preOrder(){
    preOrder(root);
    return;
}

private void preOrder(Node node){
    if (node==null){
        return;
    }else{
        System.out.println("先序遍歷："+node.data);
    }
    if (node.leftChild!=null){
        preOrder(node.leftChild);
    }
    if (node.rightChild!=null){
        preOrder(node.rightChild);
    }
}

中序遍歷（遞歸）

```java public void midOrder(){ midOrder(root); return; } private void midOrder(Node node){ if (node.leftChild!=null){ midOrder(node.leftChild); } if (node==null){ return; }else{ System.out.println("中序遍歷："+node.data); } if (node.rightChild!=null){ midOrder(node.rightChild); } } ```

後序遍歷（遞歸）

```java public void postOrder(){ postOrder(root); return; } private void postOrder(Node node) { if (node.leftChild != null) { postOrder(node.leftChild); } if (node.rightChild != null) { postOrder(node.rightChild); } if (node==null){ return; }else{ System.out.println("後序遍歷："+node.data); } } ```

三種遍歷都能用遞歸的方式，但是遞歸運行效率較低，並且樹大了之後很容易溢出，可以用棧和循環代替遞歸：

先序遍歷（棧）

```java public void nonRecPreOrder(){ nonRecPreOrder(root); return; } private void nonRecPreOrder(Node node){ if (node==null){ return; } Stack stack=new Stack<>(); stack.push(node); while (!stack.isEmpty()){ Node theNode=stack.pop(); if (theNode.rightChild!=null){ stack.push(theNode.rightChild); } if (theNode.leftChild!=null){ stack.push(theNode.leftChild); } System.out.println("先序遍歷（棧）："+theNode.data); } } ```

先序遍歷2（棧）

```java public void nonRecPreOrder2() { nonRecPreOrder2(root); return; } private void nonRecPreOrder2(Node node) { //非遞歸實現 Stack stack = new Stack<>(); while (node != null || !stack.isEmpty()) { while (node != null) { System.out.println("先序遍歷2（棧）:" + node.data); stack.push(node); node = node.leftChild; } if (!stack.isEmpty()) { node = stack.pop(); node = node.rightChild; } } } ```

中序遍歷（棧）

```java public void nonRecMidOrder(){ nonRecMidOrder(root); return; } private void nonRecMidOrder(Node node){ if (node==null){ return; } Stack stack=new Stack<>(); Node p = root;//輔助節點 stack.add(p); while(!stack.isEmpty()) { //只要你有左孩子，就將左孩子壓入棧中 if(p!=null && p.leftChild!=null) { stack.add(p.leftChild); p=p.leftChild; }else { p = stack.pop();//彈出棧頂節點左孩子--->根節點 System.out.println("中序遍歷（棧）"+p.data);//訪問 if(p!=null && p.rightChild!=null) {//如果棧點元素有右孩子的話，將有節點壓入棧中 stack.push(p.rightChild); p = p.rightChild; }else p = null;//p=stk.pop;已經訪問過p了，p設置為null } } } ```

先序遍歷2（棧）

```java public void nonRecMidOrder2() { nonRecMidOrder2(root); return; } private void nonRecMidOrder2(Node node) { //中序遍歷費遞歸實現 Stack stack = new Stack<>(); while (node != null || !stack.isEmpty()) { while (node != null) { stack.push(node); node = node.leftChild; } if (!stack.isEmpty()) { node = stack.pop(); System.out.println(node.data); node = node.rightChild; } } } ```

後序遍歷（棧）

```java public void nonRecPostOrder() { nonRecPostOrder(root); return; } private static void nonRecPostOrder(Node biTree) { //後序遍歷非遞歸實現 int left = 1;//在輔助棧裏表示左節點 int right = 2;//在輔助棧裏表示右節點 Stack stack = new Stack<>(); Stack stack2 = new Stack<>();//輔助棧，用來判斷子節點返回父節點時處於左節點還是右節點。 while (biTree != null || !stack.empty()) { while (biTree != null) {//將節點壓入棧1，並在棧2將節點標記為左節點 stack.push(biTree); stack2.push(left); biTree = biTree.leftChild; } while (!stack.empty() && stack2.peek() == right) {//如果是從右子節點返回父節點，則任務完成，將兩個棧的棧頂彈出 stack2.pop(); System.out.println(stack.pop().data); } if (!stack.empty() && stack2.peek() == left) {//如果是從左子節點返回父節點，則將標記改為右子節點 stack2.pop(); stack2.push(right); biTree = stack.peek().rightChild; } } } ```

層次遍歷（隊列）

```java public void levelOder(){ levelOrder(root); return; } private void levelOrder(Node node){ //層次遍歷 /* 1.對於不為空的結點，先把該結點加入到隊列中 2.從隊中拿出結點，如果該結點的左右結點不為空，就分別把左右結點加入到隊列中 3.重復以上操作直到隊列為空 */ if(node == null) return; LinkedList list = new LinkedList(); list.add(node); Node currentNode; while(!list.isEmpty()) { currentNode = list.poll(); System.out.println("層序遍歷（隊列）"+currentNode.data); if(currentNode.leftChild != null) list.add(currentNode.leftChild); if(currentNode.rightChild != null) list.add(currentNode.rightChild); } } ```

這裏，後序遍歷和層次遍歷參考了這個博客，特別是後序遍歷，筆者對於遞歸函數非遞歸化還有待提高，遞歸函數雖然簡單易懂，但是數據量大了之後特別容易爆棧，所有的遞歸函數都可以非遞歸化，因此優先考慮非遞歸函數。
樹是一種重要的數據結構類型，通過對二叉樹的研究，筆者對棧的用法有了更深的理解。

樹及二叉樹筆記

poll() .net 溢出 println 完成 png 數據結構類型 index 操作數據結構之樹（Tree）筆者本來是準備看JDK HashMap源碼的，結果深陷紅黑樹中不能自拔，特撰此篇以加深對樹的理解定義首先來看樹的定義：樹（Tree）是n（n≥0）個

樹及二叉樹筆記

數據結構之樹（Tree）

定義

樹的存儲結構

雙親表示法：

孩子表示法：

孩子兄弟表示法

孩子雙親表示法

二叉樹

斜樹

滿二叉樹

完全二叉樹

二叉樹的性質：

Java實現二叉樹及其遍歷

樹及二叉樹筆記

前序中序，中序後序建立二叉樹及二叉樹的深度

圖解二叉樹及二叉樹遍歷

二叉樹及二叉樹的應用

樹及二叉樹（資料結構）

資料結構之二叉排序樹及二叉樹的遍歷

【樹】二叉樹遍歷算法（深度優先、廣度優先遍歷，前序、中序、後序、層次）及Java實現

資料結構筆記：樹到二叉樹的轉換

資料結構與演算法學習--二叉樹及二叉搜尋樹

c++樹及樹與二叉樹的轉換

資料結構(Java筆記)—樹（二叉樹）

L2-011玩轉二叉樹（二叉樹重建及層序遍歷）

排序方法及二叉樹

瘋狂java筆記之樹和二叉樹

樹與二叉樹5之B樹、B+樹及R樹

java資料結構與演算法之樹基本概念及二叉樹（BinaryTree）的設計與實現

二叉樹及的性質及二叉樹的Python實現

資料結構筆記整理第5章：樹和二叉樹

利用棧結構實現二叉樹的非遞迴遍歷，求二叉樹深度、葉子節點數、兩個結點的最近公共祖先及二叉樹結點的最大距離

用Python實現二叉樹、二叉樹非遞迴遍歷及繪製

樹及二叉樹筆記

數據結構之樹（Tree）

定義

樹的存儲結構

雙親表示法：

孩子表示法：

孩子兄弟表示法

孩子雙親表示法

二叉樹

斜樹

滿二叉樹

完全二叉樹

二叉樹的性質：

Java實現二叉樹及其遍歷

相關推薦