支援向量機（Support Vector Machine，SVM)，可以完成對資料的分類，包括線性可分情況和線性不可分情況。
1、線性可分
首先，對於SVM來說，它用於二分類問題，也就是通過尋找一個分類線(二維是直線，三維是平面，多維是超平面）可以將資料分為兩類。 並用線性函式f(x)=w·x +b來構造這個分類器(如下圖是一個二維分類線）

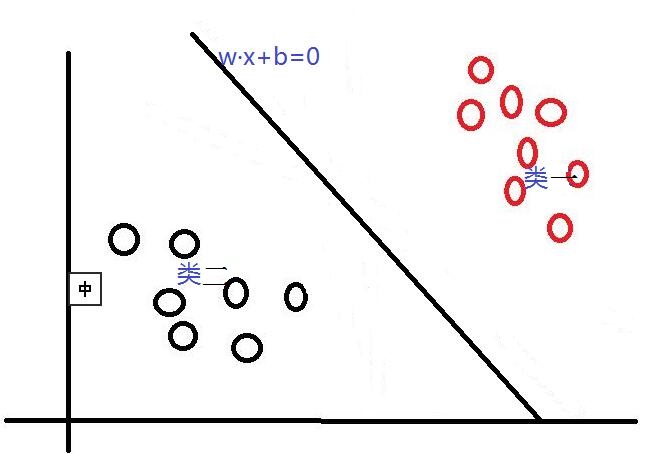
其中，w是權重向量，x為訓練元組（X=(x1,x2…xn),n為特徵個數，xi為每個X在屬性i上對應的值），b為偏置，w·x是w和x的點積。當某資料被分類時，就會代入此函式，通過計算f(x)的值來確定所屬的類別，當f(x)>0時，此資料被分為類一，當f(x)<0時，此資料被分為類二。通過觀察，我們可以發現，如果我們平移或者旋轉一下此分類線，同樣可以完成資料的分類（如下圖），那麼，選擇哪一個分類線才是最好的呢？

對於這個問題，SVM是通過搜尋“最大邊緣距離分類線”（面）來解決的。那麼，什麼是邊緣距離，為什麼要尋找最大的邊緣距離呢？如下圖所示，如果我們將某一分類線向右平移，在平移到右側最大限度，又能確保此時的這個被平移的線仍然能將資料分為兩類時，也就是如下圖（線一）所示的：右側與類一中某個或某些資料（實心點）相交的位置。此時正好，線上右側和線上的資料是類一，線上左側的資料是類二；同理，如果我們將這個分類線向左移動，也是移動到左側最大限度（如下圖線二），此時這條線剛好也與類二中的某個或某些（實心點）資料相交，線上和線左側的資料是類二，線右側的資料是類一。對於這兩條“極限邊界線”，我們可以稱之為支援線，或者對於面來說，就是支援面，而確定這些支援面或者支援線的那些資料點，我們稱之為支援向量。兩個支援線或支援面之間的這個距離，就是我們所說的邊緣距離。

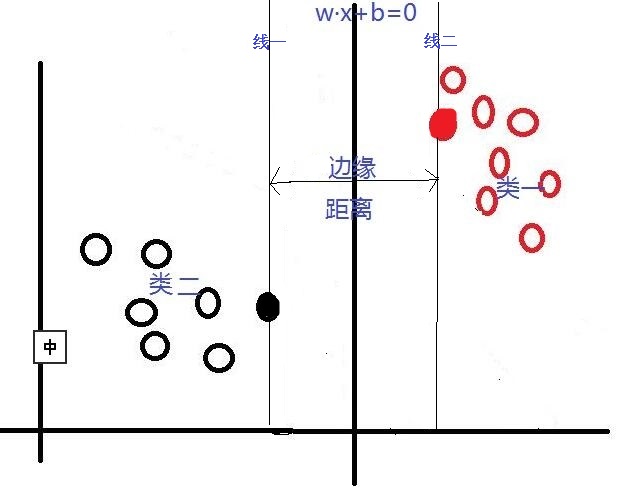
在這裡我們可以發現，不同的分類線（面）會對應不同的支援線(面），支援線（面）之間的邊緣距離也是不同的，並且，我們認為：邊緣距離越大的分類線，對分類精度更有保證，所以，我們要找的”最好的“分類線（面），就是擁有最大邊緣距離的那個分類線（面）。也就是說：對於線性可分的情況，SVM會選擇最大化兩類之間邊緣距離的那個分類線（面）來完成二分類問題。並且此分類線（面）平行於兩個支援線（面），平分邊緣距離。下圖是一個與上圖相比，擁有更大邊緣距離的分類線（面）。

2、線性不可分
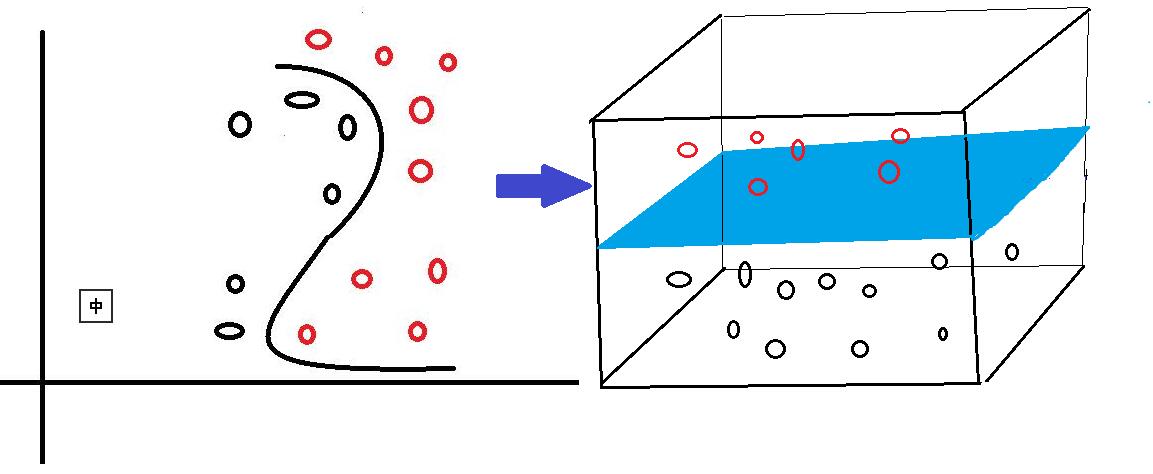
對於線性可分的情況，我們上面說到，可以通過一個線性函式f(x)=w·x +b來構造一個分類器，尋找一個有著最大邊緣距離的分類線（面）來完成對資料的分類。但是，我們還會遇到另一個問題，就是，如果資料是線性不可分的情況，用一個二維直線，三維平面或者多維超平面不能完成二分類，又該如何呢？對於線性不可分問題，SVM採取的方法是將這些線性不可分的原資料向高維空間轉化，使其變得線性可分。就像下圖所示，對於一些資料，他們是線性不可分的，那麼，通過將他們向高維轉化，也許就像圖中所示，將二維資料轉化到三維，就可以通過一個分類面將這些資料分為兩類。所以說，SVM通過將線性不可分的資料對映到高維，使其能夠線性可分，再應用線性可分情況的方法完成分類。

而在這個高維轉化過程中，SVM實際上並沒有真正的進行高維對映，而是通過一種技巧來找出這個最大邊緣分類面，即將一個叫做核函式的函式，應用於原輸入資料上。這個技巧首先允許我們不需要知道對映函式是什麼，只將選定的核函式應用到原輸入資料上就行；其次，所有的計算都在原來的低維輸入資料空間進行，避免了高維運算。對於這個核函式，可選項有好幾種，包括多項式核函式，高斯徑向基函式核函式，S型核函式等等。
下面寫了兩個matlab程式，來簡單的看了一下matlab自帶的SVM分類器的分類效果。在這裡主要應用兩個函式來完成而分類問題：
（1)svmtrain函式，其是一個訓練分類模型的函式：SVMStruct = svmtrain(Training,Group,Name,Value），其輸入引數為（訓練資料，訓練資料相應組屬性，可選引數名，可選引數的值），輸出為一個結構體。
可選引數有很多，包括boxconstraint，kernel_function，kernelcachelimit，kktviolationlevel，method，kktviolationlevel，mlp_params，options，polyorder，rbf_sigma，showplot，tolkkt，這裡我介紹一下我下面例子中要用到的兩個可選輸入引數：
1、kernel_function（核函式型別）：可選的核函式有linear，quadratic，polynomial，rbf，mlp，@kfun ，如果不設定核函式型別，那麼預設的選用線性核函式linear。
2、showplot(繪圖）：是一個布林值，用來指示是否繪製分類資料（這裡是訓練資料）和分類線。但是這個繪圖功能只支援繪製有兩個特徵值的資料，也就是二維的點資料。（預設為false)，在svmtrain函式中，如果將showplot設定為true，程式會自動在figure中用不同的顏色繪製出訓練資料中兩個類的點以及通過訓練資料獲得的分類線，並標註出哪些點是支援向量。（如下圖是一組訓練資料在通過svmtrain函式訓練後，應用showplot繪製出的圖形，其中，紅色的+代表訓練集類1中的資料，綠色的星號代表訓練集類2中的資料。支援向量被O圈起。）

3、boxconstraint
svmtrain函式輸出的結構體中包含訓練出的分類器的資訊，包括支援向量機，偏置b的值等等。
（2）svmclassify函式，其實一個應用訓練的分類模型和測試資料進行分類測試的函式：Group = svmclassify(SVMStruct,Sample,’Showplot’,true)，其最多隻有這四個輸入引數，包括（訓練出的分類模型結構體，測試資料，繪圖顯示，’true’）。在svmclassify函式中用Showplot繪圖，會繪製出svmclassify函式中輸入的測試資料點，如下圖所示，粉色的+為被分到類1中的測試資料，藍色星號是被分到類2中的測試資料）

對於svmclassify函式的輸出Group，其是一個n*1的陣列，裡面的n為測試資料個數，陣列中每個元素記錄的是對應順序下的測試資料被分類後的類屬性。
測試1程式碼：

    function [ classification ] = SVM_L( train,test )
%  進行SVM線性可分的二分類處理
%  1、首先需要一組訓練資料train，並且已知訓練資料的類別屬性，在這裡，屬性只有兩類，並用1，2來表示。
%  2、通過svmtrain（只能處理2分類問題）函式，來進行分類器的訓練
%  3、通過svmclassify函式，根據訓練後獲得的模型svm_struct，來對測試資料test進行分類
train=[0 0;2 4;3 3;3 4;4 2;4 4;4 3;5 3;6 2;7 1;2 9;3 8;4 6;4 7;5 6;5 8;6 6;7 4;8 4;10 10];                                              %訓練資料點
group=[1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2]'; %訓練資料已知分類情況
                                                                            %與train順序對應
test=[3 2;4 8;6 5;7 6;2 5;5 2];                                                    %測試資料

%訓練分類模型
svmModel = svmtrain(train,group,'kernel_function','linear','showplot',true);

%分類測試
classification=svmclassify(svmModel,test,'Showplot',true);
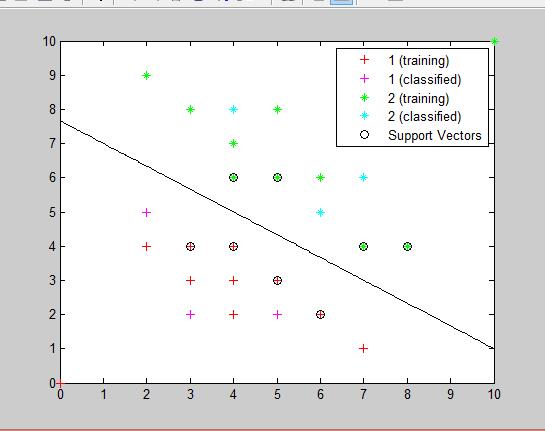
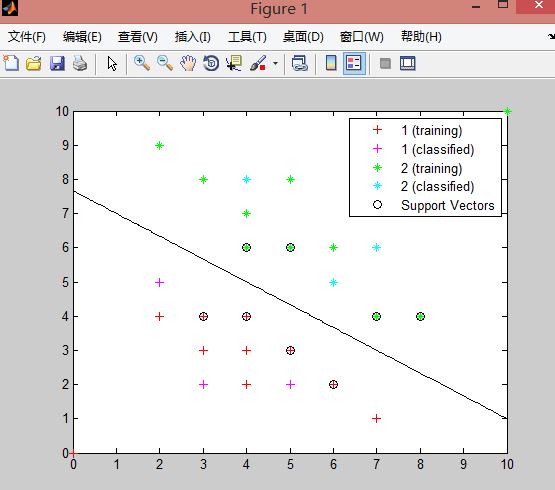
end

線性可分實驗結果如下圖，輸出的測試資料分類情況為（1 2 2 2 1 1），全部正確

測試2程式碼：

function [ classfication ] = SVM_NL( train,tast )
%SVM對線性不可分的資料進行處理
%在選擇核函式時，嘗試用linear以外的rbf,quadratic,polynomial等，觀察獲得的分類情況
%訓練資料
train=[5 5;6 4;5 6;5 4;4 5;8 5;8 8;4 5;5 7;7 8;1 2;1 4;4 2;5 1.5;7 3;10 4;4 9;2 8;8 9;8 10]; 
%訓練資料分類情況                                                                                      
group=[1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2];                          
%測試資料
test=[6 6;5.5 5.5;7 6;12 14;7 11;2 2;9 9;8 2;2 6;5 10;4 7;7 4];                 

%訓練分類模型
svmModel = svmtrain(train,group,'kernel_function','rbf','showplot',true);
%分類
classification=svmclassify(svmModel,test,'Showplot',true);
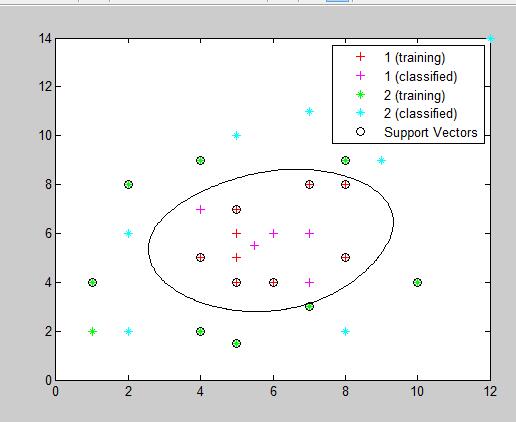
end

線性不可分（使用rbf核函式）的實驗結果如下圖，輸出的測試資料分類情況為（1 1 1 2 2 2 2 2 2 1 1），全部正確

因為實驗資料是二維的（有兩個特徵值），可以通過Showplot顯示出資料點的分類情況以及最大邊界分類線，，且實驗資料間干擾較小，分類效果很好。下面的實驗將選用matlab提供的一組分類資料來測試一下特徵數量對實驗精度的影響

測試3程式碼：

function [ classfication ] = SVM2_2( train,test )
%使用matlab自帶的關於花的資料進行二分類實驗（150*4），其中，每一行代表一朵花，
%共有150行（朵)，每一朵包含4個屬性值（特徵），即4列。且每1-50，51-100，101-150行的資料為同一類，分別為setosa青風藤類，versicolor雲芝類，virginica錦葵類
%實驗中為了使用svmtrain（只處理二分類問題）因此，將資料分為兩類，51-100為一類，1-50和101-150共為一類
%實驗先選用2個特徵值，再選用全部四個特徵值來進行訓練模型，最後比較特徵數不同的情況下分類精度的情況。

load fisheriris                       %下載資料包含：meas（150*4花特徵資料）
                                      %和species（150*1 花的類屬性資料）
meas=meas(:,1:2);                   %選取出資料前100行，前2列
train=[(meas(51:90,:));(meas(101:140,:))]; %選取資料中每類對應的前40個作為訓練資料
test=[(meas(91:100,:));(meas(141:150,:))];%選取資料中每類對應的後10個作為測試資料
group=[(species(51:90));(species(101:140))];%選取類別標識前40個數據作為訓練資料

%使用訓練資料，進行SVM模型訓練
svmModel = svmtrain(train,group,'kernel_function','rbf','showplot',true);
%使用測試資料，測試分類效果
classfication = svmclassify(svmModel,test,'showplot',true);

%正確的分類情況為groupTest，實驗測試獲得的分類情況為classfication
groupTest=[(species(91:100));(species(141:150))]; 
%計算分類精度
count=0;
for i=(1:20)
   if strcmp(classfication(i),groupTest(i))
      count=count+1;
   end
end
fprintf('分類精度為：%f\n' ,count/20);

end

選取資料中前兩個特徵值，進行實驗獲得的實驗精度為0.80，如下圖：

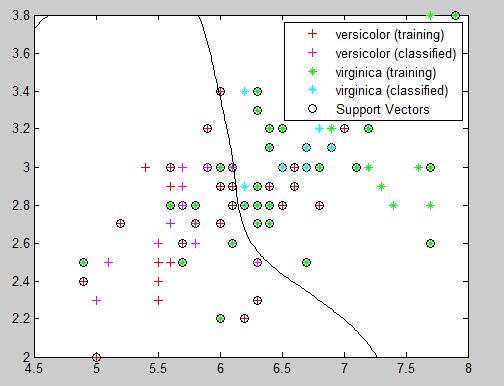
將上面實驗3中的程式碼”meas=meas(:,1:2); “改為“meas=meas(:,1:4);” 也就是選取了全部四個特徵值，此時的分類結果不能再用showplot打印出，但是，獲得的分類精度為1.0 ，這說明，選擇適當的特徵數量，對分類模型的準確度是有很大影響的。