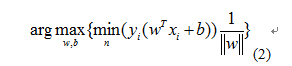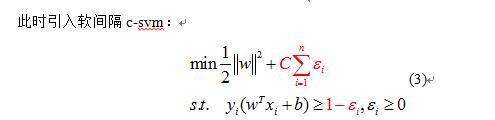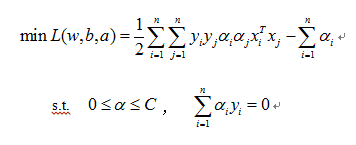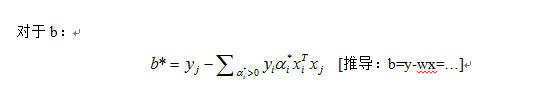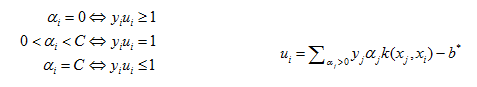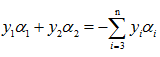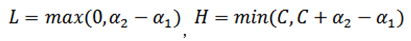本次內容主要講解什麼是支援向量，SVM分類是如何推導的，最小序列SMO演算法部分推導。

最後給出線性和非線性2分類問題的smo演算法matlab實現程式碼。

一、什麼是支援向量機(Support Vector Machine)

本節內容部分翻譯Opencv教程：

SVM是一個由分類超平面定義的判別分類器。也就是說給定一組帶標籤的訓練樣本，演算法將會輸出一個最優超平面對新樣本(測試樣本)進行分類。

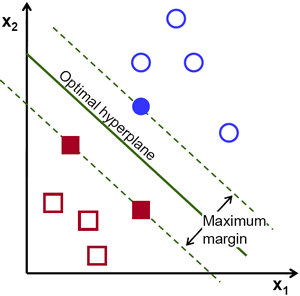
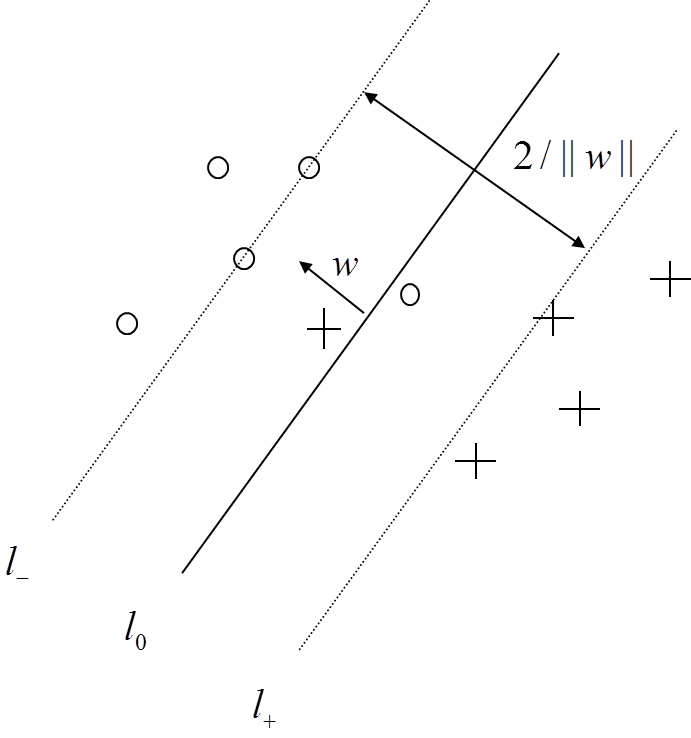
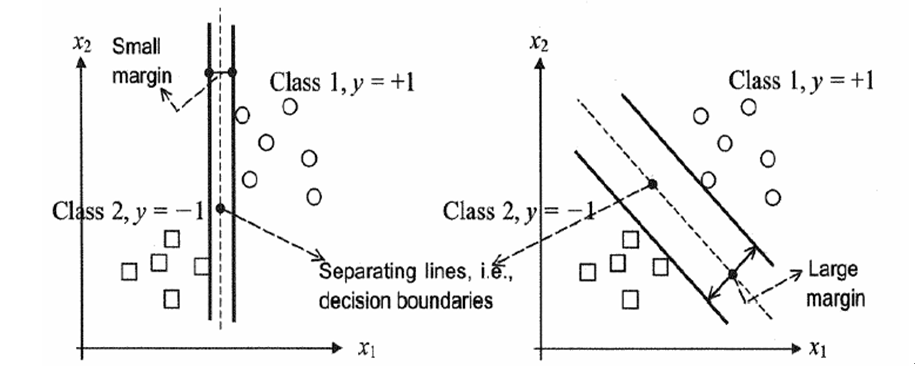
什麼樣的超平面才是最優的？我們考慮如下場景：對於一個由二維座標點構成的線性可分集合，如何找到一條直線將兩類座標分隔開？

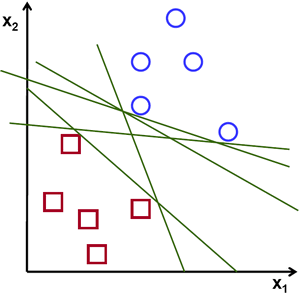
      上圖中，你可以看到存在多條直線將兩類座標分開。它們中有沒有最好的？我們可以直觀地定義如下規則：如果一條分割的直線離座標點太近，那它就不是最佳的。因為它會對噪聲敏感，不能正確的推廣。因此，我們的目標是找到一條分割線，它要離所有的樣本點都儘可能的遠。

       SVM演算法就是找一個超平面，並且它到離他最近的訓練樣本的距離要最大。即最優分割超平面最大化訓練樣本邊界。

原諒哥的翻譯水平，看著自己也彆扭，重新整理下：

對線性可分集，總能找到使樣本正確劃分的分介面，而且有無窮多個，哪個是最優？ 必須尋找一種最優的分界準則，是兩類模式分開的間隔最大。

在介紹如何推到之前，瞭解一個定義：

分隔超平面：上述將資料集分割開來的直線叫做分隔超平面。

超平面：如果資料集是N維的，那麼就需要N-1維的某物件來對資料進行分割。該物件叫做超平面，也就是分類的決策邊界。

間隔：

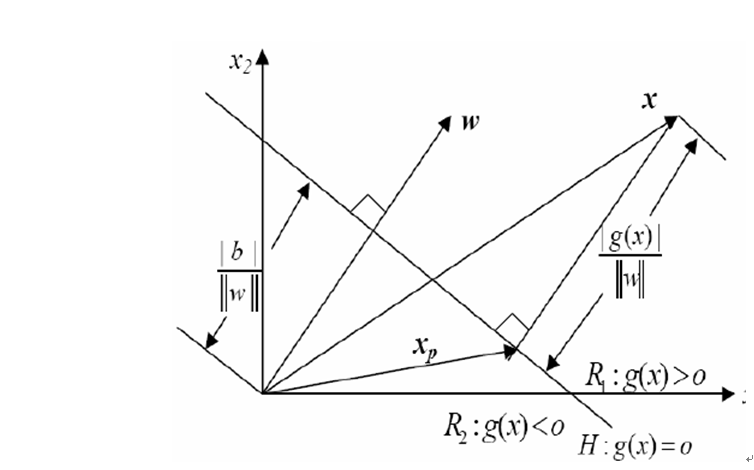
一個點到分割面的距離，稱為點相對於分割面的距離。

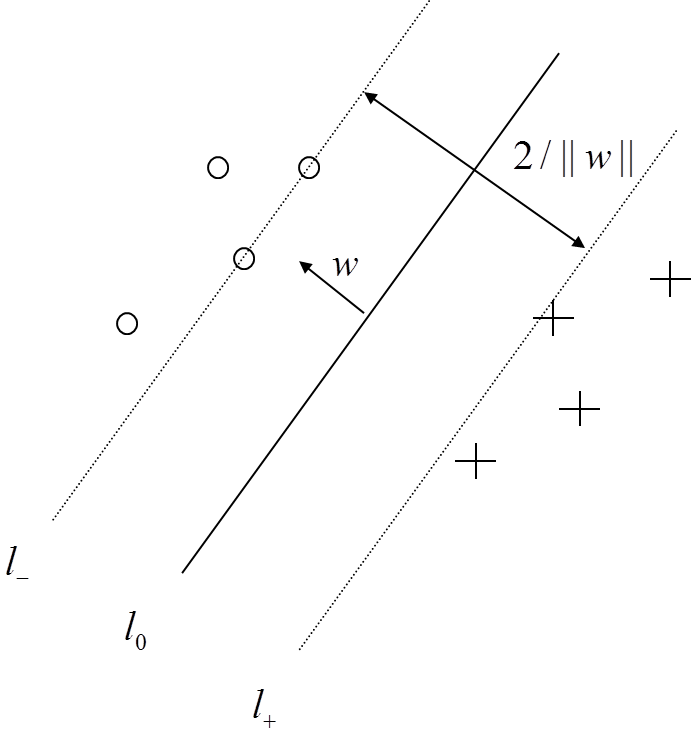
資料集中所有的點到分割面的最小間隔的2倍，稱為分類器或資料集的間隔。

最大間隔：SVM分類器是要找最大的資料集間隔。

支援向量：離分割超平面最近的那些點。

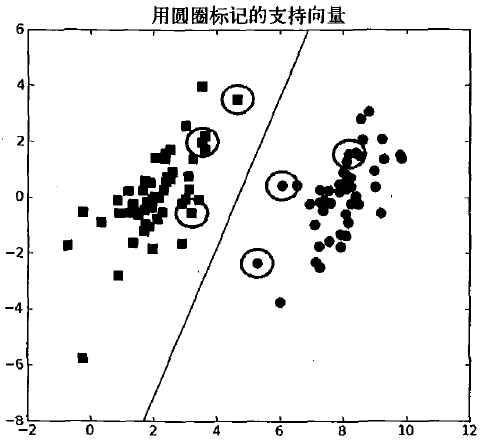
SVM演算法其實就是最大化支援向量到分割面的距離。另外，目前上面講的都是針對線性可分的資料集。非線性的資料集，需要核函式轉換空間，才具有非線性資料處理能力。

最優分類超平面只由少數支援向量決定，問題具有稀疏性。

二、推導

下面講解下SVM的數學原理，其實就是複述我之前寫過的東西。

（這裡yi(wTx+b)稱為點到分割面的函式間隔。yi(wT

            現在的目標就是找出分類器定義中的w和b。為此，我們必須找到具有最小間隔的資料點，而這些資料點也就是前面提到的支援向量。一旦找到具有最小間隔的資料點，我們就需要對該間隔最大化。這就可以寫作：

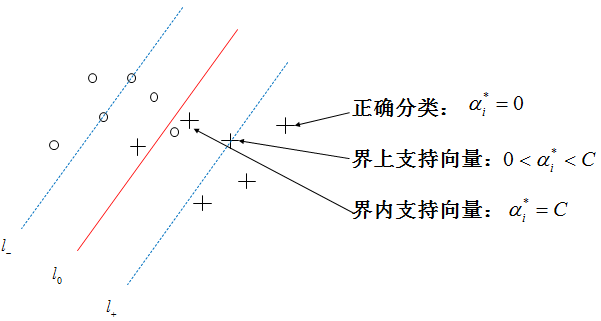
          直接求解上面的公式很難。並且到目前為止，我們知道所有數都不那麼幹淨，不能100%線性可分。我們可以通過引入鬆弛變數，來允許有些資料點可以處於分割面的錯誤的一側。如下面幾幅圖所示：

 εi是鬆弛變數，常數C代表懲罰係數，即如果某個x是屬於某一類，但是它偏離了該類，跑到邊界上後者其他類的地方去了，C越大表明越不想放棄這個點，邊界就會縮小，錯分點更少，但是過擬合情況會比較嚴重。

為此，我們引入拉格朗日乘子，用條件極值求解最優分介面，構造拉格朗日函式，也是之前公式(3)的對偶形式：

也就是說，只要求的拉格朗日乘子ai，我們就能得到分類邊界。

三、序列最小化方法SMO

    C-SVM是一個凸二次規劃問題，SMO演算法能快速解決SVM的二次規劃問題，把它分解成一些子問題來解決。在每一步中，SMO演算法僅選擇兩個拉格朗日乘子進行優化，然後再更新SVM以反應新的優化值。

   對於C-SVM目標函式和優化過程中必須遵循的約束條件如下：

現在打算自己用smo演算法實現，下面就重點講下smo演算法。

       C-SVM的KTT條件為：

(KTT條件是指在滿足一些有規則的條件下, 一個非線性規劃(Nonlinear Programming)問題能有最優化解法的一個必要和充分條件.即最優解都需要滿足KTT條件)。現在這裡對於C-SVM的KTT條件為：

其中，b*由上面的公式計算得到。

SMO演算法包括兩個步驟：一是用分析的方法解一個簡單的優化問題；二是選擇待優化的拉格朗日乘子的策略。

(1)   簡單的優化問題----兩個拉格朗日乘子優化問題的解

    現在，在一條線段上求目標函式的極值，相當於一個一維的極值問題。我們可以把a1用a2表示，對a2求無條件極值，如果目標函式是嚴格凹的，最小值就一定在這一極值點(極值點在區間內)或在區間端點(極值點在區間外)。a2確定下來後，a1也確定了。因此，我們要先找到a2的優化區間，再在這個區間中對a2求最小值。

根據上面兩幅圖可以知道，a2優化區間：

當y1和y2異號時：【L、H的計算是由a2-a1正負未知所導致的】

當y1和y2同號時：

(b)當L的二階導數為0，即訓練樣本中出現相同的特徵時，我們計算目標函式是單調的。最小值線上段兩個端點上的取值，我們將a2=L和a2=H分別代入目標函式，這樣拉格朗日乘子就修正到目標函式較小的端點上，比較ΨL和ΨH就可以求得Ψ的最小值。最終得到a2的值，接著一串值都解出來了。

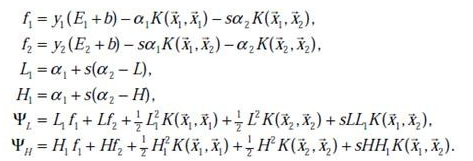
至於偏置值b，每一步都要更新，因為前面的KKT條件指出了ai和yiui關係，而ui和b有關，在每一步計算出ai後，根據KKT條件來調整b，分如下幾種情況

(2)   選擇策略----選取兩個拉格朗日乘子的啟發規則

事實上即使我們不採用任何找點法，只是按順序抽取ai，aj的所有組合進行優化，目標函式也會不斷下降。直到任一對ai，aj都不能繼續優化，目標函式就會收斂到極小值。我們採取某種找點方法只是為了使演算法收斂得更快。

這種試探法先選擇最有可能需要優化的a2，再針對這樣的a2選擇最有可能取得較大修正步長的a1。這樣，我們在程式中使用兩個層次的迴圈：

外層迴圈首先遍歷所有樣本查詢違反KTT規則的乘子進行優化，當完成一次遍歷後外層迴圈再遍歷那些非邊界乘子的樣本(0<a<C)，挑選那些違反KTT條件的樣本進行優化。外層迴圈重複執行，直到所有的非邊界樣本在一定範圍內均滿足KKT條件。

    在選定第一個拉格朗日乘子ai後，內層迴圈會通過最大化步長的方式來挑選第二個拉格朗日乘子，即最大化|Ei-Ej|,當Ei為正時最小化Ej，當為負Ei時最大化Ej.

下面給出matlab程式碼實現 ：

本次內容主要講解什麼是支援向量，SVM分類是如何推導的，最小序列SMO演算法部分推導。

最後給出線性和非線性2分類問題的smo演算法matlab實現程式碼。

一、什麼是支援向量機(Support Vector Machine)

本節內容部分翻譯Opencv教程：

SVM是一個由分類超平面定義的判別分類器。也就是說給定一組帶標籤的訓練樣本，演算法將會輸出一個最優超平面對新樣本(測試樣本)進行分類。

什麼樣的超平面才是最優的？我們考慮如下場景：對於一個由二維座標點構成的線性可分集合，如何找到一條直線將兩類座標分隔開？

      上圖中，你可以看到存在多條直線將兩類座標分開。它們中有沒有最好的？我們可以直觀地定義如下規則：如果一條分割的直線離座標點太近，那它就不是最佳的。因為它會對噪聲敏感，不能正確的推廣。因此，我們的目標是找到一條分割線，它要離所有的樣本點都儘可能的遠。

       SVM演算法就是找一個超平面，並且它到離他最近的訓練樣本的距離要最大。即最優分割超平面最大化訓練樣本邊界。

原諒哥的翻譯水平，看著自己也彆扭，重新整理下：

對線性可分集，總能找到使樣本正確劃分的分介面，而且有無窮多個，哪個是最優？ 必須尋找一種最優的分界準則，是兩類模式分開的間隔最大。

在介紹如何推到之前，瞭解一個定義：

分隔超平面：上述將資料集分割開來的直線叫做分隔超平面。

超平面：如果資料集是N維的，那麼就需要N-1維的某物件來對資料進行分割。該物件叫做超平面，也就是分類的決策邊界。

間隔：

一個點到分割面的距離，稱為點相對於分割面的距離。

資料集中所有的點到分割面的最小間隔的2倍，稱為分類器或資料集的間隔。

最大間隔：SVM分類器是要找最大的資料集間隔。

支援向量：離分割超平面最近的那些點。

SVM演算法其實就是最大化支援向量到分割面的距離。另外，目前上面講的都是針對線性可分的資料集。非線性的資料集，需要核函式轉換空間，才具有非線性資料處理能力。

最優分類超平面只由少數支援向量決定，問題具有稀疏性。

二、推導

下面講解下SVM的數學原理，其實就是複述我之前寫過的東西。

（這裡yi(wTx+b)稱為點到分割面的函式間隔。yi(wTx+b)/|w|稱為點到分割面的幾何間隔）

            現在的目標就是找出分類器定義中的w和b。為此，我們必須找到具有最小間隔的資料點，而這些資料點也就是前面提到的支援向量。一旦找到具有最小間隔的資料點，我們就需要對該間隔最大化。這就可以寫作：

          直接求解上面的公式很難。並且到目前為止，我們知道所有數都不那麼幹淨，不能100%線性可分。我們可以通過引入鬆弛變數，來允許有些資料點可以處於分割面的錯誤的一側。如下面幾幅圖所示：

 εi是鬆弛變數，常數C代表懲罰係數，即如果某個x是屬於某一類，但是它偏離了該類，跑到邊界上後者其他類的地方去了，C越大表明越不想放棄這個點，邊界就會縮小，錯分點更少，但是過擬合情況會比較嚴重。

為此，我們引入拉格朗日乘子，用條件極值求解最優分介面，構造拉格朗日函式，也是之前公式(3)的對偶形式：

也就是說，只要求的拉格朗日乘子ai，我們就能得到分類邊界。

三、序列最小化方法SMO

    C-SVM是一個凸二次規劃問題，SMO演算法能快速解決SVM的二次規劃問題，把它分解成一些子問題來解決。在每一步中，SMO演算法僅選擇兩個拉格朗日乘子進行優化，然後再更新SVM以反應新的優化值。

   對於C-SVM目標函式和優化過程中必須遵循的約束條件如下：

現在打算自己用smo演算法實現，下面就重點講下smo演算法。

       C-SVM的KTT條件為：

(KTT條件是指在滿足一些有規則的條件下, 一個非線性規劃(Nonlinear Programming)問題能有最優化解法的一個必要和充分條件.即最優解都需要滿足KTT條件)。現在這裡對於C-SVM的KTT條件為：

其中，b*由上面的公式計算得到。

SMO演算法包括兩個步驟：一是用分析的方法解一個簡單的優化問題；二是選擇待優化的拉格朗日乘子的策略。

(1)   簡單的優化問題----兩個拉格朗日乘子優化問題的解

    現在，在一條線段上求目標函式的極值，相當於一個一維的極值問題。我們可以把a1用a2表示，對a2求無條件極值，如果目標函式是嚴格凹的，最小值就一定在這一極值點(極值點在區間內)或在區間端點(極值點在區間外)。a2確定下來後，a1也確定了。因此，我們要先找到a2的優化區間，再在這個區間中對a2求最小值。

根據上面兩幅圖可以知道，a2優化區間：

當y1和y2異號時：【L、H的計算是由a2-a1正負未知所導致的】

當y1和y2同號時：

(b)當L的二階導數為0，即訓練樣本中出現