1.影象處理方法分類

輸入	輸出	等級	例子
影象	影象	初級	降噪，增強對比度
影象	影象特徵	中級	輪廓提取
影象	影象表徵的資訊	高階	模式識別，機器視覺

2. 影象增強(image enhancement)

1. 沒有統一的影象增強演算法，要針對具體問題具體分析，使用者是最終標準的評判者；使用者說好就是好，所以沒有所謂”最好 ”的影象增強演算法。

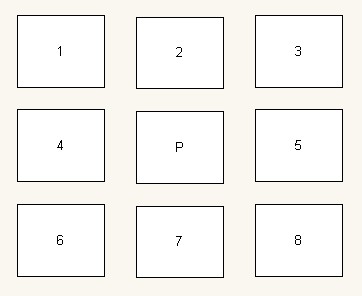
3. 畫素點之間的關係

名稱	表示法	包括點
4鄰域（4-neightbors）	N4(p)	{2,4,5,7}
D鄰域(d-neightbors)	ND (p)	{1,3,6,8}
8鄰域(8-neightbors)	N8(p)	{1,2,3,4,5,6,7,8}

4. 鄰接(adjacency)、連通(connectivity)、區域(regions) 、邊界(boundaries)

4.1 鄰接

鄰接有的書上翻譯叫連線，其實是一個意思。這就體現了看英文資料的好處，沒有翻譯導致的奇異。
設f(p)” role=”presentation” style=”position: relative;”>f

(p)f(p)全體值域的y一個子集，則

名稱	定義
4鄰接(4-adjacency)	f(p)∈V∧f(q)∈V∧q∈N4(p)” role=”presentation” style=”position: relative;”>f(p)∈V∧f(q)∈V∧q∈N4(p)f(p)∈V∧f(q)∈V∧q∈N4(p)
8鄰接(8-adjacency	f(p)∈V∧f(q)∈V∧q∈N8(p)” role=”presentation” style=”position: relative;”>f(p)∈V∧f(q)∈V∧q∈N8(p)f(p)∈V∧f(q)∈V∧q∈N8(p)
m鄰接(m-adjacency)	1.f(p)∈V∧f(q)∈V” role=”presentation” style=”position: relative;”>f(p)∈V∧f(q)∈Vf(p)∈V∧f(q)∈V

m鄰接又稱為混合鄰接，其作用是為了消除8鄰接導致的多路問題。
為了解釋這個多路問題，需要引入路徑的概念。路徑(path）是一系列畫素點的集合，相鄰的倆個畫素點的關係要滿足一種鄰接的定義。比如4鄰接路徑，就表示路徑中相鄰兩個畫素點滿足4鄰接關係。8鄰接路徑、m鄰接路徑的定義與此類似。
假設V={1},則各種鄰接的路徑如下圖所示：

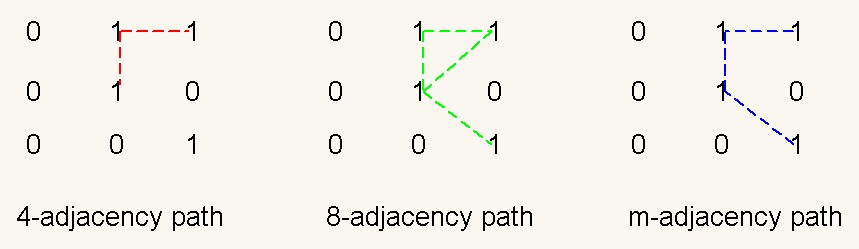
可以看出8鄰接路徑存在多路的問題。

4.2 連通

設S為影象中部分畫素的集合
如果可以在S中找到一條路徑連線畫素點p和q，則稱p和q 在S中是連通的。自然，根據路徑選擇方法的不同，連通也應該分為4連通，8連通和m連通。
在S中，對於任意的畫素點p，所有與p點連通的畫素點的集合（包括p點）稱為一個連通元件。如果在S中只能找到一個連通元件，則稱S為連通集合。

4.3 區域

影象中的一個連通集合也可以叫做一個區域。自然，依據使用的連通型別不同，區域也分為4連通區域，8連通區域（原則上講也應該有m連通區域，但在涉及區域的問題討論中很少應用m連通）。
如果兩個4連通區域可以合併為一個更大的4連通區域，則稱這兩個區域是4鄰接的。相應的，也存在8鄰接。
如果兩個型別相同的連通區域無法合併，則稱這兩個連通區域是不想交的（disjoint）。
ps:在同一副影象上劃分區域時，只會採用一種連通型別。要麼都是4連通的，要麼都是8連通的。不會出現我把影象的左邊劃分為4連通的，右邊劃分為8連通的情況。

4.4 前景(foreground)和背景(background)

假設在一副影象上有k個不想交的區域。
設R_u等於所有者k個區域的集合，(R_u)^c等於影象上R_u以外的畫素點的集合。
則，R_u稱為影象的前景，(R_u)^c稱為R_u的背景。（這個相對性很重要，背景是針對前景而言的）

4.5 邊界(boundary,border)

如果區域R中存在畫素點p，且p點的領域中至少有一個畫素點落在R的背景中，則R中所有這樣的點P組成的集合叫做區域R的邊界。
根據上面的定義，自然也存在4連通邊界和8連通邊界的說法。但更多使用的是8連通邊界，否則如下圖中紅圈圈出的點將不被認為是邊界，這很不自然。

以上方式定義的區域的內邊界，響應的，在背景中與內邊界相鄰的點組成的集合稱為外邊界。

5. 距離

兩個畫素點間的距離計算方式，常見的有三種，定義如下:

De(p,q)=(p.x−q.x)2+(p.y−q.y)2” role=”presentation” style=”position: relative;”>De(p,q)=(p.x−q.x)2+(p.y−q.y)2−−−−−−−−−−−−−−−−−−−−−−√De(p,q)=(p.x−q.x)2+(p.y−q.y)2

D4(p,q)=|p.x−q.x|+|p.y−q.y|” role=”presentation” style=”position: relative;”>D4(p,q)=|p.x−q.x|+|p.y−q.y|D4(p,q)=|p.x−q.x|+|p.y−q.y|

D8(p,q)=max(|p.x−q.x|,|p.y−q.y|)” role=”presentation” style=”position: relative;”>D8(p,q)=max(|p.x−q.x|,|p.y−q.y|)D8(p,q)=max(|p.x−q.x|,|p.y−q.y|)

6. gamma校正

6.1 gamma校正的定義

首先介紹一下變換函式

S=crγ” role=”presentation” style=”text-align: center; position: relative;”>S=crγS=crγ S = cr^\gamma
其中
r—某個畫素點的強度；
c—為嘗試；
γ” role=”presentation” style=”position: relative;”>γγ—為變換引數；
s—此畫素點變換後的強度；
利用以上公式對輸入影象的每個畫素點進行處理的過程稱為gamma校正。

6.2 gamma校正的作用

1.修復影象失真

下圖展示了一副自然界影象經電子裝置呈現在人眼上的過程

如果自然界影象經過感測器直接轉化為數字影象時，會發生失真。這種失真是由於感測器硬體引起的，無法避免。經驗上可以將失真總結為如下的形式：

数字图像像素(x,y)=（自然界图像(x,y)）α” role=”presentation” style=”text-align: center; position: relative;”>數字圖像像素(x,y)=（自然界圖像(x,y)）α數字影象畫素(x,y)=（自然界影象(x,y)）α 數字影象畫素(x,y) = （自然界影象(x,y)）^\alpha
為了彌補這種失真，可以在步驟2增加一部gamma校正，即:
数字图像像素(x,y)=gamma校正(（自然界图像(x,y)）α)” role=”presentation” style=”text-align: center; position: relative;”>數字圖像像素(x,y)=gamma校正(（自然界圖像(x,y)）α)數字影象畫素(x,y)=gamma校正(（自然界影象(x,y)）α) 數字影象畫素(x,y) = gamma校正(（自然界影象(x,y)）^\alpha)
gamma校正(r)=r1α” role=”presentation” style=”text-align: center; position: relative;”>gamma校正(r)=r1αgamma校正(r)=r1α gamma校正(r) = r^\frac{1}{\alpha}
經過這樣的校正，數字影象和自然界影象就相同了。
可以看出，校正的關鍵是 α” role=”presentation” style=”position: relative;”>αα值的選擇。這個值一般由感測器的生成廠家根據自身產品的特點固化在感測器裡，對感測器的使用者來說，是不需要關係的。

2.增加對比度

下圖展示了不同γ” role=”presentation” style=”position: relative;”>γγ下，輸入與輸出的關係

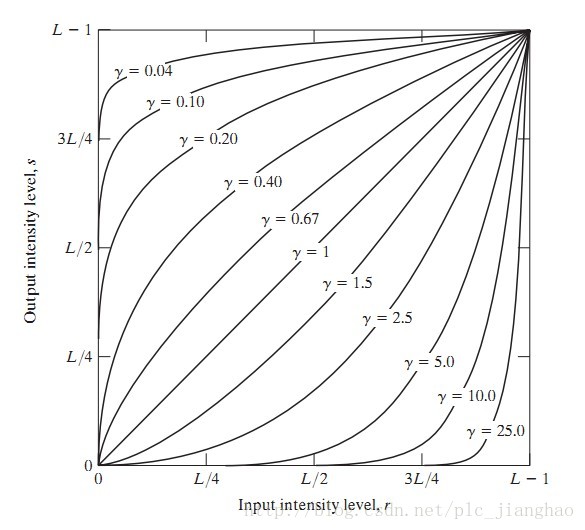
可以看出當&#x03B3;&lt;1” role=”presentation” style=”position: relative;”>γ<1γ<1時，會增強原影象中暗處的對比度；
可以看出當&#x03B3;==1” role=”presentation” style=”position: relative;”>γ==1γ==1時，無任何效果；
可以看出當&#x03B3;&gt;1” role=”presentation” style=”position: relative;”>γ>1γ>1時，會增強原影象中亮處的對比度；
但是對強度的影響是非線性的。

7. 灰度分層（intensity-level slicing）

8.Bit平面分層(bit-plane slicing)

概念上比較抽象，舉個例子來理解。
假設每一個畫素點由2bit組成，一副影象有4個畫素點。則如下圖所示，影象1可以由影象2和影象3疊加而來。

那麼，影象2和影象3就是影象1的兩個bit平面。
同理可以推斷出，如果每個畫素點由8個bit組成，則一副影象應該有8個bit平面。
bit平面分層可以用於影象的有失真壓縮，通過這種分析你可以發現，有些bit平面對影象的貢獻是很小的，刪除這一層的資料，人眼是無法分辨的，但這樣就節約了空間以及傳輸的資料量。

9.直方圖(histogram)處理

1.影象的直方圖

影象的直方圖實際上就是影象不同強度的畫素點的概率分佈圖。
假設一副8bit影象（8bit影象指影象的每個畫素點用8bit長度的資料表示，共可以表示0~255，共計256個強度）有M*N個畫素點。
令n₂₅₅表示強度的255的點，在影象中的數量，則此影象強度為255的概率可根據如下公式計算：

P255=n255M&#x2217;N” role=”presentation” style=”text-align: center; position: relative;”>P255=n255M∗NP255=n255M∗N P_{255} = \frac{n_{255}}{M*N}
同理可以計算出P ₀~P ₂₅₅的值，然後以強度為x軸，概率為y軸繪製的直方圖，就是此影象的直方圖。
通過影象的直方圖可以看出以下幾點結論：
1. 影象亮度較暗，則直方圖集中在x軸的左側；
2. 影象亮度較亮，則直方圖集中在x軸的右側；
3. 影象對比度較低，則直方圖集中在某個很小的範圍內；
4. 影象對比度較高，則直方圖均勻分佈在整個x軸。

2.直方圖均衡

根據上一節的結論4，“影象對比度較高，則直方圖均勻分佈在整個x軸”。我們可以將一個對比度較低的影象，通過某種變化，使其直方圖均勻分佈，這樣就可以增進對比度。這其中最簡單的演算法是“直方圖均衡”。
令s=T(r)” role=”presentation” style=”position: relative;”>s=T(r)s=T(r)是連續可微函式，則有如下結論：

Ps(s)=Pr(r)|drds|” role=”presentation” style=”text-align: center; position: relative;”>Ps(s)=Pr(r)∣∣∣drds∣∣∣Ps(s)=Pr(r)|drds| 必須是 “連續可微”函式。
基於以上的結論，我們可以構造如下的轉換函式：
T(r)=(N&#x2212;1)&#x222B;0rPr(w)dw” role=”presentation” style=”text-align: center; position: relative;”>T(r)=(N−1)∫r0Pr(w)dwT(r)=(N−1)∫0rPr(w)dw
基於以上構造的轉換函式，我們很容易計算出 Ps(s)=1N&#x2212;1” role=”presentation” style=”text-align: center; position: relative;”>Ps(s)=1N−1Ps(s)=1N−1 ,即轉換後，所有的畫素點的概率分佈為常數，對比度最大。

3.自由選擇輸出影象的概率密度函式

上一節中構造的轉換函式，轉換後圖像的概率密度是常數。這在多數情況下已經足夠好，但有時我們希望自由選擇輸出影象的概率密度函式。
下面直接介紹演算法：
1. 令變換後的概率密度函式為Pz(z)” role=”presentation” style=”position: relative;”>Pz(z)Pz(z);
2. 令s1=(N&#x2212;1)&#x222B;0zPz(w)dw” role=”presentation” style=”position: relative;”>s1=(N−1)∫z0Pz(w)dws1=(N−1)∫0zPz(w)dw；
3. 由於Pr(r)” role=”presentation” style=”position: relative;”>Pr(r)Pr(r)的對應關係表；
4. 由於Pz(z)” role=”presentation” style=”position: relative;”>Pz(z)Pz(z)的對應關係表；
5. 基於以上幾點可知，當有一個輸入r” role=”presentation” style=”position: relative;”>rr，即完成了變換。

        <link rel="stylesheet" href="https://csdnimg.cn/release/phoenix/template/css/markdown_views-ea0013b516.css">
            </div>

1.影象處理方法分類

輸入	輸出	等級	例子
影象	影象	初級	降噪，增強對比度
影象	影象特徵	中級	輪廓提取
影象	影象表徵的資訊	高階	模式識別，機器視覺

2. 影象增強(image enhancement)

1. 沒有統一的影象增強演算法，要針對具體問題具體分析，使用者是最終標準的評判者；使用者說好就是好，所以沒有所謂”最好 ”的影象增強演算法。

3. 畫素點之間的關係

名稱	表示法	包括點
4鄰域（4-neightbors）	N4(p)	{2,4,5,7}
D鄰域(d-neightbors)	ND(p)	{1,3,6,8}
8鄰域(8-neightbors)	N8(p)	{1,2,3,4,5,6,7,8}

4. 鄰接(adjacency)、連通(connectivity)、區域(regions) 、邊界(boundaries)

4.1 鄰接

鄰接有的書上翻譯叫連線，其實是一個意思。這就體現了看英文資料的好處，沒有翻譯導致的奇異。
設f(p)” role=”presentation” style=”position: relative;”>f(p)f(p)全體值域的y一個子集，則

名稱	定義
4鄰接(4-adjacency)	f(p)∈V∧f(q)∈V∧q∈N4(p)” role=”presentation” style=”position: relative;”>f(p)∈V∧f(q)∈V∧q∈N4(p)f(p)∈V∧f(q)∈V∧q∈N4(p)
8鄰接(8-adjacency	f(p)∈V∧f(q)∈V∧q∈N8(p)” role=”presentation” style=”position: relative;”>f(p)∈V∧f(q)∈V∧q∈N8(p)f(p)∈V∧f(q)∈V∧q∈N8(p)
m鄰接(m-adjacency)	1.f(p)∈V∧f(q)∈V” role=”presentation” style=”position: relative;”>f(p)∈V∧f(q)∈Vf(p)∈V∧f(q)∈V

m鄰接又稱為混合鄰接，其作用是為了消除8鄰接導致的多路問題。
為了解釋這個多路問題，需要引入路徑的概念。路徑(path）是一系列畫素點的集合，相鄰的倆個畫素點的關係要滿足一種鄰接的定義。比如4鄰接路徑，就表示路徑中相鄰兩個畫素點滿足4鄰接關係。8鄰接路徑、m鄰接路徑的定義與此類似。
假設V={1},則各種鄰接的路徑如下圖所示：

可以看出8鄰接路徑存在多路的問題。

4.2 連通

設S為影象中部分畫素的集合
如果可以在S中找到一條路徑連線畫素點p和q，則稱p和q 在S中是連通的。自然，根據路徑選擇方法的不同，連通也應該分為4連通，8連通和m連通。
在S中，對於任意的畫素點p，所有與p點連通的畫素點的集合（包括p點）稱為一個連通元件。如果在S中只能找到一個連通元件，則稱S為連通集合。

4.3 區域

影象中的一個連通集合也可以叫做一個區域。自然，依據使用的連通型別不同，區域也分為4連通區域，8連通區域（原則上講也應該有m連通區域，但在涉及區域的問題討論中很少應用m連通）。
如果兩個4連通區域可以合併為一個更大的4連通區域，則稱這兩個區域是4鄰接的。相應的，也存在8鄰接。
如果兩個型別相同的連通區域無法合併，則稱這兩個連通區域是不想交的（disjoint）。
ps:在同一副影象上劃分區域時，只會採用一種連通型別。要麼都是4連通的，要麼都是8連通的。不會出現我把影象的左邊劃分為4連通的，右邊劃分為8連通的情況。

4.4 前景(foreground)和背景(background)

假設在一副影象上有k個不想交的區域。
設R_u等於所有者k個區域的集合，(R_u)^c等於影象上R_u以外的畫素點的集合。
則，R_u稱為影象的前景，(R_u)^c稱為R_u的背景。（這個相對性很重要，背景是針對前景而言的）

4.5 邊界(boundary,border)

如果區域R中存在畫素點p，且p點的領域中至少有一個畫素點落在R的背景中，則R中所有這樣的點P組成的集合叫做區域R的邊界。
根據上面的定義，自然也存在4連通邊界和8連通邊界的說法。但更多使用的是8連通邊界，否則如下圖中紅圈圈出的點將不被認為是邊界，這很不自然。

以上方式定義的區域的內邊界，響應的，在背景中與內邊界相鄰的點組成的集合稱為外邊界。

5. 距離

兩個畫素點間的距離計算方式，常見的有三種，定義如下:

De(p,q)=(p.x&#x2212;q.x)2+(p.y&#x2212;q.y)2” role=”presentation” style=”position: relative;”>De(p,q)=(p.x−q.x)2+(p.y−q.y)2−−−−−−−−−−−−−−−−−−−−−−√De(p,q)=(p.x−q.x)2+(p.y−q.y)2

D4(p,q)=|p.x&#x2212;q.x|+|p.y&#x2212;q.y|” role=”presentation” style=”position: relative;”>D4(p,q)=|p.x−q.x

相關推薦