計算機圖形學(四)幾何變換_4_二維複合變換_5_其他二維變換_2_錯切
阿新 • • 發佈:2019-01-02
二維複合變換_5_其他二維變換_2_錯切
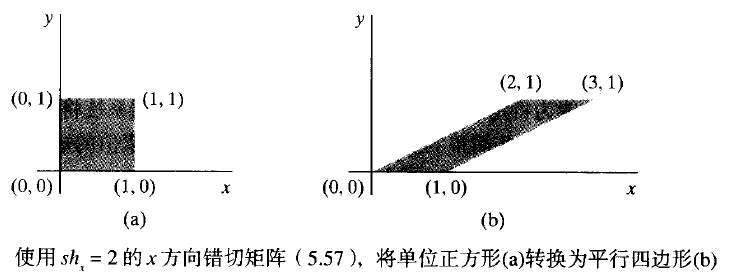
錯切(shear)是一種使物件形狀發生變化的變換,經過錯切的物件好像是由已經相互滑動的內部夾層組成。兩種常用的錯切變換是移動x座標值的錯切和移動Y座標值的錯切。相對於x軸的x方向錯切由下列變換矩陣1產生:
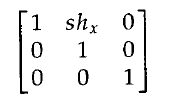
該矩陣將座標位置轉換成
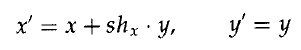
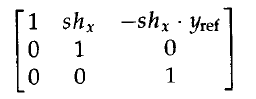
現在,座標位置將變換為
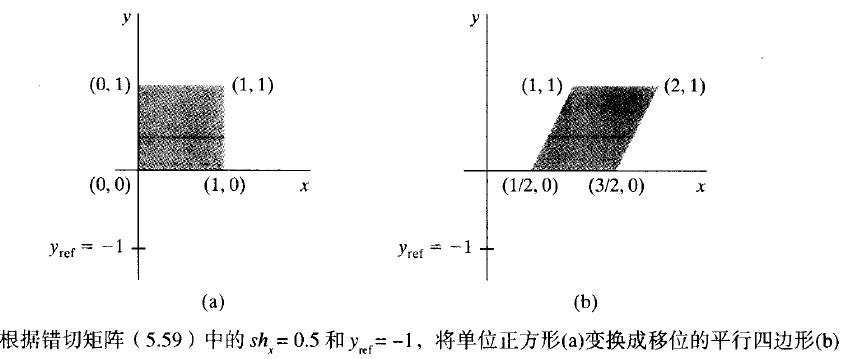
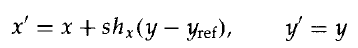 下圖中給出了錯切引數為1/2,相對於直線yref
下圖中給出了錯切引數為1/2,相對於直線yref
使用下列變換矩陣3生成相對於線x = xref 的y方向錯切:
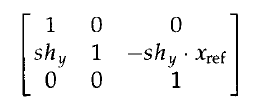
該矩陣生成變換的座標位置:
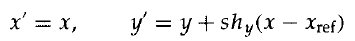
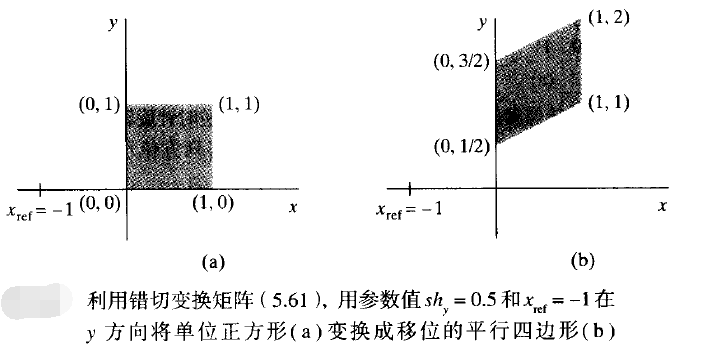
這種變換根據正比於其到參考線x = xref距離的量而垂直地改變座標位置。如下圖給出使用shy = 0.5和xref = -1將正方形轉換成平行四邊形。
錯切操作可以表示為基本變換的序列。例如,x方向的錯切矩陣可以寫為複合變換矩陣,包含一系列旋轉和沿對角線縮放中的單位正方形的縮放矩陣,同時保持了邊的原始長度以及與x軸的平行性。在相對於錯切參考線的物件位置處的移位等價於平移。
錯切(shear)是一種使物件形狀發生變化的變換,經過錯切的物件好像是由已經相互滑動的內部夾層組成。兩種常用的錯切變換是移動x座標值的錯切和移動Y座標值的錯切。相對於x軸的x方向錯切由下列變換矩陣1產生:
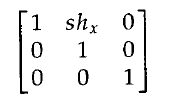
該矩陣將座標位置轉換成
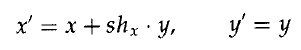
可以將任意實數賦給錯切引數shx。然後將座標位置(x, y)水平地移動與其到x軸(y = 0)的距離(Y值)成正比的量。例如,設定shx為2,如下圖將正方形變為平行四邊形。shx為負值則將座標位置向左移動。
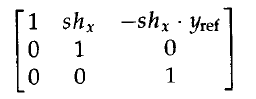
現在,座標位置將變換為
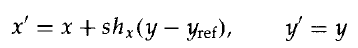 下圖中給出了錯切引數為1/2,相對於直線yref
下圖中給出了錯切引數為1/2,相對於直線yref
使用下列變換矩陣3生成相對於線x = xref 的y方向錯切:
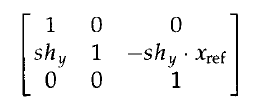
該矩陣生成變換的座標位置:
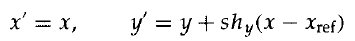
這種變換根據正比於其到參考線x = xref距離的量而垂直地改變座標位置。如下圖給出使用shy = 0.5和xref = -1將正方形轉換成平行四邊形。

錯切操作可以表示為基本變換的序列。例如,x方向的錯切矩陣可以寫為複合變換矩陣,包含一系列旋轉和沿對角線縮放中的單位正方形的縮放矩陣,同時保持了邊的原始長度以及與x軸的平行性。在相對於錯切參考線的物件位置處的移位等價於平移。