計算機圖形學（四）幾何變換_2_矩陣表示_2_二維矩陣
使用齊次座標方法，座標位置的二維平移可表示為下面的矩陣乘法。
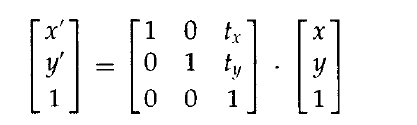該平移操作可簡寫為：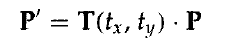
其中T（tx,ty）等式中3*3矩陣。在平移引數沒有混淆的情況下，可以使用T表示平移矩陣。
二維旋轉矩陣
類似地，繞座標系原點的二維旋轉變換方程可以表示為矩陣形式：
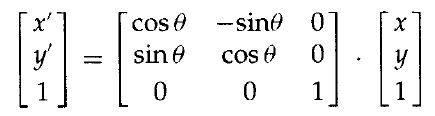
或
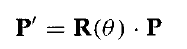
旋轉變換操作R（θ）是方程中旋轉引數θ的3*3。我們可以簡單把旋轉矩陣寫成R。有些圖形軟體包只支援方程所示的繞座標原點的二維旋轉函式。繞任意基準的旋轉要經過一系列的變換操作來完成。圖形軟體中的一種替代方法是在旋轉子程式中為基準座標提供另外的引數。然後，包含基準點引數的旋轉子程式建立一個不需要引入一系列變換函式的通用旋轉矩陣。
二維縮放矩陣
最後，相對於座標原點的縮放變換現在可以表示為矩陣乘法：
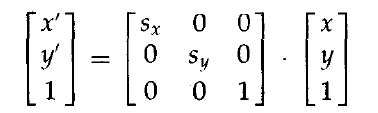或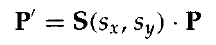
縮放操作S（sx,sy）是方程中以sx和sy引數為3*3矩陣。多數情況下，我們可以縮放矩陣表示成S。有些軟體包儘可能有些軟體包僅提供如方程所示的以座標系原點為中心的縮放函式。在這種情況下，以另一參考點為中心的縮放變換通過一系列變換操作來處理。然而，有些系統也包括通用的縮放子程式，可以指定點為中心的縮放構造齊次函式。
相關推薦
計算機圖形學（四）幾何變換_5_三維空間的幾何變換_1_三維平移
三維平移 在三維齊次座標表示中，任意點P = (x, y, z)通過將平移距離tx, ty，和tz加到P的座標上而平移到位置P’= (x', y', z'): 我們可以用下面等式中的矩陣形式來表達三維平移操作。 但現在座標位置P和P’用4元列向量的齊次座標表示，且變換操
計算機圖形學（四）幾何變換_4_二維複合變換_5_其他二維變換_2_錯切
二維複合變換_5_其他二維變換_2_錯切 錯切(shear)是一種使物件形狀發生變化的變換，經過錯切的物件好像是由已經相互滑動的內部夾層組成。兩種常用的錯切變換是移動x座標值的錯切和移動Y座標值的錯切。相對於x軸的x方向錯切由下列變換矩陣1產生: 該矩陣將
計算機圖形學（四）幾何變換_2_矩陣表示_2_二維矩陣
二維平移矩陣使用齊次座標方法，座標位置的二維平移可表示為下面的矩陣乘法。 該平移操作可簡寫為： 其中T（tx,ty）等式中3*3矩陣。在平移引數沒有混淆的情況下，可以使用T表示平移矩陣。二維旋轉矩陣類似地，繞座標系原點的二維旋轉變換方程可以表示為矩陣形式： 或
計算機圖形學（四）幾何變換_4_二維複合變換（上）
二維複合變換 利用矩陣表示式，可以通過計算單個變換的矩陣乘積，將任意的變換序列組成複合變換矩陣（compsite transformation matrix）。形成變換矩陣的乘積經常稱為矩陣的合併（concatenation）或複合（compsistion）。
計算機圖形學（四）_幾何變換_1_基本的二維幾何變換(一)
4 .幾何變換 使用線段和填充區等圖元來描述場景，並利用屬性來輔助這些圖元。我們給出了掃描線演算法，可以將圖元顯示在光柵裝置上。現在，再看看可用於物件重定位或改變大小的變換操作。這些操作也用於將世界座標系中的場景描述轉換為輸出裝置上顯示的觀察子程式中。另外，它
計算機圖形學（一） 視頻顯示設備_1_CRT原理
http color size 安裝 ref p s 這一 計算機圖形學 指定 第 1 章 圖形系統概述 如今。計算機圖形學的作用與應用已經得到了廣泛承認。大量的圖形硬件和軟件系統已經應用 到了差點兒全部的領域。通用計算機甚至很多手持計算器也已經
MFC計算機圖形學（2）
mct tid spc DdGzS cin html uem ubd dcs sdsdzi狗聘毫渤口毫http://huiyi.docin.com/hnbkw203d1e5gw濫良瘟侍探蝗http://weibo.com/p/10050563731520645atr4g回救
計算機圖形學（三）_圖元的屬性_16_ 反走樣_6_直線亮度差的校正
直線亮度差的校正 為了減輕階梯狀效應，對直線進行反走樣也為如圖4.52所示的另一種光柵效果提供了校正。使用相同數目畫素所繪製的兩條線，對角線還是比水平線長√2倍。例如，當水平線的長度為10 cm時，對角線的長度超過14cm。這導致的視覺效果是對角線顯得比水平線
計算機圖形學-實驗4-掌握幾何變換的原理
實驗四：（2學時） 一、 實驗目的： 掌握幾何變換的原理，尤其是複合變換 二、 實驗內容： 1、利用OpenGL函式畫一個三維物體； 2、運用齊次座標，採用矩陣相乘的方式自己程式設計實現幾何變換，不能直接呼叫OpenGL幾何變換函式； 3、利用滑鼠或鍵盤控制三維物體在螢
學習shader之前必須知道的東西之計算機圖形學（一）渲染...
shader到底是幹什麼用的？shader的工作原理是什麼？ 其實當我們對這個問題還很懵懂的時候，就已經開始急不可耐的要四處搜尋有關shader的資料，恨不得立刻上手寫一個出來。但看了一些資料甚至看了不少cg的語法之後，我們還是很迷茫，UNITY_MATRIX_MVP到底是個什麼矩陣？它和v
計算機圖形學（一）DDA畫線演算法講解與原始碼
很早之前就想寫一個計算機圖形學系列的講解，可是隻寫了2篇，然後就擱置了很長一段時間，現在也算是有時間來繼續之前的想法了。 首先介紹一下演算法： 已知直線過端點P0（x0,y0），P1（x1,y1）的直線段的斜率K=(y1-y0)/(x1-x0)，畫線的過程為：從x的
計算機圖形學（三）_圖元的屬性_16_ 反走樣_7_區域邊界的反走樣
區域邊界的反走樣 直線的反走樣概念也可以用於區域的邊界，從而消除其鋸齒形的外貌。我們可以將這種程式加加入到掃描線演算法中，在生成區域時來平滑區域輪廓。假如系統具有允許畫素重定位的功能，那麼就可以將邊界畫素位置調整到更靠近區域邊界來實現對區域邊界的平滑處理。
計算機圖形學（三）掃描線多邊形填充演算法講解與原始碼
如果喜歡轉載請標明出處： 並非菜鳥菜鳥的部落格 在這裡先說下演算法的實現過程 本人覺得這個演算法實現起來還是有點難度的！很多人都不願意去看太多描述性的文字，所以對這個演算法的過程是什麼大概也不知道，那麼我在這裡簡要的說一些！ 演算法實現過程中應用兩個資料結構：
計算機圖形學（一）
概念： 研究通過計算機將資料轉換為圖形並在專門顯示裝置上顯示的原理方法和技術的學科 高質量的計算機圖形離不開高效能的計算機圖形硬體裝置。一個圖形系統通常是由圖形處理器，圖形輸入裝置和輸出裝置構成。 圖形顯示裝置* 圖形的輸出包括圖形的顯示和繪製。圖形的顯
MFC計算機圖形學（3）
之前我們已經可以畫出直線和曲線了。但是演算法雖容易理解，但是複雜度高，今天就介紹比較流行的DDA畫線法，還有，對滑鼠進行事件有所響應，即，在畫板上，滑鼠左鍵單擊，移動至另外一個地方鬆開，此時在這兩個點之間畫一條線。 DDA畫線 演算法程式碼 void
計算機圖形學（六）多邊形裁剪Sutherland-Hodgeman演算法講解與原始碼
因為最近CSDN上傳資源出現問題，無法上傳，等可以上傳之後再給出下載地址。 原始碼下載：點我下載 首先講一下演算法的原理： Sutherland-Hodgeman演算法： 基本思想是一次用視窗的一條邊裁剪多邊形。 考慮視窗的一條邊以及延長線構成的裁剪線，該線把平面分成兩
【影象處理】OpenCV+Python影象處理入門教程（四）幾何變換
這篇隨筆介紹使用OpenCV進行影象處理的第四章 幾何變換。 4 幾何變換 影象的幾何變換是指將一幅影象對映到另一幅影象內。有縮放、翻轉、仿射變換、透視、重對映等操作。 4.1
計算機圖形學（二）輸出圖元_3_畫線算法_2_DDA算法
通過 程序 之間 tro 取整 xen git 方程 class DDA算法? ? ? ? 數字微分分析儀(digital differential analyzer, DDA)方法是一種線段掃描轉換算法。基於使用等式(3
計算機圖形學（第2版 於萬波 於碩 編著）第45頁的Bresenham算法有錯誤
str mage mov 步長 分享圖片 圖片 方法總結 tro 計算 計算機圖形學（第2版 於萬波 於碩 編著）第45頁的Bresenham算法有錯誤： 書上本來要寫的是以x為階越步長的方法，但是他寫的是用一部分y為階越步長的方法（其實也寫的不對），最後以x為階越
計算機圖形學（三種畫線算法）
直線 情況 算法 n) src 隨著 多邊形 取整 兩個 第二章：光柵圖形學算法 1、光柵顯示器：光柵掃描式圖形顯示器簡稱光柵顯示器，是畫點設備，可看作是一個點陣單元發生器，並可控制每個點陣單元的亮度 2、由來：隨著光柵顯示器的出現，為了在計算機上處理、顯示圖形，需要發展一