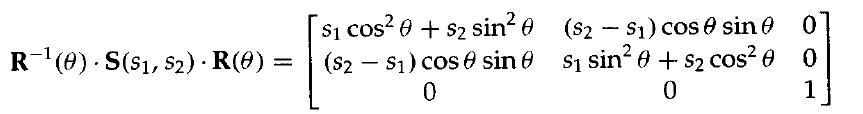計算機圖形學(四)幾何變換_4_二維複合變換(上)
阿新 • • 發佈:2019-01-10
二維複合變換
利用矩陣表示式,可以通過計算單個變換的矩陣乘積,將任意的變換序列組成複合變換矩陣(compsite transformation matrix)。形成變換矩陣的乘積經常稱為矩陣的合併(concatenation)或複合(compsistion)。由於一個座標位置用齊次列矩陣表示,我們必須用表達任一變換次序的矩陣前乘該列矩陣。由於場景中許多位置用相同的順序變換,先將所有變換矩陣相乘形成一個複合矩陣將是高效率的方法。因此,如果我們要對點位置P經行兩次變換,變換後的位置將用下式計算:
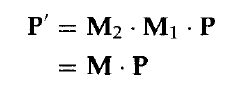 該座標位置使用矩陣M來變換,而不是單獨地先用M1然後M2來變換。
該座標位置使用矩陣M來變換,而不是單獨地先用M1然後M2來變換。
4.1 複合二維平移
假如將兩個連續的平移向量(t1x
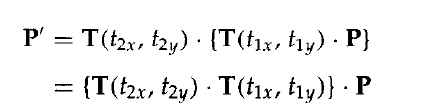 其中,P和P’表示為三元素,齊次座標的列表向量。我們可以計算兩個相關的矩陣乘積來檢驗這個結果。同樣,這個平移序列的複合變換矩陣為:
其中,P和P’表示為三元素,齊次座標的列表向量。我們可以計算兩個相關的矩陣乘積來檢驗這個結果。同樣,這個平移序列的複合變換矩陣為:
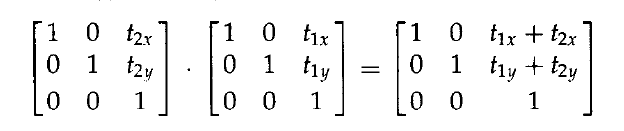
或:
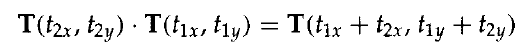 這表示兩個連續平移是相加的。
這表示兩個連續平移是相加的。
4.2 複合二維旋轉
應用於P的兩個連續旋轉產生的變換為:
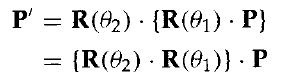 通過兩個旋轉矩陣相乘,我們可以證明兩個連續旋轉是相加的
通過兩個旋轉矩陣相乘,我們可以證明兩個連續旋轉是相加的
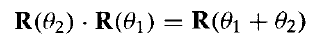
因此,點旋轉的最後座標可以使用複合變換矩陣計算為:
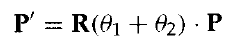 4.3複合二維縮放
4.3複合二維縮放
合併兩個連續的二維縮放操作的變換矩陣,生成如下的複合縮放矩陣:

或

這種情況下的結果矩陣表明,連續縮放操作是相乘的,假如我們要連續兩次將物件尺寸放大3倍,那麼其最後的尺寸將是原來尺寸的9倍。
4.4通用二維基準點旋轉
當圖形軟體包僅提供繞座標系原點旋轉函式時,我們可通過完成下列平移-旋轉-平移操作序列來實現繞任何選定的基準點(xr, yr)的旋轉。
1.平移物件使基準點位置移動到座標原點;
2.繞座標原點旋轉;
3.平移物件使基準點回到其原始位置
這個變換序列如圖所示。利用矩陣合併可以得到該序列的複合變換矩陣方程1:
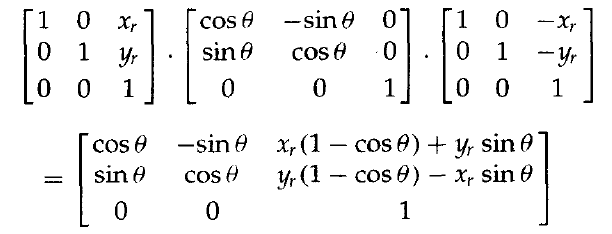
可以使用下列形式表示:
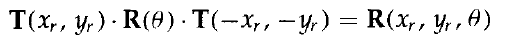
其中,T(-xr,-yr)= T-1(xr,yr)。通常,可以將圖形庫中的旋轉函式設計成先接收基準點座標引數及旋轉角,然後自動生成方程1的旋轉矩陣。

4.5 通用二維基準點縮放
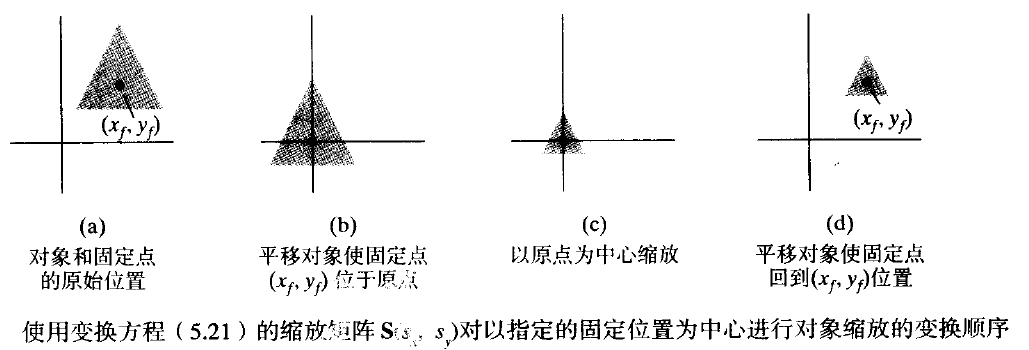
只有相對於座標原點縮放的縮放函式時,下圖中給出了關於任意選擇的基準位置(
1.平移物件使
2.對於座標原點經行縮放;
3.使用步驟1的反向平移將物件返回到原始位置。
將這三個操作的矩陣合併,就可以產生所需的縮放矩陣:

或:
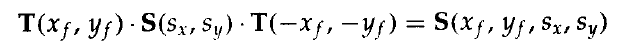
該變換在提供接收基準點座標的縮放函式的系統中自動生成。
4.6 通用二維定向縮放
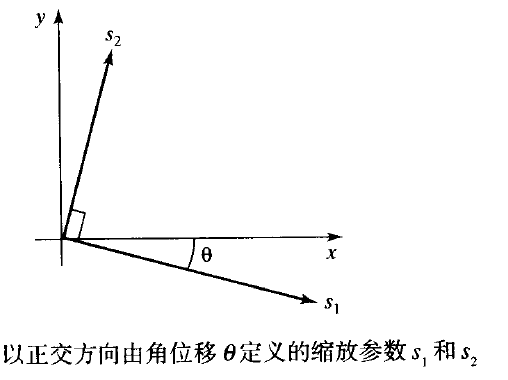
引數Sx和Sy沿x和y方向縮放物件,可以通過在應用縮放變換之前,將物件所希望的縮放方向旋轉到與座標一致而在其他方向上縮放物件。假如我們要在下圖所示的方向上使用引數S1和S2指定的值作為縮放係數。為了完成這種縮放而不改變物件方向,我們首先完成旋轉操作,使s1和s2的方向分別與x和y軸重合。然後應用縮放變換S(s1,s2),再經行反向旋轉以回到其原始位置。從這三個變換的乘積得到的複合矩陣2為:
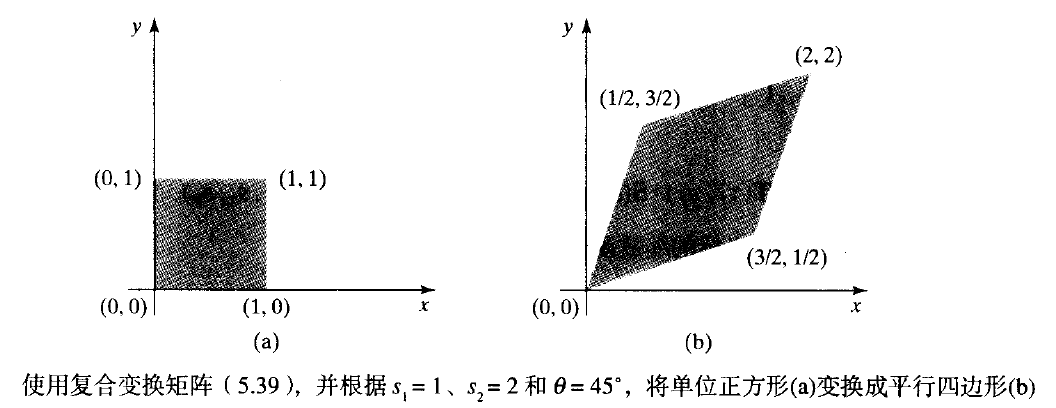
作為縮放變換的一個例子,通過沿(0,0)到(1, 1)的對角線將單位正方形拉長,使其轉換成平行四邊形(參見下圖 )。我們使用引數θ= 45度將對角線旋轉到y軸,並按s1 = 1和s2 = 2將其長度加倍,然後再旋轉使對角線回到原來的位置。
在複合矩陣2,假設縮放是相對原點完成的,可以將這個縮放操作推進一步並與平移操作合併,從而使複合矩陣包含為指定的固定位置進行縮放的引數。
利用矩陣表示式,可以通過計算單個變換的矩陣乘積,將任意的變換序列組成複合變換矩陣(compsite transformation matrix)。形成變換矩陣的乘積經常稱為矩陣的合併(concatenation)或複合(compsistion)。由於一個座標位置用齊次列矩陣表示,我們必須用表達任一變換次序的矩陣前乘該列矩陣。由於場景中許多位置用相同的順序變換,先將所有變換矩陣相乘形成一個複合矩陣將是高效率的方法。因此,如果我們要對點位置P經行兩次變換,變換後的位置將用下式計算:
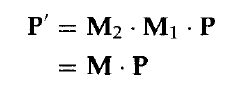 該座標位置使用矩陣M來變換,而不是單獨地先用M1然後M2來變換。
該座標位置使用矩陣M來變換,而不是單獨地先用M1然後M2來變換。4.1 複合二維平移
假如將兩個連續的平移向量(t1x
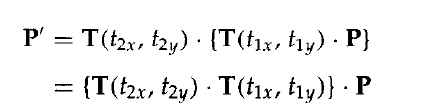 其中,P和P’表示為三元素,齊次座標的列表向量。我們可以計算兩個相關的矩陣乘積來檢驗這個結果。同樣,這個平移序列的複合變換矩陣為:
其中,P和P’表示為三元素,齊次座標的列表向量。我們可以計算兩個相關的矩陣乘積來檢驗這個結果。同樣,這個平移序列的複合變換矩陣為: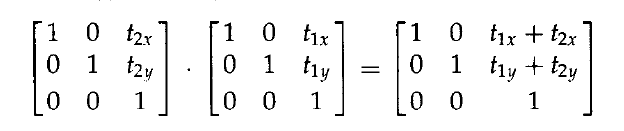
或:
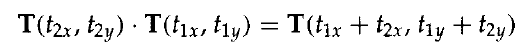 這表示兩個連續平移是相加的。
這表示兩個連續平移是相加的。4.2 複合二維旋轉
應用於P的兩個連續旋轉產生的變換為:
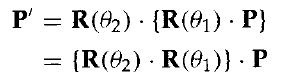 通過兩個旋轉矩陣相乘,我們可以證明兩個連續旋轉是相加的
通過兩個旋轉矩陣相乘,我們可以證明兩個連續旋轉是相加的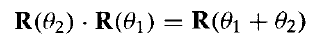
因此,點旋轉的最後座標可以使用複合變換矩陣計算為:
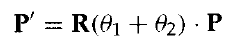 4.3複合二維縮放
4.3複合二維縮放合併兩個連續的二維縮放操作的變換矩陣,生成如下的複合縮放矩陣:

或

這種情況下的結果矩陣表明,連續縮放操作是相乘的,假如我們要連續兩次將物件尺寸放大3倍,那麼其最後的尺寸將是原來尺寸的9倍。
4.4通用二維基準點旋轉
當圖形軟體包僅提供繞座標系原點旋轉函式時,我們可通過完成下列平移-旋轉-平移操作序列來實現繞任何選定的基準點(xr, yr)的旋轉。
1.平移物件使基準點位置移動到座標原點;
2.繞座標原點旋轉;
3.平移物件使基準點回到其原始位置
這個變換序列如圖所示。利用矩陣合併可以得到該序列的複合變換矩陣方程1:
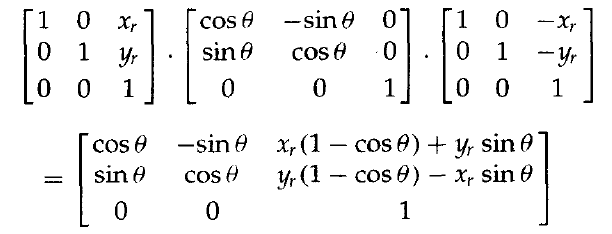
可以使用下列形式表示:
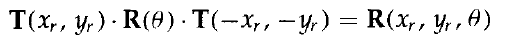
其中,T(-xr,-yr)= T-1(xr,yr)。通常,可以將圖形庫中的旋轉函式設計成先接收基準點座標引數及旋轉角,然後自動生成方程1的旋轉矩陣。

4.5 通用二維基準點縮放
只有相對於座標原點縮放的縮放函式時,下圖中給出了關於任意選擇的基準位置(
1.平移物件使
2.對於座標原點經行縮放;
3.使用步驟1的反向平移將物件返回到原始位置。
將這三個操作的矩陣合併,就可以產生所需的縮放矩陣:

或:
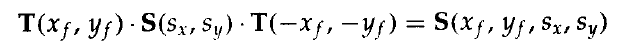
該變換在提供接收基準點座標的縮放函式的系統中自動生成。

4.6 通用二維定向縮放
引數Sx和Sy沿x和y方向縮放物件,可以通過在應用縮放變換之前,將物件所希望的縮放方向旋轉到與座標一致而在其他方向上縮放物件。假如我們要在下圖所示的方向上使用引數S1和S2指定的值作為縮放係數。為了完成這種縮放而不改變物件方向,我們首先完成旋轉操作,使s1和s2的方向分別與x和y軸重合。然後應用縮放變換S(s1,s2),再經行反向旋轉以回到其原始位置。從這三個變換的乘積得到的複合矩陣2為:
作為縮放變換的一個例子,通過沿(0,0)到(1, 1)的對角線將單位正方形拉長,使其轉換成平行四邊形(參見下圖 )。我們使用引數θ= 45度將對角線旋轉到y軸,並按s1 = 1和s2 = 2將其長度加倍,然後再旋轉使對角線回到原來的位置。
在複合矩陣2,假設縮放是相對原點完成的,可以將這個縮放操作推進一步並與平移操作合併,從而使複合矩陣包含為指定的固定位置進行縮放的引數。