圖的最短路徑演算法(Dijkstra,Floyd)的實現
阿新 • • 發佈:2019-01-02
從某個源點到其餘各頂點的最短路徑
迪杰特斯拉演算法
Dijkstra(迪傑斯特拉)演算法是典型的單源最短路徑演算法,用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件,直到擴充套件到終點為止。
演算法步驟如下:
- 初使時令 S={V0},T={其餘頂點},T中頂點對應的距離值
若存在,d(V0,Vi)為弧上的權值,
若不存在,d(V0,Vi)為∝- 從T中選取一個其距離值為最小的頂點W且不在S中,加入S
- 對其餘T中頂點的距離值進行修改:若加進W作中間頂點,從V0到Vi的
距離值縮短,則修改此距離值重複上述步驟2、3,直到S中包含所有頂點,即W=Vi為止
完整C++程式碼:
#include <iostream>
#include <climits>
using namespace std;
#define MAX_VERTEX_NUM 20 // 頂點數量上限
typedef char VerType; // 頂點結構 , 頂點的字母名稱
typedef int ArcType; // 邊的結構 , 權值
typedef enum {DG, UDG} GKind; // 圖型別,{有向圖,無向圖}
// 圖的儲存結構
typedef struct
{
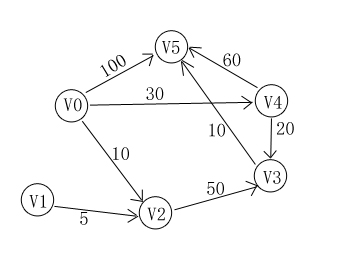
int verNum, arcNum; // 頂點數量, 邊數量 程式碼中的圖為:
執行結果:
每一對頂點之間的最短路徑
弗洛伊德演算法
Floyd演算法(Floyd-Warshall algorithm)又稱為弗洛伊德演算法、插點法,是解決給定的加權圖中頂點間的最短路徑的一種演算法,可以正確處理有向圖或負權的最短路徑問題,同時也被用於計算有向圖的傳遞閉包。
演算法步驟如下:
1,從任意一條單邊路徑開始。所有兩點之間的距離是邊的權,如果兩點之間沒有邊相連,則權為無窮大。
2,對於每一對頂點u和v,看看是否存在一個頂點w使得從u到w再到v比已知的路徑更短。如果是更新它。
把圖用鄰接矩陣G表示出來,如果從Vi到Vj有路可達,則G[i,j]=d,d表示該路的長度;否則G[i,j]=無窮大。定義一個矩陣D用來記錄所插入點的資訊,D[i,j]表示從Vi到Vj需要經過的點,初始化D[i,j]=j。把各個頂點插入圖中,比較插點後的距離與原來的距離,G[i,j]=min(G[i,j],G[i,k]+G[k,j]),如果G[i,j]的值變小,則D[i,j]=k。在G中包含有兩點之間最短道路的資訊,而在D中則包含了最短通路徑的資訊。
比如,要尋找從V5到V1的路徑。根據D,假如D(5,1)=3則說明從V5到V1經過V3,路徑為{V5,V3,V1},如果D(5,3)=3,說明V5與V3直接相連,如果D(3,1)=1,說明V3與V1直接相連。
完整C++程式碼:
#include <iostream>
#include <climits>
#include <iomanip>
using namespace std;
#define MAX_VERTEX_NUM 20 // 頂點數量上限
typedef char VerType; // 頂點結構 , 頂點的字母名稱
typedef int ArcType; // 邊的結構 , 權值
typedef enum {DG, UDG} GKind; // 圖型別,{有向圖,無向圖}
// 圖的儲存結構
typedef struct
{
int verNum, arcNum; // 頂點數量, 邊數量
GKind kind; // 圖型別
VerType vertex[MAX_VERTEX_NUM]; //頂點
ArcType arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //邊
}Graph;
void CreateGraphByArray(Graph &G); // 建立圖G (通過預定義的陣列)
int VertexLoc(const Graph &G, const VerType &v); // 獲取頂點v在圖G中的位置
void ShortestPath_Floyd(Graph &G); // 最短路徑演算法 (弗洛伊德演算法)
int main()
{
Graph G;
CreateGraphByArray(G);
ShortestPath_Floyd(G);
return 0;
}
void CreateGraphByArray(Graph &G)
{
G.kind = DG;
const int vn = 4;
VerType V[vn + 1] = {"0123"};
const int en = 8;
VerType V1[en + 1] = {"00112223"};
VerType V2[en + 1] = {"13323012"};
ArcType E[en] = {1,4,2,9,8,3,5,6};
// 輸入頂點
G.verNum = vn;
for(int i = 0; i < G.verNum; ++ i){
G.vertex[i] = V[i];
}
// 初始化鄰接矩陣
for(int vi = 0; vi < G.verNum; ++ vi){
for(int vj = 0; vj < G.verNum; ++ vj){
G.arcs[vi][vj] = INT_MAX;
}
}
// 輸入邊
G.arcNum = en;
for(int i = 0; i < G.arcNum; ++ i){
VerType &v1 = V1[i], &v2 = V2[i];
ArcType &e = E[i];
int vi = VertexLoc(G, v1), vj = VertexLoc(G, v2);
if(vi == G.verNum || vj == G.verNum){
continue;
}
if(UDG == G.kind){
G.arcs[vi][vj] = G.arcs[vj][vi] = e;
}else{
G.arcs[vi][vj] = e;
}
}
}
int VertexLoc(const Graph &G, const VerType &v)
{
for(int i = 0; i < G.verNum; ++ i){
if(G.vertex[i] == v){
return i;
}
}
return G.verNum;
}
void ShortestPath_Floyd(Graph &G)
{
const int N = G.verNum;
int Path[N][N]; //表示vi和vj之間的最短路上的前驅頂點
long long D[N][N]; //表示vi和vj之間的最短路徑長度
for(int i = 0; i < N ; ++ i){
for(int j = 0; j < N; ++ j){
D[i][j] = G.arcs[i][j];
Path[i][j] = D[i][j] != INT_MAX ? i : -1;
}
}
for(int k = 0; k < N; ++ k){
for(int i = 0; i < N; ++ i){
for(int j = 0; j < N; ++ j){
if(D[i][k] + D[k][j] < D[i][j]){
D[i][j] = D[i][k] + D[k][j];
Path[i][j] = Path[k][j];
}
}
}
}
/* 輸出每對最短路徑 */
for(int i = 0; i < N; ++ i){
for(int j = 0; j < N; ++ j){
cout << G.vertex[i] << "→" << G.vertex[j] << ": " << G.vertex[j];
for(int vi = Path[i][j]; vi != i; vi = Path[i][vi]){
cout << "←" << G.vertex[vi];
}
cout << "←" << G.vertex[i] << " (" << D[i][j] << ")" << endl;
}
}
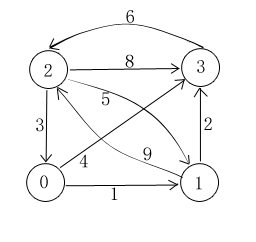
}對於下面的圖:
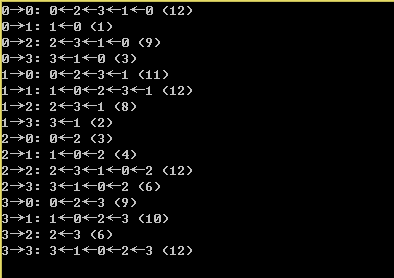
執行結果: